Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonality in Eigenvectors
Unlock Audio Lesson
Today, let's explore the concept of orthogonality specifically in the context of eigenvectors of real symmetric matrices. Can anyone remind us what makes a matrix symmetric?
Isn't a symmetric matrix one where the transpose equals itself? So A equals A^T?
Exactly right! Now, if we consider eigenvectors from a symmetric matrix, what do you think we know about those eigenvectors?
I think they might be orthogonal if their eigenvalues are distinct?
Good job! That's the key point. Eigenvectors corresponding to distinct eigenvalues of a real symmetric matrix are indeed orthogonal.
Can you explain what orthogonal means in this context?
Of course! Orthogonality means the dot product of two vectors is zero, symbolically expressed as $$x_1^T x_2 = 0$$ for distinct eigenvectors. This means the direction of these vectors are at right angles to each other.
How does this property help us in engineering?
Excellent question! In modal analysis, having orthogonal eigenvectors simplifies calculations significantly, especially when analyzing dynamic systems.
Today we learned that distinct eigenvectors of a real symmetric matrix exhibit orthogonality. This property facilitates easier calculations in modal analysis and thus plays a vital role in engineering.
Application of Orthogonality in Engineering
Unlock Audio Lesson
Now that we understand orthogonality, let’s discuss its applications. How do you think this property assists in modal analysis?
Could it help reduce computational complexity?
Exactly! It allows us to decouple modes of vibration, making calculations more efficient. Suppose a structure has multiple mode shapes; can anyone explain how to represent them using eigenvectors?
I believe we can arrange them in a matrix and use them to analyze vibrations?
That's spot on! The columns of the modal matrix represent these orthogonal eigenvectors. Would anyone like to give a real-world example of where this is applied?
In bridge construction, I think engineers need to analyze how the bridge vibrates under load, right?
Exactly right! Engineers leverage these orthogonal eigenvectors to determine natural frequencies and ensure structural safety.
In conclusion, we discussed how orthogonality of eigenvectors facilitates modal analysis in engineering, improving both the accuracy and efficiency of structural assessments.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In the context of a real symmetric matrix, the eigenvectors associated with distinct eigenvalues exhibit orthogonality, meaning their dot product equals zero. This property is especially useful in modal analysis, where orthogonal mode shapes allow for easier computations.
Detailed
Orthogonality of Eigenvectors
In this section, we delve into the important property of eigenvectors associated with real symmetric matrices. When a matrix A is real and symmetric, it guarantees that its eigenvectors linked to distinct eigenvalues are orthogonal. This mathematical conclusion plays a pivotal role in various applications, including modal analysis in civil engineering. The orthogonality, represented as
$$x_1^T x_2 = 0$$
for eigenvectors $$x_1$$ and $$x_2$$ with distinct eigenvalues $$ 0b$$ and $$ 0b$$ respectively, indicates a significant simplification in the calculations involved in structural analysis and vibration analysis. By leveraging this orthogonality, engineers can streamline their computations for evaluating system behaviors under dynamic loading conditions.
Youtube Videos
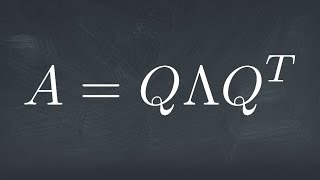
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Orthogonality in Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If A is a real symmetric matrix, then:
• Eigenvectors corresponding to distinct eigenvalues are orthogonal.
Detailed Explanation
This statement establishes a fundamental property of eigenvectors associated with real symmetric matrices. 'A is a real symmetric matrix' means that the matrix is equal to its transpose. When eigenvectors correspond to distinct eigenvalues, it means that each eigenvalue is unique. The term 'orthogonal' indicates that these eigenvectors are at right angles to each other in a multi-dimensional space. This property is crucial in various applications, such as simplifying calculations in modal analysis, where eigenvectors represent different modes of vibrations or oscillations.
Examples & Analogies
Think of the orthogonality of eigenvectors like the axis of a coordinate system. For instance, the x-axis and y-axis are orthogonal, meaning they are at right angles to each other. Just like these axes can represent different dimensions in space without interfering with each other, orthogonal eigenvectors can represent independent modes of operation in a system without overlap.
Significance of Orthogonality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This orthogonality is useful in modal analysis, where orthogonal mode shapes simplify calculations.
Detailed Explanation
Orthogonality simplifies the mathematical representation and computation of systems undergoing oscillations, such as in structural engineering. In modal analysis, which involves studying the natural modes of vibration of structures, orthogonality allows for the separation of these modes. Because the modes are distinct and independent, they can be analyzed individually without complicating interactions, making it easier to compute responses under various loading conditions.
Examples & Analogies
Consider a musical orchestra, where each musician plays a different instrument. Each instrument contributes its unique sound without interfering with others. In the same way, orthogonal eigenvectors act like individual musicians contributing to the overall performance of a structure's response to dynamic loads, allowing each mode's effects to be analyzed separately. This separation leads to more manageable calculations and clearer insights into the system's behavior.
Mathematical Representation of Orthogonality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A=AT, and x1, x2 be eigenvectors with distinct eigenvalues λ1, λ2, then:
1
xT1 x2 = 0
Detailed Explanation
This equation mathematically expresses the condition for orthogonality. Here, x1 and x2 are eigenvectors of the symmetric matrix A, and T denotes the transpose. The product xT1 x2 equals zero indicates that when we take the dot product of the two vectors, there is no overlap in their directionality, confirming their orthogonality. This property can be used to verify that the eigenvectors found from a real symmetric matrix correctly represent independent directions in the associated vector space.
Examples & Analogies
Imagine two roads that run perpendicular to each other, like an intersection in a city. The paths of the roads represent the directions of the eigenvectors. As you drive along one road, you have no influence on the other road; they remain independent of each other. Similarly, the mathematical expression xT1 x2 = 0 confirms that eigenvectors, like these roads, do not affect each other when subjected to different conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector: A vector that is only scaled by a matrix transformation.
-
Eigenvalue: A scalar associated with an eigenvector indicating the scaling factor.
-
Orthogonality: The condition that distinct eigenvectors of a real symmetric matrix yield a dot product of zero.
-
Symmetric Matrix: A matrix that is equal to its transpose, providing eigenvectors that are orthogonal.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a symmetrical frame structure, distinct mode shapes can be represented as orthogonal eigenvectors, allowing for easier analysis of vibrations.
-
In dynamical systems, orthogonal eigenvectors reduce the complexity of solving differential equations by allowing decoupled analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvectors relate in separation, distinct pairs show no correlation.
📖 Fascinating Stories
-
Imagine two dancers performing at right angles to each other, their movements perfectly aligned with the concept of orthogonality.
🧠 Other Memory Gems
-
O.E.S. - Orthogonal Eigenvectors are Special.
🎯 Super Acronyms
S.O.E. - Symmetric matrices offer Eigenvectors that are Orthogonal.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonality
Definition:
A property of vectors where their dot product equals zero, indicating that they are perpendicular to each other.
-
Term: Eigenvector
Definition:
A non-zero vector that is scaled by a matrix during the transformation, defined by the equation Ax = λx.
-
Term: Eigenvalue
Definition:
A scalar that indicates how much an eigenvector is stretched or compressed during a matrix transformation.
-
Term: Symmetric Matrix
Definition:
A matrix that is equal to its transpose, denoted as A = A^T.
-
Term: Modal Analysis
Definition:
An analysis technique used to study the dynamic behavior of structures under various loading conditions.