Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Buckling
Unlock Audio Lesson
Today, we're going to explore the concept of buckling in stability studies. Buckling is a failure mode under compressive load where structures like columns can dramatically deform.
What causes a column to buckle?
Great question! When the axial load on a column exceeds a certain critical point, it can no longer maintain its straight shape and can bend or buckle instead.
How is the critical load determined?
The critical load is determined using eigenvalues. Specifically, the smallest eigenvalue corresponds to the critical load at which buckling occurs.
What does the eigenvector represent in this context?
The eigenvector represents the buckled shape of the structure. It shows how the structure deforms when buckling occurs.
So, each critical load has a corresponding shape?
Exactly! Each eigenvalue is linked to a specific deformation pattern, known as a buckling mode shape.
To summarize, buckling is essentially a change in shape due to excessive loading, characterized by eigenvalues and their corresponding eigenvectors.
Mathematical Framework
Unlock Audio Lesson
Now let's break down the math behind buckling. The governing equation for a beam-column is represented as $$ EI \frac{d^4y}{dx^4} + P = 0 $$.
What are EI and P in this equation?
EI denotes the flexural rigidity of the column, while P is the axial load applied to it. Together, they describe the column's resistance to bending.
How do we move from this equation to eigenvalues?
We reformulate the buckling problem into an eigenvalue problem, leading us to $$ (K - \lambda G)x = 0 $$, where K is the stiffness matrix and G represents the geometric stiffness matrix.
So λ is the eigenvalue?
Correct! Here, λ corresponds to the critical load multiplier, and x gives us the mode shapes or buckled shapes.
Is this transformation important for practical analysis?
Absolutely! It allows engineers to leverage mathematical models to predict stability and operational capabilities of structures.
In summary, understanding the mathematical relationships through these eigenvalue problems enables engineers to effectively analyze and mitigate buckling.
Application in Engineering
Unlock Audio Lesson
Let's talk about how engineers apply these concepts in real life. Eigenvalues and eigenvectors are crucial in predicting structural failures.
Can you give an example?
Sure! In designing skyscrapers, engineers must consider how the columns will behave under wind loads. Using eigenvalue analysis helps determine when and where buckling might occur.
So this analysis can save lives?
Exactly! It ensures safety and stability in tall structures where failure could have catastrophic consequences.
What tools do engineers use for this analysis?
Common tools include finite element software like ANSYS, which can calculate these eigenvalues and mode shapes efficiently.
What about more complex structures like bridges?
For complex structures, modal analysis helps in enhancing design robustness and resilience against unexpected loads, using eigenvector analysis for optimization.
To wrap up, using eigenvectors and eigenvalues in engineering practices allows for considerable improvements in stability assessments, ultimately leading to safer structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvectors play a vital role in determining the critical load at which columns buckle under axial loads. By framing this within an eigenvalue problem, engineers can identify the smallest eigenvalue corresponding to the critical load and the eigenvector that represents the buckled shape of the column, thus helping in structural analysis.
Detailed
Stability and Buckling
In civil engineering, stability and buckling are critical considerations when analyzing structural components, especially columns. This section delves into how eigenvalues and eigenvectors relate to these phenomena.
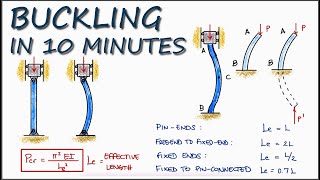
Buckling occurs when a structural element becomes unstable under an axial load, leading to failure. The critical load at which buckling occurs is expressed as an eigenvalue problem, where the smallest eigenvalue corresponds to this critical load. The associated eigenvector provides the shape that the structure deforms into when it buckles.
The governing differential equation governing buckling for a beam-column can be expressed as:
$$ EI \frac{d^4y}{dx^4} + P = 0 $$
where:
- EI is the flexural rigidity
- P is the axial load.
In matrix structural analysis, the problem transforms into a discrete eigenvalue problem represented by:
$$ (K - \lambda G)x = 0 $$
where K denotes the stiffness matrix, G signifies the geometric stiffness matrix, \lambda represents the load multiplier or eigenvalue, and x indicates the buckling mode shape. Understanding these relationships helps engineers predict when a structure may fail under specific loading conditions, leading to safer and more effective designs.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Buckling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Buckling of columns under axial loads leads to an eigenvalue problem where the critical load corresponds to the smallest eigenvalue and the buckled shape is the eigenvector.
Detailed Explanation
When a column is subjected to an axial load, it may start to bend or buckle rather than just compress. The load at which this occurs is called the critical load. This phenomenon can be understood through the lens of eigenvalues and eigenvectors. In this context, the smallest eigenvalue represents the critical load, while the corresponding eigenvector describes the shape that the column will take when it buckles. Essentially, we use these mathematical concepts to predict how a structure will fail when under certain loads, allowing engineers to design safer buildings.
Examples & Analogies
Imagine a tower made of flexible plastic. If you gently push down on the top, it might bend a little. But if you push down harder, at some point it will suddenly bend a lot more dramatically—this point is analogous to the critical load in buckling. Just as understanding the bending shape helps us predict what will happen to the tower, eigenvectors help engineers understand how columns will behave under heavy loads.
Eigenvalue Problem in Buckling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In matrix structural analysis, this becomes a discrete eigenvalue problem: (K−λG)x=0 Where: K: stiffness matrix, G: geometric stiffness matrix, λ: load multiplier (eigenvalue), x: buckling mode shape.
Detailed Explanation
When analyzing the stability of structures, especially those like columns that may buckle, engineers often set up an eigenvalue problem in matrix form. Here, K represents the stiffness of the structure, which quantifies how much it resists deformation or bending. In contrast, G represents the geometric stiffness, which accounts for changes in the structure's geometry under load. The equation (K−λG)x=0 allows us to determine the eigenvalues (λ), which help identify the critical loads, and the eigenvectors (x), which represent the shapes that the structure will take when it buckles. Solving this equation gives engineers the necessary information to ensure that structures can withstand intended loads without failing.
Examples & Analogies
Think of K as a tightrope walker using a stiff pole for balance. The stiffer the pole, the more resistance it provides against bending. If the tightrope is balanced perfectly, that's like finding the right load where a structure won't buckle. But if there is too much weight (like λ being too large), the pole will bend in a specific way (the eigenvector) that might cause the walker to fall. By studying these 'balance points' in structures, engineers can prevent 'falls' in real-life buildings.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buckling: The instability of a structure under axial loads leading to deformation.
-
Critical Load: The load at which structures like columns buckle.
-
Eigenvalues: Scalar values that correlate with the critical loads.
-
Eigenvectors: Vectors that represent the mode shapes of buckling.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A steel column under axial load that buckles at a critical load, represented by its smallest eigenvalue.
-
A bridge's response to wind load analyzed using eigenvalue methods to prevent buckling.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the load’s too great, watch structures bend low; buckling occurs, and away they'll go!
📖 Fascinating Stories
-
Imagine a tall tower that swayed in the wind. Engineers calculated its limits; they used eigenvalues to avoid a grim end when it buckled under stress.
🧠 Other Memory Gems
-
B.E.C.K. for Buckling: B for Buckle, E for Eigenvalue, C for Critical Load, K for Stiffness matrix.
🎯 Super Acronyms
B.E.C.K
- B: (Buckle)
- E: (Eigenvalue)
- C: (Critical load)
- K: (Stiffness matrix)
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buckling
Definition:
A failure mode of structures under axial load characterized by sudden lateral deformation.
-
Term: Eigenvalue
Definition:
A scalar value that indicates the factor by which a corresponding eigenvector is scaled during a linear transformation.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only by a scalar factor when acted upon by a matrix.
-
Term: Critical Load
Definition:
The axial load at which a column becomes unstable and buckles.
-
Term: Stiffness Matrix
Definition:
A matrix that describes the stiffness of a structure and its resistance to deformation.
-
Term: Geometric Stiffness Matrix
Definition:
A matrix that accounts for the geometric effects on stiffness, especially under axial loads.