Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Generalized Eigenvectors
Unlock Audio Lesson
Today we are diving into generalized eigenvectors. Can anyone tell me what an eigenvector is?
An eigenvector is a vector that only gets scaled when multiplied by a matrix.
Exactly! But sometimes, matrices have repeated eigenvalues and aren’t diagonalizable. This is where generalized eigenvectors come into play. Who can tell me what a generalized eigenvector does?
Is it a vector that satisfies `(A−λI)^k x=0` for some k?
Correct! And does anyone know why this is important in engineering?
Because it helps analyze systems that are not conservative?
That's right! Generalized eigenvectors are crucial for understanding damped vibration problems and improve our structural analysis. Let's summarize: generalized eigenvectors allow us to handle matrices that wouldn't otherwise be the full basis of eigenvectors.
Generalized Eigenvector Concepts
Unlock Audio Lesson
Now, let's explore the properties of generalized eigenvectors. When we say an eigenvector is of rank k, what does that really mean?
It refers to how many times we need to apply the operator to reach zero.
Exactly! The higher the rank, the more times we must apply the matrix transformation. This is critical when forming the Jordan canonical form. Can anyone explain what that is?
It’s a way to bring a matrix into a block diagonal form even if it can't be diagonalized.
Right! It generalizes diagonalization to include cases of repeated eigenvalues. This is particularly useful in engineering applications. Remember, certain damping systems require these concepts for effective analysis.
So, in damped systems, generalized eigenvectors help us understand the behavior better?
Absolutely! To recap, generalized eigenvectors and the Jordan form are essential for dealing with more complex systems in our field.
Applications of Generalized Eigenvectors
Unlock Audio Lesson
Let's link generalized eigenvectors back to our work. Why might these be applicable in civil engineering?
They help with stability analysis in structures that have repeating modes?
Exactly! Structures like bridges can have non-conservative systems, and generalized eigenvectors can predict how they behave under loads.
And they help in damping vibrations, right?
Indeed! The understanding of how vibrations operate under conditions is crucial for designing efficient and stable structures. Who can summarize what we've learned today about generalized eigenvectors?
Generalized eigenvectors help us analyze systems with repeated eigenvalues and cannot be diagonalized, improving our structural analysis, especially for damping-related problems.
Fantastic summary! Always remember how these concepts link back to practical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses generalized eigenvectors for matrices with repeated eigenvalues that do not have a full basis of eigenvectors, introducing the concept of rank and its implications in the Jordan canonical form and applications in civil engineering.
Detailed
Detailed Summary
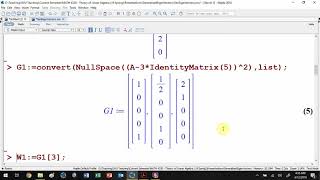
In linear algebra, generalized eigenvectors extend the concept of eigenvectors for matrices that have repeated eigenvalues but do not yield a complete set of linearly independent eigenvectors. Specifically, a generalized eigenvector of rank k satisfies the equation
(A−λI)^k x=0,
while the previous rank
(A−λI)^{k−1} x≠0 holds for the same vector. This framework helps form a Jordan canonical form, which generalizes diagonalization, allowing for matrices that cannot be directly diagonalized.
Applications of generalized eigenvectors are particularly significant in civil engineering, especially when dealing with non-conservative systems or damped vibration problems where the governing matrices lack symmetry and do not permit traditional diagonalization. In these scenarios, understanding the implications of generalized eigenvectors can improve analysis in structural dynamics, aiding in the design and evaluation of engineering systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Generalized Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In some cases, a matrix may not have enough linearly independent eigenvectors to be diagonalizable. This happens when it has repeated eigenvalues but lacks a full basis of eigenvectors. In such cases, we use generalized eigenvectors.
Detailed Explanation
Generalized eigenvectors serve as a solution when a matrix cannot be fully diagonalized due to a lack of independent eigenvectors. This situation often arises with matrices that have repeated eigenvalues. For example, if a matrix has eigenvalue λ that is repeated multiple times but does not provide enough distinct eigenvectors, we cannot simply use standard eigenvectors to describe the matrix's behavior. Instead, generalized eigenvectors are introduced to extend our basis and help us understand the matrix's structure better.
Examples & Analogies
Imagine trying to fill a jar with different types of marbles but realizing you have a limited amount of certain kinds, such as blue marbles. To ensure the jar looks full, you might use decorative stones (generalized eigenvectors) to fill in the gaps where marbles alone cannot do the job. This way, you create a visually complete representation, just like how generalized eigenvectors help us understand matrices that can't be represented solely by traditional eigenvectors.
Mathematical Definition of Generalized Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A generalized eigenvector of rank k satisfies: (A−λI)kx=0, but (A−λI)k−1x̸=0.
Detailed Explanation
The mathematical definition of generalized eigenvectors indicates their rank, which describes how many times we have to apply the matrix operation
(A−λI) to the vector x before we reach the zero vector. In simpler terms, a generalized eigenvector is a vector that, when we apply the transformation represented by (A−λI) k times, results in zero. However, if we apply it one less time (k-1 times), we should still have a non-zero result, indicating that while it is not a traditional eigenvector, it still provides important structural information about the matrix and its eigenvalues.
Examples & Analogies
Think of this process like a lever that requires several pushes to reach the ground. If you push it once (k-1), it barely moves. If you push it twice (k), it drops straight down (the effect of the transformation equals zero). This lever represents the connection between traditional eigenvectors and generalized eigenvectors—each push corresponds to applying the transformation operation on the vector.
Jordan Canonical Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These vectors help form a Jordan canonical form, which generalizes the diagonal form for matrices that are not diagonalizable.
Detailed Explanation
The Jordan canonical form is a structured way to represent matrices that are not diagonalizable, giving us a clearer view of their properties. This form organizes the matrix in blocks that correspond to its eigenvalues and their associated generalized eigenvectors. It serves as a bridge between the diagonal representation (which involves full sets of independent eigenvectors) and matrices that may need additional structure due to repeated eigenvalues or lack of distinct eigenvectors. By using Jordan blocks, we can extract valuable information on how these matrices behave in different applications.
Examples & Analogies
Picture a team that needs to be organized into smaller groups for a project, but some members can work in multiple teams. Instead of forming completely separate teams (diagonal representation), you group them in a way that some groups share members, allowing collaboration while still representing everyone involved. This is akin to how Jordan canonical forms can help manage relationships within matrices that have the complexity of repeated elements.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Generalized eigenvectors arise in non-conservative systems or damped vibration problems, where the governing matrices are not symmetric and do not admit diagonalization.
Detailed Explanation
In civil engineering, especially in the analysis of structures subjected to complex loading conditions, generalized eigenvectors become crucial. For instance, in systems where energy is lost through damping (like a vibrating building during an earthquake), the matrices that model these systems often cannot be diagonalized using standard eigenvectors. Generalized eigenvectors provide alternative solutions to understand how such structures may behave over time, helping engineers predict potential failure modes and ensure stability.
Examples & Analogies
Consider a bridge that experiences vibrations during strong winds. If we simplify the structure using fixed points (normal eigenvectors), we overlook the nuances that wind brings to its performance. Instead, using generalized eigenvectors allows engineers to account for the effects of changing conditions—like winds that don’t always push uniformly—ensuring a more realistic assessment of the bridge's safety and structural integrity.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Generalized Eigenvectors: Extend the concept of eigenvectors for matrices with repeated eigenvalues.
-
Jordan Canonical Form: A format for matrices enabling the inclusion of generalized eigenvectors.
-
Rank: Number of matrix applications needed to achieve the zero vector with a generalized eigenvector.
-
Applications in Engineering: Importance in stability analysis and vibration damping in structures.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a vibration problem where stiffness and mass matrices are non-symmetric, generalized eigenvectors allow analysis of the system's dynamic behavior.
-
In structural stability, a bridge with repeated eigenvalues might require the Jordan form for effective analysis under load conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvectors are neat, when they’re unique,;
📖 Fascinating Stories
-
Imagine a builder named Jordan who struggled to group his beams for a project. He realized some beams could not stand alone and formed a group called the 'generalized beams', allowing him to design a stronger structure, which he called the Jordan form!
🧠 Other Memory Gems
-
G.E.C. - Generalized Eigenvectors Create stability in rotational dynamics.
🎯 Super Acronyms
GEN
- Generalized Eigenvectors Needed for complex systems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Generalized Eigenvector
Definition:
An eigenvector associated with a repeated eigenvalue that satisfies
(A−λI)^k x=0for a certain rank k. -
Term: Jordan Canonical Form
Definition:
A block diagonal form of a matrix that allows for the representation of generalized eigenvectors.
-
Term: Rank
Definition:
The number of times a matrix transformation must be applied before yielding the zero vector.
-
Term: Damped Vibration
Definition:
Oscillation of a structure that decreases in amplitude over time due to energy loss from friction or resistance.