Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Pressure Distribution in Fluids
Unlock Audio Lesson
Today we will first explore how pressure in a fluid at rest is distributed. Can anyone tell me how pressure changes when you go deeper into a fluid?
I think it increases with depth!
"Correct! We can express this mathematically as $P =
Hydrostatic Bench Experiment
Unlock Audio Lesson
Next, let’s discuss the hydrostatic bench experiment. What do you think its purpose is?
Is it to show how pressure is transmitted in fluids?
Yes! It demonstrates Pascal's law. Remember, 'Pascal = Pressure Everywhere'. Can someone explain how that works?
Pressure applied to any part of a confined fluid is transmitted uniformly throughout.
Exactly! This principle allows us to design hydraulic systems. How would you calculate the resulting force on a submerged surface?
By integrating the pressure distribution over the area!
Well done! Remember that to understand these applications, visualize the pressure diagram: a triangle forms as depth increases. Let's recap today's main concepts.
Forces on Submerged Surfaces
Unlock Audio Lesson
Now, let’s talk about forces acting on submerged surfaces. How do we determine the resultant force due to hydrostatic pressure?
We calculate the pressure at different depths and then find the average pressure over the area?
Right! The resultant force acts at a specific point we call the center of pressure. Do you remember how this is determined?
It’s typically one-third from the base of the submerged area!
Exactly! Now, let’s move to stability. What factors influence the stability of a floating body?
The positions of the center of buoyancy and center of gravity!
Great! If the center of buoyancy is directly below the center of gravity, the body is stable. Let’s summarize these points before we move on.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore key principles of hydrostatics, focusing on the characteristics and behavior of fluids at rest. Key topics include pressure variations with depth, applications of Pascal's law, and practical problem-solving techniques for calculating forces acting on submerged surfaces. We also discuss the stability of floating bodies based on the center of buoyancy and center of gravity.
Detailed
Detailed Summary of Basic Hydrostatic Concepts
Hydrostatics is the study of fluids at rest and the forces exerted by them. This section delves into essential concepts that form the foundation for understanding fluid behavior in various applications. The key points covered include:
- Pressure Distribution: In a static fluid, pressure increases linearly with depth according to the formula:
$$P =
ho g h$$
where $
ho$ represents fluid density, $g$ is the acceleration due to gravity, and $h$ is the depth.
- Hydrostatic Bench Experiment: A practical demonstration setup used to validate Pascal's law, which states that pressure applied to a confined fluid is transmitted undiminished in all directions.
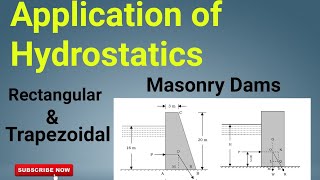
- Forces on Submerged Surfaces: The determination of net forces acting on submerged surfaces, important for calculating the design of structures like dams and gates. This includes understanding how to compute the resultant force from pressure distributions.
- Stability of Floating Bodies: The concepts of center of buoyancy and center of gravity are used to analyze the stability of floating bodies. Stability conditions are evaluated based on the relative positions of these centers.
These principles, along with practical problem-solving exercises, equip students with a comprehensive understanding of hydrostatic concepts necessary for advanced studies in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydrostatic Pressure Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know very basic things, when you consider z as a at the free surface level is zero. As z increases in the downwards the pressure will be P = ρgh.
Detailed Explanation
In hydrostatics, when we consider fluids at rest, we can establish that pressure increases with depth. Here, 'z' represents the depth below the free surface of the liquid. At the free surface, where z = 0, the pressure is atmospheric pressure. As we go deeper into the fluid, the pressure increases linearly according to the formula P = ρgh, where ρ is the fluid's density, g is the acceleration due to gravity, and h is the depth below the surface. This equation tells us that for every unit increase in depth, the pressure increases by a factor proportional to the density of the fluid and gravity's pull.
Examples & Analogies
Think of diving into a pool. When you first dive in, the pressure on your ears is minimal. However, as you swim deeper, the pressure increases significantly, which is similar to how hydrostatic pressure works; the deeper you go, the greater the pressure due to the water above you.
Buoyancy and Stability of Floating Bodies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Next one what we know is how a floating body’s stability is analyzed with respect to BM and BG, the distance between the buoyancy to metacenter points.
Detailed Explanation
In fluid mechanics, when an object is floating in a fluid, we analyze its stability using two points: the center of buoyancy (B) and the center of gravity (G). The center of buoyancy is the point where the buoyant force, which acts upwards to support the weight of the object, is applied. The metacenter (M) is a point where the buoyancy acts when the body is tilted. If the center of buoyancy is above the center of gravity, the object is stable. If it is below, the object will be unstable and may tip over. The distances between these points can tell us a lot about the stability of the object when it is floating.
Examples & Analogies
Imagine a boat on a lake. When the boat is upright and balanced (like the center of gravity is below the center of buoyancy), it floats steadily. If a person on one side of the boat moves too far, it tips and could capsize (representing an unstable condition), which can be visualized by thinking about how maintaining balance on a seesaw works.
Capillarity and Surface Tension
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similarly, we derived the capillarity height in terms of the diameter of the capillary tube. The formula is given by: h = (4σcosθ) / (ρg).
Detailed Explanation
Capillarity refers to the ability of a liquid to flow in narrow spaces without the assistance of external forces. This phenomenon is particularly noticeable in thin tubes, known as capillary tubes. The height to which the liquid rises in the tube can be calculated using the formula h = (4σcosθ) / (ρg), where σ is the surface tension of the liquid, θ is the contact angle, ρ is the liquid's density, and g is the acceleration due to gravity. This formula illustrates how surface tension and the diameter of the tube influence the height of the fluid within it.
Examples & Analogies
A practical example of capillary action can be seen when you place a straw in a glass of water; the water rises inside the straw. The narrower the straw, the higher the water will rise due to greater capillary action, which can be compared to how a sponge absorbs water.
Linear Pressure Distribution in Static Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When considering pressure at a point in the fluid, P = ρgh, can help us compute pressure distributions when the fluid is at rest.
Detailed Explanation
The equation P = ρgh is foundational for understanding how pressure works in static fluids. It states that the pressure at a specific depth (h) is directly proportional to the fluid's density (ρ) and the acceleration due to gravity (g). This relationship emphasizes that deeper points in a fluid experience greater pressure, which is essential for many applications in engineering and physics.
Examples & Analogies
Consider a large aquarium; the water pressure at the bottom of the aquarium is significantly higher than at the surface. If you were to take a measurement at various depths, you would find that the pressure increases consistently, illustrating this principle in action.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Distribution: Pressure in a static fluid increases linearly with depth, described by the equation P = ρgh.
-
Pascal's Law: Pressure applied at any point in a confined fluid is transmitted equally in all directions.
-
Resultant Force on Surfaces: Calculating the net force on submerged surfaces involves considerations of pressure distribution.
-
Stability of Floating Bodies: Stability is determined by the relative positions of the center of buoyancy and the center of gravity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of pressure distribution using a water tank scenario showing how pressure increases with depth.
-
Application of Pascal’s Law in hydraulic lift systems, demonstrating equal pressure transmission.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure builds down, like a crown, deeper you go, more force will flow.
📖 Fascinating Stories
-
Imagine a tall glass of water. The deeper you reach, the heavier it feels. That's how pressure works in fluids.
🧠 Other Memory Gems
-
Remember 'PDC' for Pressure, Depth, and Correspondence (Pascal's Law).
🎯 Super Acronyms
PDEP = Pascal’s law, Density, Elevation, Pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces exerted by them.
-
Term: Pressure
Definition:
The force applied perpendicular to the surface of an object per unit area.
-
Term: Center of Buoyancy
Definition:
The center of mass of the displaced fluid volume, critical for stability analysis.
-
Term: Pascal's Law
Definition:
A principle stating that a change in pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid.
-
Term: Static Fluid
Definition:
A fluid that is at rest.