Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydrostatic Pressure
Unlock Audio Lesson
Welcome everyone! Today, we're discussing hydrostatic pressure, which varies with depth in a fluid. Can anyone tell me what we mean by hydrostatic pressure?
Isn’t hydrostatic pressure the pressure exerted by a fluid at rest due to the weight of the fluid above it?
Exactly! Hydrostatic pressure increases with depth. The formula is P = ρgh, where ρ is the fluid density, g is the acceleration due to gravity, and h is the height from the free surface. Remember: 'P = ρgh' can help you recall how pressure increases in a stationary fluid.
Can you give an example?
Certainly! If you have water at a depth of 2 meters, the pressure at that depth would be approximately 19.62 kPa in SI units. Would you be able to calculate that if I gave you the density of water?
Yes, using the density of water which is around 1000 kg/m³!
Great! Let’s summarize this: hydrostatic pressure increases with depth due to the weight of the fluid above it.
Calculating Forces on Semi-Cylindrical Gate
Unlock Audio Lesson
Now that we understand hydrostatic pressure, let's apply it to a semi-cylindrical gate. Can anyone tell me what the concerns are when analyzing forces on such a gate?
We need to consider both horizontal and vertical forces acting on the gate?
Correct! The horizontal forces arise from the pressure distribution across the cylindrical surface. How would you find the resultant force acting horizontally?
We can calculate it by integrating the pressure over the area of the curved surface?
Absolutely! The formula would be Fh = ρg * A * cos(θ) where θ is the angle of the area considered. Now, let’s consider the vertical force.
Does that involve the weight of the liquid that the gate is displacing?
Yes! These vertical forces also help determine the equilibrium and moments about the hinge point of the gate.
To wrap it up, remember: calculate horizontal forces based on pressure distributions and account for vertical forces with liquid weight.
Equilibrium and Moments
Unlock Audio Lesson
Let’s now examine equilibrium conditions. Why is this vital when analyzing our semi-cylindrical gate?
The moments caused by forces must be balanced to keep the gate stable!
Exactly! The sum of moments around the hinge must equal zero. Can someone describe how we might express that mathematically?
If Fh creates a clockwise moment, we need to set it equal to the counter-clockwise moment caused by the vertical force, right?
Very well done! Thus, the general equation you might use is: Fh * distance from hinge - Fv * distance to CG = 0. Don’t forget to keep units consistent when you perform these calculations!
So we can solve for F or any unknown force?
Precisely! Always remember: equilibrium conditions are crucial in determining the forces acting on structures in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the teacher outlines the principles of hydrostatic pressure distributions on a semi-cylindrical gate. It covers the calculations necessary to find the forces acting on the gate, including horizontal and vertical components, and explores the concept of equilibrium in fluid statics.
Detailed
Detailed Summary
This section focuses on a specific problem related to fluid mechanics, particularly on the forces acting on a semi-cylindrical gate in a fluid. The teacher employs a systematic approach to solving GATE exam questions involving fluid statics. Key concepts include:
- Hydrostatic Pressure Distribution: The pressure in a fluid at rest varies with depth. This is illustrated by defining pressures at different points in a fluid column.
- Force Calculations: Students learn to calculate the net forces exerted by the fluid on the gate, comprising both horizontal and vertical components, to ensure equilibrium. The formula for the forces is derived from the pressure distribution diagrams.
- Equilibrium Conditions: The importance of equilibrium for static fluids is emphasized, where the sum of the moments around a pivot point must equal zero. The problem-solving technique involves summing forces and moments to find unknowns, such as the force acting on the gate.
This structured approach to analyzing semi-cylindrical gates not only prepares students for GATE exam questions but also deepens their understanding of fluid statics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Semi-Cylindrical Gate Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
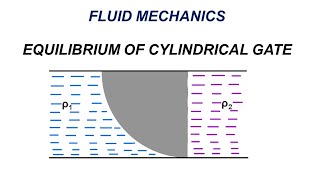
Now let us we another GATE questions we can solve it with as it is a diagrams given here. There is a semi circles cylindrical gate is there and force F is acting here and there is a hinge at this point. So we need to compute it if this is a free surface. This is the two meter depth of the water is there. What could be the force is required if the hinge at this point. This is what the questions.
Detailed Explanation
In this problem, we analyze a semi-cylindrical gate submerged in water. The gate is hinged at a point, which means it can rotate about that hinge. The depth of the water above the gate is 2 meters. Our goal is to determine the force needed to keep the gate in equilibrium. This involves understanding the forces acting on the gate due to the water pressure as well as the applied force F.
Examples & Analogies
Imagine a hinged trapdoor at the bottom of a swimming pool. If you wanted to keep the door closed while water presses against it, you'd need to apply a certain force to counteract the water pressure pushing on it. This scenario is similar to our semi-cylindrical gate problem.
Components of Forces Acting on the Gate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Flow classification: Fluid is homogeneous, Density is constant, Fluid is static. So there are the two force component will come it. One is a horizontal force and other is vertical force. And another F which is applied to here. So we will try to find out what could be this force component to compute, so that this will not rotate it. So we need to compute what is F is acting on this if there is a two force component, one is a horizontal force because the fluid at the rest.
Detailed Explanation
For the semi-cylindrical gate, we identify two key components of force acting on it: the horizontal force from the water pressure and the vertical force due to the weight of the water. These forces must be balanced for the gate to remain steady and in equilibrium. The horizontal force tends to push the gate outward, while the vertical force affects how deep the gate can be submerged without rotating.
Examples & Analogies
Think about how a large billboard stands against the wind. The wind exerts horizontal pressure on the billboard, trying to push it down, while the vertical force would be gravity pulling it down. Just as the billboard needs support to stay upright, the gate needs forces acting on it to maintain its position.
Calculating Horizontal Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now to compute horizontal forces, what is going to act it. So it is very easy that the places what will get it that what will be the force into vertical projections of the curved surface area. That is what we derived earlier. So we can compute it what will the force will act on this as the surface the pressure distributions where is like this, we can find out the pressures at the centroid locations. Horizontal force = \( \rho g h A \cos(\theta) \) (where A is the area of vertical projection).
Detailed Explanation
To calculate the horizontal force acting on the gate, we look at the pressure distribution over its surface. The pressure at any point increases with depth, and the total horizontal force can be found by integrating over the area of the gate that’s submerged. We use the equation presented where A represents the area projected vertically, and cosine of the angle adjusts for the orientation of the force acting on the area.
Examples & Analogies
Consider a kite in the wind. The wind applies force to the kite at different angles, much like water pressure on the gate. The more area the kite presents to the wind, the greater the force exerted on it. Similarly, the submerged area of the gate determines how much water pressure acts on it.
Calculating Vertical Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way if I need to compute how much vertical force is acting on this. So we can find out if this is my free surface. This is the area, the shaded part will give a vertical force component of F. The vertical force on portion BC = weight of liquid contained in the shaded area acting vertically upward = \( \rho g \cdot h \cdot A \).
Detailed Explanation
The vertical force acting on the gate is derived from the weight of the fluid above that gate. We calculate the vertical force by looking at the height of the water acting on the area of the gate that is submerged, expressed using the density of the water, gravity, and the area of the impacted surface.
Examples & Analogies
Think about how a boat floats on water. The weight of the water displaced by the boat pushes upward with a force equal to the weight of the water. In the case of our gate, the weight of the water above it pushes down, exerting a vertical force that we must consider.
Balance of Moments for Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
F for equilibrium taking moment about hinge 'O'. By taking moments about hinge, we establish that the sum of moments due to the forces acting must equal zero for equilibrium. The equation for moments gives us \( F \cdot r_1 = F_h \cdot r_2 \), balancing the horizontal and vertical moments.
Detailed Explanation
For the gate to be stable and not rotate, we need to ensure that the clockwise moments equal the counterclockwise moments about the hinge point. By calculating the distances from the hinge to where each force is applied and multiplying these distances by their respective forces, we can set up an equation to solve for the unknown force F. This step is crucial for finding the required force to maintain the gate’s balance.
Examples & Analogies
Imagine trying to balance a seesaw. If one side is heavier, you can adjust things (like moving a person closer to the hinge) to balance it out. In our problem, we’re doing something similar – balancing forces acting from different points to keep the gate from swinging open or closed.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Pressure exerted by a fluid at rest that varies with depth according to P = ρgh.
-
Natural Equilibrium: When the total forces and moments acting on a system are zero, allowing stability.
-
Moment Calculation: The process to determine rotational effects caused by forces acting at a distance from pivot points.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the pressure at a depth of 1m in water: P = 1000kg/m³ * 9.81m/s² * 1m = 9810 Pa approximately.
-
For a semi-cylindrical gate submerged in water, the resultant force can be derived from the pressure differentials acting on the gate.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure 'P' can be seen,
📖 Fascinating Stories
-
Imagine a gate at the edge of a beautiful lake. The deeper the water, the more pressure pushes against the gate. Remember, like a big hug from the water, the deeper it gets, the stronger the hug!
🧠 Other Memory Gems
-
Remember 'PEM' for pressure, equilibrium, and moments! It wraps the important concepts of static fluids.
🎯 Super Acronyms
FHE
- Forces
- Hydrostatics
- Equilibrium - the three essentials in fluid analysis!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at rest due to the weight of the fluid above a certain level.
-
Term: Equilibrium
Definition:
The state in which all forces acting upon an object are balanced, resulting in no net force or moment.
-
Term: Moment
Definition:
The measure of the tendency of a force to rotate an object about an axis, commonly referred to as torque.
-
Term: SemiCylindrical Gate
Definition:
A gate shaped like a half-cylinder used to control fluid flow.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid that opposes the weight of an immersed object.
-
Term: Specific Weight
Definition:
The weight per unit volume of a material; often used in fluid mechanics to describe the density of fluids.