Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Capillarity
Unlock Audio Lesson
Alright class, today we are focusing on capillarity. Can anyone tell me what happens when you place a straw in a glass of water? How does the water rise?
The water goes up the straw!
Exactly! This is a classic case of capillarity. The water rises due to the combination of cohesive forces among the water molecules and adhesive forces between the water and the straw.
But why does the water rise higher in a thinner straw?
Great question! The height to which the liquid rises in a capillary tube is influenced by the tube's diameter. A smaller diameter results in a higher rise, which can be quantified with the formula for capillary rise. Can someone summarize that formula?
It's h = (4 * σ * cos(θ)) / (ρ * g * d)!
Excellent! Remember, σ is surface tension, θ is the contact angle, and ρ is fluid density. Let's keep this in mind as we solve some practice problems.
In summary, capillarity is crucial for various processes like water transport in plants, and the height of rise in capillary tubes depends on surface tension and tube diameter.
Surface Tension Explored
Unlock Audio Lesson
Moving on to surface tension. Can anyone define it for me?
It's the measure of how difficult it is to stretch or break the surface of a liquid?
That's right! It's due to the cohesive forces among liquid molecules. Now, why do you think surface tension is important in everyday life?
It helps insects walk on water!
And it also causes water to form droplets!
Absolutely! Surface tension affects everything from how drops form to the behavior of liquids in different environments. The surface tension force can be calculated with T = ρgA. Can anyone remind me what each variable represents?
ρ is density, g is gravity, and A is the area!
Correct! Remember this formula as we apply it to real-world situations, such as understanding fluid behavior in engineering applications.
To conclude, surface tension plays an essential role in both nature and technology, influencing how liquids behave in various contexts.
Pressure in Fluids at Rest
Unlock Audio Lesson
Now let’s talk about pressure in static fluids. How does pressure change with depth in a liquid?
It increases with depth!
Exactly! In a static fluid, the pressure at a depth h can be expressed as P = ρgh. Can anyone tell me the significance of each variable?
ρ is the fluid density, g is acceleration due to gravity, and h is the depth.
Perfect! Let’s do a quick calculation. If we have water with a density of 1000 kg/m³ at a depth of 5 meters, what is the pressure at that depth?
P = 1000 * 9.81 * 5 = 49050 Pascals!
That's a solid calculation! Understanding pressure distribution in fluids is critical for engineering applications such as designing tanks or bridges.
To summarize, we’ve covered how pressure in static fluids increases with depth—key knowledge for handling liquid mechanics in various contexts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the basic concepts of capillarity and surface tension, including derived formulas and their applications. Key aspects such as the capillary height in relation to tube diameter and contact angle, as well as pressure distribution in fluids, are examined. Emphasis is placed on practical problem-solving and real-world applications.
Detailed
Capillarity and Surface Tension
Capillarity refers to the ability of a liquid to flow in narrow spaces without the assistance of external forces. This phenomenon is primarily due to the cohesive and adhesive forces acting between the liquid molecules and the surfaces with which they interact.
Surface tension is defined as the force per unit length acting along the surface of a liquid. This property allows liquids to resist external force and is crucial for phenomena like the formation of droplets and the ability of small insects to walk on water.
Key Concepts:
-
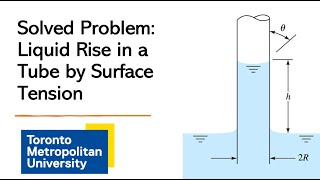
Capillary Rise: The height to which a liquid will rise in a capillary tube is proportional to the surface tension and inversely proportional to the diameter of the tube. The formula for the capillary height ( h) is derived as:
h = (4 cos θ)/(ρg), where θ is the contact angle, ρ is the fluid density, and g is the acceleration due to gravity. -
Surface Tension: The force of surface tension can be calculated with:
T = ρgA, where T is the surface tension force, ρ is the density of the liquid, g is gravity, and A is the area.
Application and Significance:
Understanding these concepts is essential for engineering applications involving fluid mechanics, including but not limited to, the design of hydraulic systems, the analysis of natural systems (like trees drawing water from roots), and in predicting the behavior of fluids in various environments.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Capillarity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Capillary height is given by the formula:
\[ h = \frac{4\sigma \cos(\phi)}{\rho g d} \]\n
where:
- \( h \) = capillary height
- \( \sigma \) = surface tension force
- \( \phi \) = angle of contact
- \( d \) = diameter
- \( \rho \) = density
- \( g \) = acceleration due to gravity.
Detailed Explanation
Capillarity is the ability of a liquid to flow in narrow spaces without the assistance of external forces. The height to which a liquid can rise in a capillary tube is determined by the balance between adhesive forces (the attraction between the liquid molecules and the tube wall) and cohesive forces (the attraction between liquid molecules themselves). The given formula quantifies this relationship, showing that capillary height depends on the surface tension of the liquid, the angle of contact with the tube, the fluid's density, gravity, and the diameter of the tube.
Examples & Analogies
Think of capillarity like using a straw to drink juice. When you suck on the straw, the juice moves up against gravity, much like water rises in a narrow tube due to capillary action. The narrower the straw (smaller diameter), the higher the juice can rise because of the stronger adhesive forces acting between the liquid and the straw's wall.
Surface Tension and Pressure Differential
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The surface tension force can be equated with pressure difference across a liquid surface:
\[ F_{S} = \sigma \, A \]\n
This relates to the net force acting on the liquid due to surface tension.
Detailed Explanation
Surface tension is the elastic tendency of a fluid surface that allows it to acquire the least surface area. The formula relates the force exerted by surface tension to the area of the liquid surface. When a liquid meets a gas (like air), the difference in pressure on either side of the liquid surface creates a net force. This net force can be influenced by the surface tension and acts to minimize the surface area.
Examples & Analogies
Consider a soap bubble. Its surface is under tension, which keeps it spherical because this shape has the least surface area. If you poke the bubble, you disrupt this surface tension and the bubble pops, demonstrating how surface tension works to maintain its shape against external forces.
Pressure Distribution in Static Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The pressure in a fluid at rest varies with depth:
\[ P = P_{0} + \rho g z \]\n
where:
- \( P \) = fluid pressure at depth \( z \)
- \( P_{0} \) = atmospheric pressure at the fluid surface
- \( \rho \) = density of the fluid
- \( g \) = acceleration due to gravity.
Detailed Explanation
In a static fluid, the pressure increases as you go deeper due to the weight of the fluid above. This relationship can be represented with the formula where pressure at any depth is the sum of atmospheric pressure and the weight of the fluid above that point. The deeper you go into the fluid, the greater the pressure due to the additional weight of the fluid above.
Examples & Analogies
Imagine you're at the beach and swimming. As you dive deeper underwater, you might feel the weight of the water pressing down on you—this is what is happening with pressure in a static fluid. The deeper you go, the more water (weight) is above you, increasing the pressure you feel.
Equilibrium in Floating Bodies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For floating bodies, the stability can be analyzed using the concepts of the center of buoyancy (B) and the center of gravity (G). The distance between B and G determines stability.
Detailed Explanation
A floating object is stable if the center of buoyancy (the centroid of the volume of displaced fluid) is vertically above the center of gravity (the point where the weight of the object is considered to act). If G is below B, the object will tend to return to an upright position when tilted. However, if G is above B, the object may capsize or tip over because the buoyant force won't be able to bring it back to its equilibrium state.
Examples & Analogies
Think of a seesaw. If a heavier person sits closer to the middle, the seesaw remains balanced and stable. However, if a lighter person sits far from the middle, the seesaw may tip over, similar to how a floating object is stable or unstable depending on the position of its buoyancy and gravity centers.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Capillary Rise: The height to which a liquid will rise in a capillary tube is proportional to the surface tension and inversely proportional to the diameter of the tube. The formula for the capillary height ( h) is derived as:
-
h = (4 cos θ)/(ρg), where θ is the contact angle, ρ is the fluid density, and g is the acceleration due to gravity.
-
Surface Tension: The force of surface tension can be calculated with:
-
T = ρgA, where T is the surface tension force, ρ is the density of the liquid, g is gravity, and A is the area.
-
Application and Significance:
-
Understanding these concepts is essential for engineering applications involving fluid mechanics, including but not limited to, the design of hydraulic systems, the analysis of natural systems (like trees drawing water from roots), and in predicting the behavior of fluids in various environments.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Drinking through a straw demonstrates capillary action as the pressure difference created allows the liquid to rise.
-
The formation of water droplets on a leaf is an example of surface tension in action.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a small straw, water can flow, to heights it can rise with surface tension's glow.
📖 Fascinating Stories
-
There once was a water droplet who wanted to jump high, so it found a small straw and gave a try. With surface tension tight, it rose up the way, showing capillarity saves the day!
🧠 Other Memory Gems
-
CAP: Cohesion, Adhesion, and Pressure help remember key concepts related to capillarity.
🎯 Super Acronyms
SPLASH
- Surface tension
- Pressure
- Liquid Adhesion
- Surface Heights.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Capillarity
Definition:
The ability of a liquid to flow in narrow spaces without external forces, often observed in thin tubes.
-
Term: Surface Tension
Definition:
The force per unit length acting along the surface of a liquid, which results from the cohesive forces between liquid molecules.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above it.
-
Term: Cohesive Forces
Definition:
Attraction between molecules of the same substance that holds them together.
-
Term: Adhesive Forces
Definition:
Attraction between molecules of different substances, such as liquid and surface.