Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydrostatic Pressure
Unlock Audio Lesson
Welcome class! Today, we’re going to understand hydrostatic pressure, which is crucial for our example problems in fluid statics. Can anyone tell me what hydrostatic pressure is?
Isn't it the pressure exerted by a fluid at rest?
Correct! Hydrostatic pressure increases with depth due to the weight of the fluid above. It can be calculated using the formula P = ρgh. Who can tell me what each symbol represents?
ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height of the fluid column.
Exactly! Remember this with the acronym 'DGH' – Density, Gravity, Height. Now, why is understanding this pressure important when we analyze structures like dams or tanks?
Because it helps predict how much force the fluid exerts on the walls!
Great connection! So in our upcoming problems, we'll see how we apply this understanding. Let's summarize: Hydrostatic pressure is calculated as P = ρgh, and understanding it helps us predict fluid behavior and its effects on structures.
Calculating Forces on Submerged Surfaces
Unlock Audio Lesson
Now, let’s move on to calculating forces on submerged surfaces. Can anyone tell me how we can determine the force acting on a vertical gate submerged in water?
We need to find the pressure distribution first, right?
Exactly! We calculate pressure at different depths and integrate the pressure over the area. Let's take a gate that's 1.5 meters tall and calculate the force. If the top of the gate is at the free surface, how would we find the average pressure?
We can take P_avg = ½ ρgh, since it's a triangular pressure distribution.
Correct again! For our example, we substitute ρ = 1000 kg/m³ and g = 9.81 m/s² to find the force. Can anyone calculate the force for me?
I get 11.036 kN!
Perfect! Keeping this pressure distribution in mind will help you with many problems. Remember to visualize these scenarios, as it strengthens your understanding.
Buoyancy and Stability of Floating Bodies
Unlock Audio Lesson
Let’s delve into buoyancy now. Who can explain what buoyancy is?
It’s the upward force that a fluid exerts on an object submerged in it!
Exactly! This force can be calculated using Archimedes’ principle. If a body is floating, how do we determine its stability?
By analyzing the positions of the center of buoyancy and center of gravity!
Right again! Remember the acronym 'BGC' which stands for Buoyancy, Gravity, and Center. If BG is less than BM, the body is stable. Let's visualize a floating object and analyze its forces to reinforce this concept.
This makes it clearer how stability works! I really see how important these concepts are when designing ships or boats.
Absolutely! To summarize: Buoyancy is an upward force calculated as the weight of the fluid displaced, and stability relies on the relative positions of the center of buoyancy and center of gravity.
Utilizing Manometers
Unlock Audio Lesson
Now, let’s discuss manometers and how we can use them to measure pressure differences. What is a manometer?
It's a device used to measure the pressure of a fluid by balancing the column of fluid against the pressure being measured.
Correct! For example, if we have a gas connected to an inclined manometer, how would we read the pressure?
We measure the height difference in the manometer fluid and use it to calculate the pressure!
Exactly! And we can apply the formula involving specific gravity and the angle of inclination. Who would like to calculate a manometer reading with me?
I can do it! Let’s say the deflection is at 100 mm with a specific gravity of 0.86. I'll use the formula from earlier.
Great calculation! So, summarize: Manometers measure pressure by observing fluid height, and we can use specific gravity and angles to determine the exact pressure.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on fluid statics applications by solving ten problems from GATE and Engineering Service exams. It introduces essential concepts such as hydrostatic pressure, buoyancy, and manometry, providing detailed problem-solving techniques.
Detailed
Fluid Statics Applications: Example Problems
In this section, we explore the applications of fluid statics through a variety of example problems, particularly drawn from GATE and Engineering Service exam formats. Key topics covered include hydrostatic pressure distribution, buoyancy forces, and liquid manometers. We start by revisiting fundamental equations crucial for problem-solving in fluid statics, such as those relating to pressure distribution and buoyancy.
Key concepts involve the utilization of pressure gauges, manometers, and experimental setups. The significance of understanding hydrostatic pressure is emphasized as it lays the foundation for solving real-world problems involving fluid mechanics.
As we progress, we solve detailed example problems, including:
1. Pressure Calculation: Calculation of forces acting on gates submerged in fluids based on hydrostatic principles.
2. Equations of Hydrostatic Forces: Deriving forces due to static fluids acting at various points on submerged surfaces.
3. Buoyancy: Understanding the stability of floating bodies through their center of buoyancy (BM) and center of gravity (BG).
4. Manometer Readings: Utilizing manometers to ascertain pressure differences in fluid systems.
5. Application of Fluid Statics Principles: Solving complex problems involving equilibrium and the behavior of submerged objects.
These examples reinforce the theoretical concepts discussed and provide a practical understanding of fluid statics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Statics Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome all of you to Fluid Mechanics course. Today we are going to solve the problems on fluid statics. Looking that today I will cover with a introductions to hydrostatic bench experiment.
Detailed Explanation
In this introduction, the speaker welcomes the students to the Fluid Mechanics course and outlines the focus of the day’s lecture: solving problems related to fluid statics. The mention of a 'hydrostatic bench experiment' indicates that there will be practical demonstrations or experiments related to fluid pressures and behaviors that will help solidify the theoretical concepts discussed.
Examples & Analogies
Think of this introduction like a teacher announcing a science experiment day in class. Just like how experiments allow students to see theories in action, the hydrostatic bench experiment will help students visualize and understand fluid statics through practical examples.
Hydrostatic Bench Experiment Setup
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us look at the hydrostatic bench experiment setup, which is there in IIT Guwahati. So this type of experimental setups which is called this hydrostatic bench experiment setup, you can see the pressure gauge, you can see this mercury manometers. These are U-tube manometers are there.
Detailed Explanation
This chunk describes the setup of the hydrostatic bench experiment that includes key components such as pressure gauges and mercury manometers. These instruments are essential for measuring pressure differences in fluids, and the setup allows students to visualize how fluid statics operates in various conditions.
Examples & Analogies
Imagine visiting a laboratory where you can see real gauges measuring air pressure in tires or measuring the level of liquid in a glass. This experiment works the same way but with fluid statics, allowing students to make real-time observations of how pressure behaves in different scenarios.
Key Concepts and Formulae in Fluid Statics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us I just write the formulaes, okay. And just to repeat the things what we learnt it in fluid basic properties and the fluid statics that the Newton's laws of viscosities we established the relationship between shear stress and the velocity gradient.
Detailed Explanation
Here, the speaker summarizes fundamental concepts and formulas important for understanding fluid statics. These include Newton's law of viscosity, which describes how shear stress is related to the velocity gradient in a fluid, a vital concept for analyzing fluid motion and stability.
Examples & Analogies
Consider how honey moves slowly compared to water due to its viscosity. Just like honey requires more force to shake, the relationship laid out by Newton's law helps us understand why different fluids behave in specific ways when they are in motion or at rest.
Calculating Pressure in Fluid Statics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know very basic things, when you consider z as a at the free surface level is zero. As z increases in the downwards the pressure will be P = ρgh.
Detailed Explanation
This chunk discusses how to calculate pressure in a static fluid. It introduces the basic equation P = ρgh, where P is the pressure at depth z, ρ is the fluid density, g is the acceleration due to gravity, and h is the height of the fluid column. As depth increases in a fluid, pressure rises proportionately due to the weight of the fluid above.
Examples & Analogies
Think of being underwater while swimming. The deeper you go, the more pressure you feel against your body. This equation helps us quantify that pressure increase, explaining why divers must be careful to manage decompression when they ascend back to the surface.
Problem-Solving in Fluid Statics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
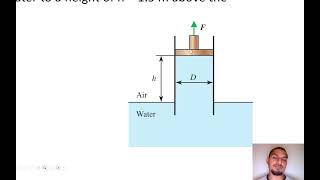
Let us start to solve the problems, these very easy problems that there is a square gate of dimensions of 1.5 meter into 1.5 meters...
Detailed Explanation
In this segment, the speaker initiates solving example problems, starting with a scenario involving a square gate in a water tank. The speaker outlines the necessary steps needed to compute forces acting on the gate using hydrostatic principles, emphasizing understanding pressure distribution and moments for equilibrium.
Examples & Analogies
Think of it like a door that opens inwards when a gust of wind pushes against it. By calculating how much force that wind exerts at different heights on the door, we can better understand whether the door will swing open or stay closed.
Continuing with Example Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us we another GATE questions we can solve it with as it is a diagrams given here. There is a semi circles cylindrical gate...
Detailed Explanation
This chunk discusses using a graphical representation to solve another example problem involving a semicircular gate. It emphasizes understanding the competing forces acting on the gate and how to balance them for equilibrium using moments, which is crucial in analyzing systems in static equilibrium.
Examples & Analogies
Think about how a boat floats on water. The weight of the boat pushes down while the water pushes up. In similar fashion, engineers often need to balance forces acting on structures to ensure they remain stable, just like ensuring a boat doesn’t tip over.
Manometer Problems and Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come it to a manometer problems. So there is a inclined manometer shown in the figure below...
Detailed Explanation
This section delves into solving problems associated with manometers, particularly inclined manometers. The application of pressure relationships to compute various pressures in liquid columns, based on incline angles and specific gravity, is discussed. This emphasizes the practical utility of manometers in measuring fluid pressure.
Examples & Analogies
You can think of a manometer as a tool similar to a thermometer but for pressure instead of temperature. Just as a thermometer helps you measure how hot or cold something is, a manometer lets you measure how much pressure a gas or liquid exerts, which can be crucial in many engineering applications.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Pressure due to the weight of fluid above; calculated using P = ρgh.
-
Buoyancy: The upward force on a submerged object; calculated based on the volume of fluid displaced.
-
Pressure Distribution: It's crucial for understanding how forces act on submerged surfaces.
-
Manometers: Instruments measuring pressure by observing the liquid height and using hydrostatic principles.
-
Specific Gravity: Important for determining fluid densities relative to water.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example problem on calculating the force acting on a submerged square gate.
-
A practical application of buoyancy in determining the stability of floating bodies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When liquids stay still, their pressure will build, Hydrostatic rules keep stability thrilled.
📖 Fascinating Stories
-
Imagine a floating castle on the lake, with buoyancy keeping it safe from a quake! The deeper it goes, the more pressure it shows, and that's how we find where stability flows.
🧠 Other Memory Gems
-
Remember 'BGC' - Buoyancy, Gravity, Center, for floating object stability in a water adventure.
🎯 Super Acronyms
Remember 'DGH' - Density, Gravity, Height for hydrostatic pressure calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic pressure
Definition:
The pressure exerted by a fluid at rest due to its weight.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid on an object submerged in it.
-
Term: Manometer
Definition:
A device used to measure fluid pressure using a column of liquid.
-
Term: Pressure distribution
Definition:
The variation of pressure across a given area of a submerged surface due to fluid weight.
-
Term: Specific gravity
Definition:
The ratio of the density of a fluid to the density of a reference substance, typically water.