Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Principles
Unlock Audio Lesson
Welcome everyone! Today, we're diving into fluid statics. Can anyone share what they understand by hydrostatics?
Isn't it about fluids at rest and how pressure behaves in them?
Exactly! Hydrostatics deals with fluids in equilibrium, mainly focusing on the pressure distribution within the fluid. Remember, the pressure increases with depth due to the weight of the fluid above it. We can summarize this with the formula P = ρgh, where P is the pressure, ρ is the fluid’s density, g is the acceleration due to gravity, and h is the height of the fluid column.
What about buoyancy? How does that relate to hydrostatics?
Great question! Buoyancy is the upward force exerted on a body submerged in a fluid, which relates to hydrostatic principles. It depends on the density of the liquid and the volume of the fluid displaced. We often use Archimedes’ principle here.
Can we derive the relationships in class?
Absolutely! Keep in mind that the key to understanding these concepts is applying the right formulas in problem-solving scenarios. Let's outline a few important formulas to remember!
In summary, hydrostatics involves understanding pressure with depth, buoyant forces, and how these principles apply to problems we will solve.
Examine Hydrostatic Pressure Distribution
Unlock Audio Lesson
Let’s delve deeper into pressure distribution in fluids at rest. Who can tell me how pressure changes as we move deeper into a fluid?
It increases linearly with depth?
Correct. The linear relationship means for every unit of depth, the pressure increases. Thus, we can use P = ρgh to find the pressure at any depth. Can anyone provide a practical example of this?
If we consider a water tank, we can calculate the pressure at the bottom using the height of the water column.
Well done! The atmospheric pressure also plays a role here. The total pressure exerted at any point is the sum of atmospheric pressure and the pressure due to the fluid column. How do we apply this to find forces on submerged surfaces?
We calculate the hydrostatic force acting on the surface by integrating the pressure over the area.
Right! Calculating these forces will help us solve various problems, especially in engineering applications.
To summarize, pressure distribution is fundamentally about depth, and calculating this effectively is crucial for fluid statics problems.
Applying the Concepts through Example Problems
Unlock Audio Lesson
Now let’s tackle some example problems together. I will describe a scenario involving a square gate in a reservoir. Can anyone summarize our approach?
We first need to draw the pressure distribution diagram, then calculate the resultant force exerted by the fluid.
Exactly. And where do we find that resultant force acts on the square gate?
It acts at a center of pressure typically located one-third from the base of the submerged surface.
Great! Let's use the example you brought up. The square gate we consider has dimensions of 1.5m x 1.5m and is fully submerged. The force on this gate can be calculated as follows...
Remember, when solving these problems, always set up your knowns and unknowns clearly. Let’s work through the steps together now.
In summary, breaking down the problem into steps – analyzing the pressure distribution and calculating the resultant forces – will streamline our problem-solving process.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into fluid statics problem-solving by analyzing example problems relevant to GATE and Engineering Services Exams. It covers essential concepts, formulas, and frameworks for tackling hydrostatics and pressure-related problems.
Detailed
Problem Solving in Fluid Mechanics
This section provides a comprehensive analysis of problem-solving techniques in fluid statics, with specific emphasis on applications in competitive exams like GATE (Graduate Aptitude Test in Engineering) and the Engineering Services Examination. The focus is on understanding the hydrostatic principles that govern fluid behavior in static conditions, exploring foundational concepts like pressure distributions, buoyancy, and forces acting on submerged surfaces. The section discusses crucial formulas, including the Newton's law of viscosity, capillary height determination, and pressure distribution formulas. Furthermore, it presents numerous example problems, elucidating how to apply theoretical knowledge to practical situations, thereby equipping students with the skills to navigate complex fluid mechanics scenarios effectively.
Youtube Videos
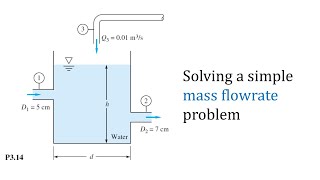
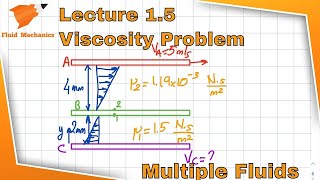
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Problem Solving in Fluid Statics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us start to solve the problems, these very easy problems that there is a square gate of a dimensions of 1.5 meter into 1.5 meters. One of the vertical sides of a fully filled water tank has one side on the free surface. It is hinged on the lower horizontal sides. Here it is a hinged it and is held in a positions by force applied on the vertical the central line at a depth of 0.75 meter below the free surface.
Detailed Explanation
In this section, we begin by examining a practical problem involving a square gate in a water tank. The key information here is the dimensions of the gate (1.5 m x 1.5 m) and its positioning—hinged at the bottom and one edge resting on the water's surface. Understanding how this system operates under static fluid conditions is critical. The force holding the gate in place is applied at a depth of 0.75 m below the surface of the water. This scenario illustrates how understanding hydrostatic pressure can help calculate forces acting on submerged or partially submerged surfaces.
Examples & Analogies
Imagine a large swimming pool with a floating cover. The cover rests on the water surface, but a wind gust pushes it down. The pressure of the water beneath the cover affects how much force the wind needs to exert to keep the cover afloat. In the same way, the hinge and force applied in our problem help keep the square gate in equilibrium against the pressure from the water.
Understanding Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One side of the square gate is fully in the water, and we need to calculate the total hydrostatic pressure acting on this gate. The pressure distribution varies with depth, being higher at greater depths due to the weight of the water above. The pressure at a certain depth h can be expressed as P = ρgh, where ρ is the density of the fluid and g is the acceleration due to gravity.
Detailed Explanation
Hydrostatic pressure is a fundamental concept in fluid statics, which indicates that the pressure increases with depth in a fluid due to the weight of the fluid above. Here, we can calculate the pressure using the formula P = ρgh, where 'ρ' represents the fluid's density, 'g' is the gravitational acceleration, and 'h' is the depth at which we are measuring the pressure. This formula provides the pressure at any depth in a static fluid, allowing us to understand how forces act on surfaces like the gate.
Examples & Analogies
Think of diving into a pool: the deeper you go, the more water pushes down on you. This pressure you feel isn't just because of the water's weight directly above you—it’s also the result of all the water in the pool pressing down from above. Similarly, each part of the square gate experiences different pressures proportional to its depth in the water.
Calculating the Resultant Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The total force exerted by the water on the gate can be calculated by integrating the pressure over the area of the gate. For a 1.5 m square gate, the average pressure at its center can be considered since pressure varies linearly. The horizontal force on the gate at any level can be calculated as F = (1/2 * height * width * average pressure).
Detailed Explanation
To calculate the total force acting on the square gate from the water, we consider the pressure distribution across its area. Since pressure increases linearly with depth, we average the pressure over the height of the gate. The formula F = (1/2 * height * width * average pressure) allows us to calculate the effective force without needing to consider every point along the height individually—this gives us a practical solution to find the resultant force efficiently.
Examples & Analogies
Imagine pressing a piece of paper against the surface of a pool. As you push deeper into the water, the pressure from the water increases. If you average the water pressure, you can estimate how hard you need to push to keep the paper submerged at a certain depth. Similarly, calculating the average pressure on the gate gives us an overall force value.
Finding the Point of Application of Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The center of pressure, where this resultant force acts, is located below the centroid of the gate. In a triangular distribution, which occurs in such cases, the center of pressure acts at 1/3 of the depth from the base. For this problem, we take moments about the hinge to establish equilibrium.
Detailed Explanation
In fluid statics, the location where the resultant hydrostatic force acts is known as the center of pressure. For submerged surfaces like our gate, this point is not at the geometric centroid but rather lower; specifically, for triangular distributions of pressure, it is found 1/3 the distance from the base to the centroid. We then consider this in our calculations by taking moments about the hinge to find the applied force required for equilibrium.
Examples & Analogies
Think about how a seesaw balances. If you have a heavier person further from the pivot point, they would need to push down harder to keep the seesaw level. Similarly, the center of pressure determines where to apply force relative to the hinge so that the gate remains stable in equilibrium.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Pressure exerted by a fluid at rest, varying with depth.
-
Pressure Distribution: The relationship between pressure and depth in a static fluid.
-
Buoyancy: The upward force on a submerged object, equal to the weight of displaced fluid.
-
Archimedes' Principle: Principle detailing the buoyant force acting on submerged bodies.
-
Resultant Force: Total force acting on a submerged surface, calculated using pressure distribution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Calculating the pressure at a depth of 5 meters in a lake.
-
Example 2: Determining the buoyant force acting on a submerged object with a volume of 0.1 m^3.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
At a depth so neat, pressure is a feat!
📖 Fascinating Stories
-
Imagine a tall glass of water; as you dive deeper, the weight of the water pushes down harder, creating more pressure!
🧠 Other Memory Gems
-
BAPH: Buoyancy, Archimedes, Pressure, Hydrostatics - remember the core concepts!
🎯 Super Acronyms
BP = ρgh (Buoyant Pressure is Density times Gravity times Height).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest, focusing on pressure distribution within these fluids.
-
Term: Pressure Distribution
Definition:
The variation of pressure in a fluid with depth, often represented as P = ρgh.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid on a submerged object, equal to the weight of the fluid displaced.
-
Term: Archimedes' Principle
Definition:
A principle stating that a body submerged in a fluid experiences an upward force equal to the weight of the fluid it displaces.
-
Term: Hydrostatic Force
Definition:
The force exerted by a fluid at rest on a surface in contact with it.