Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basics of the Hydrostatic Bench Experiment Setup
Unlock Audio Lesson
Today we’ll start with the basics of the hydrostatic bench experiment. Can anyone tell me what instruments we typically find in this setup?
I think we use pressure gauges and manometers?
Precisely! We use pressure gauges to measure pressure and manometers, especially U-tube manometers, to visualize pressure differences. Remember, when measuring pressure in fluids, the gauge readings can vary based on the fluid density and depth.
So does this mean that the shape of the container doesn’t affect the pressure at a given depth?
Correct! This is directly related to Pascal's law. It states that pressure within a fluid at rest is exerted equally in all directions. This is central to our understanding of fluid mechanics. Can anyone summarize this principle in terms of real-world applications?
I think it relates to how hydraulic systems work?
Exactly! Hydraulic lifts operate on this principle, where pressure is transmitted through a fluid to lift heavy objects.
In summary, we learned that the hydrostatic bench uses pressure gauges and manometers to illustrate Pascal's law, where pressure in a static fluid remains constant regardless of the container's shape.
Understanding Pressure and Its Distribution
Unlock Audio Lesson
Let’s discuss how pressure changes with depth in a fluid. What happens to pressure as we go deeper?
Pressure increases with depth, right?
Exactly! The formula we use for this is P = ρgh, where ρ is the density, g is the acceleration due to gravity, and h is the height of the fluid column above the point. Why do we care about this?
So we can calculate the forces acting on submerged surfaces?
Exactly! If we know a surface area and how deep in the fluid it is, we can calculate the total force acting on it due to the fluid pressure. Does everyone understand that concept?
Can you provide an example?
Certainly! If we have a gate submerged in water, we can calculate the force acting on it by finding the average pressure and multiplying it by the area. The total force can then be calculated using the hydrostatic pressure distribution.
To summarize, pressure in a fluid increases with depth, impacting the force on submerged structures, allowing us to apply this knowledge to practical examples in engineering applications.
Applications of Hydrostatic Principles
Unlock Audio Lesson
Now, let's tackle some problems we might face concerning hydrostatics principles. What type of problems do you think we could solve?
Calculating forces acting on gates or submerged objects!
Correct! To solve these problems, we first draw the pressure distribution and identify the forces acting. What should be our first step?
Determine the pressure at various depths?
Yes! And then calculate the resultant force by integrating the pressures over the area. Remember this crucial formula: F = P × Area, as we apply it to solve these problems.
Could you show us a specific example?
Absolutely! If we consider a square gate submerged in water, we can use the average pressure to get the force. Let’s practice by solving a similar problem together during our exercise session.
To summarize, we can analyze forces on submerged surfaces by first calculating pressure at various depths and then using these values to understand resultant forces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
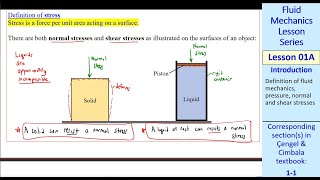
The hydrostatic bench experiment is a crucial setup in fluid mechanics, used to study fluid statics and pressure measurements. The section discusses different instruments used in the experiment, such as pressure gauges and manometers, as well as key principles like Pascal's law and pressure distribution in fluids.
Detailed
Introduction to Hydrostatic Bench Experiment
The hydrostatic bench experiment is designed to explore critical concepts in fluid statics. This section begins with an overview of the experimental setup at IIT Guwahati, highlighting key instruments such as pressure gauges, mercury manometers, and U-tube manometers used to measure fluid pressure.
It emphasizes Pascal's law, which states that pressure at a horizontal surface in a fluid at rest remains constant, regardless of the shape of the container. As fluids are filled to rest, the principles of hydrostatics govern the pressure distribution within them, leading to calculations based on dynamic viscosity and surface tension.
The section also covers formulas related to fluid mechanics, such as for capillary height and pressure distributions, establishing the foundational formulas needed to solve various problems in fluid mechanics. Finally, it transitions into practical applications by discussing methods to solve problems related to these concepts, such as calculating forces acting on submerged objects and pressure in manometric situations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Hydrostatic Bench Experiment
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us look at the hydrostatic bench experiment setup, which is there in IIT Guwahati. So this type of experimental setups which is called this hydrostatic bench experiment setup, you can see the pressure gauge, you can see the pressure gauge. You can see this mercury manometers. So these are mercury manometers are there. These are U-tube manometers are there.
Detailed Explanation
The hydrostatic bench experiment is a practical setup used to demonstrate principles of fluid statics. It includes instruments like pressure gauges and manometers, which are devices used to measure pressure in fluids. Mercury manometers and U-tube manometers are specifically mentioned. They work by balancing a column of liquid against the pressure being measured, allowing students to visually understand how fluid pressure varies with depth and fluid density.
Examples & Analogies
Imagine you're at a carnival where they have booths for games, and one game involves guessing the weight of a filled balloon hovering above. Similarly, the hydrostatic bench experiment allows us to 'guess' the pressure of a fluid using a manometer that 'balances' a column of liquid, just like guessing the balloon's weight based on its lift.
Pascal's Principle Demonstration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Not only that, there is the experiment setups to prove the Pascal's laws that the pressure in a horizontal surface remains the constant. That what you can see there is a different shape of the containers are there.
Detailed Explanation
Pascal's principle states that any change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid. In the hydrostatic bench experiment, different shapes of containers filled with fluid demonstrate that regardless of the shape, if the fluid is at rest, the pressure at a given depth is the same. This reinforces the idea that fluid pressure does not depend on the shape of the container but rather on the height of the fluid column above the measuring point.
Examples & Analogies
Think about a balloon filled with water. If you squeeze one side, the pressure is felt equally throughout the entire balloon, causing water to pop out of another part. This is a simple demonstration of Pascal's law in action, similar to what students observe in the hydrostatic bench experiment with different container shapes.
Importance of Measurements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You can have conduct different experiments using this pressure gauge as measurements, the manometer measurement, and U-tube manometers.
Detailed Explanation
The hydrostatic bench integrates various measurement tools like pressure gauges, manometers, and U-tube manometers for conducting experiments. These tools help quantitatively assess fluid behavior, offering a precise and visual way to study concepts of pressure, height, and fluid rest states.
Examples & Analogies
Think of it as a kitchen where you have different measuring cups and spoons. Just as you need precise measurements to bake a perfect cake, engineers need accurate measurements of fluid pressure and behavior to design safe and effective structures that interact with fluids.
Applications of Hydrostatic Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So when you fill up the fluid if it is at the rest you will have the same horizontal plane will be developed irrespective of whatever the shape of the containers.
Detailed Explanation
When fluids are at rest, the hydrostatic principles allow us to predict pressure variations accurately. Regardless of the container's shape, the pressure at any horizontal level remains constant, which simplifies calculations for engineers and scientists when working with fluid dynamics.
Examples & Analogies
Imagine two differently shaped glasses filled to the same height with water. Regardless of their shape, if you use a straw to check the water level inside both glasses, the water will rise to the same height in both straws. This exemplifies how pressure behaves in fluids at rest, reflecting the principles demonstrated in the hydrostatic bench experiments.
Future Concepts in Hydrostatics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what we discuss more detail while teaching the hydrostatics, basic hydrostatics concepts and we also derive the equations for that.
Detailed Explanation
The hydrostatic bench serves as a foundation for understanding further concepts in hydrostatics. Students learn to derive essential equations that govern fluid behavior, laying the groundwork for more advanced studies in fluid mechanics.
Examples & Analogies
Learning hydrostatics is like learning basic math before heading into algebra or calculus. The hydrostatic bench gives students the basic knowledge and equations that they will build on as they explore more complex topics in fluid dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fluid Statics: The study of fluids at rest and the forces and pressure associated with them.
-
Pressure Distribution: How pressure in a fluid changes with depth and is critical for calculating forces on submerged surfaces.
-
Pascal's Law: Key principle that governs the behavior of fluids in static conditions, stating that pressure changes apply universally through the fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating pressure at a depth of 2 meters in water and determining force on a submerged gate.
-
Application of Pascal's law in hydraulic systems to lift heavy loads using fluid pressure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids that rest, pressure is best, equal at depth, in every quest.
📖 Fascinating Stories
-
Imagine a water-filled balloon; as you go deeper, the pressure in the balloon increases evenly, just like the layers of a cake, consistent throughout.
🧠 Other Memory Gems
-
For pressure increase, remember: H = Height increases, P = Pressure increases, it's a simple impress!
🎯 Super Acronyms
P.A.P - Pressure Applies Perfectly (referring to Pascal’s law).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic bench experiment
Definition:
An experimental setup designed to study fluid statics and pressure measurements using various instruments.
-
Term: Pascal's law
Definition:
A principle stating that pressure applied to an enclosed fluid is transmitted undiminished in all directions.
-
Term: Pressure gauge
Definition:
A device used to measure the pressure of a fluid.
-
Term: Manometer
Definition:
A device used to measure the pressure of a fluid by balancing it against a column of liquid.
-
Term: Static fluid
Definition:
A fluid that is at rest and not in motion.