Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Surface Tension
Unlock Audio Lesson
Today we'll discuss surface tension. Who can tell me what they think it is?
Isn't it the force that makes water droplets round?
Exactly! Surface tension is that property of liquids that causes them to minimize surface area due to cohesive forces between molecules. We can think of it as an elastic 'skin' on the liquid surface.
How does it affect other properties of liquids?
Great question! It influences phenomena like capillarity, where liquid can rise in a narrow tube. Remember, 'CAP' for Capillarity And Pressure!
Can you explain how that works?
Sure! When liquid forms a meniscus in a tube, its height can be determined using the formula involving surface tension, tube diameter, and contact angle. Let's keep this idea in mind!
Mathematical Representation of Surface Tension
Unlock Audio Lesson
Now, let's look at the equations related to surface tension. Who can recall the formula for calculating capillary height?
Isn't it related to the diameter of the tube and the angle of contact?
Indeed! The capillary rise can be calculated using the formula: h = (2σ cos(θ))/(ρg r), where σ is surface tension, θ is the contact angle, ρ is the density, g is gravity, and r is the radius. Let's remember 'CAP = 2σ' for Capillarity And Pressure!
What about the forces acting due to surface tension?
Excellent. The net force due to surface tension can be found by equating it with pressure difference and area. Remember 'F = σL' where L is the length where the surface tension acts.
Applications of Surface Tension
Unlock Audio Lesson
Let's discuss applications. Can anyone give examples of surface tension in action?
Like water striders walking on water?
Yes! Those insects exploit surface tension to walk on water. Another example is the way liquids form droplets.
And it affects how we use liquids in engineering, right?
Exactly! In engineering, understanding how surface tension works helps in designs where fluid behavior is critical, such as in microfluidics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
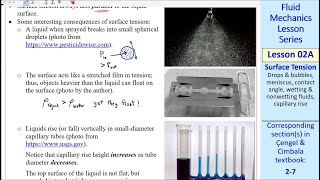
Surface tension is a fundamental property of fluids that arises due to cohesive forces at the liquid's surface. It is crucial in various applications, including capillarity and stability of floating bodies. Understanding surface tension and its implications is essential within fluid mechanics.
Detailed
Detailed Overview of Surface Tension
Surface tension is defined as the force exerted along the surface of a liquid that causes it to behave as an elastic sheet. This phenomenon is attributed to the cohesive forces between liquid molecules, which result in the liquid minimizing its surface area. The key equations governing surface tension, including those relating to capillarity and forces acting due to surface tension, are presented in this section. The effects of surface tension are significant in multiple applications such as calculating the capillary rise in narrow tubes and the stability of floating objects. Understanding these concepts helps in solving various engineering problems related to fluid statics and dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Surface Tension
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The surface tension force when we equate with a pressure difference and the area where it is acting it the force, both the side the force equating what you have done it the force the net force acting on this part is taking care of the force due to the surface tensions.
Detailed Explanation
Surface tension is a physical property of liquids that describes the elastic-like force existing at the surface of a liquid. It arises due to the cohesive forces between liquid molecules. When we consider forces acting on the surface of a liquid, such as in a capillary tube, the surface tension can be understood as a force acting along the surface of the liquid, effectively creating a difference in pressure. The forces on either side of a small segment of the liquid surface balance out, resulting in net forces that allow phenomena such as capillary action.
Examples & Analogies
A common example of surface tension can be seen when water forms droplets on a waxed car hood. The water clumps together due to surface tension, creating a spherical shape as the cohesive forces between the water molecules pull them inward.
Pressure Distribution in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know very basic things, when you consider z as a at the free surface level is zero. As z increases in the downwards the pressure will be P = ρgh. This indicates a linear pressure distribution when fluid is at rest.
Detailed Explanation
In fluids at rest, there is a direct relationship between the depth of the fluid and the pressure it exerts. This relationship is described by the equation P = ρgh, where P is the pressure, ρ is the fluid density, g is the acceleration due to gravity, and h is the height (or depth) of the fluid column. The deeper you go into the fluid, the greater the pressure due to the weight of the fluid above.
Examples & Analogies
Imagine a swimming pool. When you dive underwater, you feel the pressure increase as you go deeper. This is because the weight of the water above you is increasing, pushing down and exerting more pressure the further down you go.
Equilibrium Conditions in Buoyant Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Next, what we know is how a floating body’s stability is analyzed with respect to BM and BG the distance between buoyancy to metastatic points, the buoyancy to the center of gravity.
Detailed Explanation
In the analysis of floating bodies, understanding the relationship between the center of buoyancy (B) and the center of gravity (G) is crucial. The stability of a floating object depends on the distances between these points. The metacenter (M) is a point where the buoyancy force acts when the object is tilted. A stable floating object has its center of gravity below the metacenter, while an unstable one has it above. This principle is essential in naval architecture and engineering.
Examples & Analogies
Consider a toy boat floating on a lake. If the boat tilts slightly, the water under it tries to push it back upright. This ability to return to an upright position is due to the buoyancy being above the center of mass, providing stability like a tightrope walker balancing on a wire.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Surface Tension: The elastic force at the interface of a liquid.
-
Cohesive and Adhesive Forces: The fundamental forces responsible for surface tension.
-
Capillarity: The phenomenon of liquid rising or falling in a small tube due to surface tension.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water forming droplets on a waxed car surface due to surface tension.
-
A thin straw drawing liquid upwards due to capillarity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
There's a force so neat, on liquids it does greet; it's called surface tension, creating a fine sheet!
📖 Fascinating Stories
-
Imagine water forming cozy droplets; they love to stick together, thanks to their surface tension!
🧠 Other Memory Gems
-
Remember CAP for Capillarity And Pressure!
🎯 Super Acronyms
CATS - Cohesive Adhesive Tension Surface!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Surface Tension
Definition:
A force that causes the molecules at the surface of a liquid to be drawn inward, creating a 'skin' effect.
-
Term: Cohesive Forces
Definition:
Attractive forces between molecules of the same substance.
-
Term: Capillarity
Definition:
The ability of a liquid to flow in narrow spaces without the assistance of external forces.