Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today, we’ll explore the concept of hydrostatic pressure. Can anyone explain what hydrostatic pressure is?
Isn't hydrostatic pressure the pressure exerted by a fluid at rest?
Correct! Hydrostatic pressure increases with depth due to the weight of the fluid above. Who can tell me the formula for calculating hydrostatic pressure?
Is it P = ρgh?
Yes, that’s right! Here, ρ is the fluid density, g is the acceleration due to gravity, and h is the depth. Remember this formula, as it’s crucial for solving hydrostatic problems!
Pressure Distribution in Fluids
Unlock Audio Lesson
Now let’s discuss how pressure is distributed within a static fluid. How does pressure change with depth in a column of water?
I think it varies linearly with depth.
Exactly! The deeper you go, the greater the pressure. This linear relationship can be observed through pressure distribution diagrams.
Why is that important to understand?
It’s essential for predicting how fluids will behave in various engineering applications, like designing dams or storage tanks. Understanding the distribution allows engineers to calculate forces acting on surfaces.
Capillarity and Surface Tension
Unlock Audio Lesson
Let's shift our focus to capillary action. Can someone explain how it relates to pressure distribution?
I believe capillarity affects how high a liquid can rise in a narrow tube.
Exactly! This is a result of surface tension and adhesion to the tube’s walls. What formula can we use to calculate capillary height?
It's h = 4σcos(θ) / (ρg), right?
Yes! Well done. This relationship shows how capillary action can defy gravity, which is crucial in many biological and technological systems.
Problem Solving in Hydrostatics
Unlock Audio Lesson
Now let’s apply what we’ve learned to a specific problem. Imagine a square gate in a water tank. How would we compute the force acting on it due to hydrostatic pressure?
We can use the pressure distribution equation and integrate over the area!
Correct! You can calculate the force by finding the average pressure and multiplying it by the area. Would anyone like to attempt that calculation?
I can try! We need the depth and the area to calculate the pressure first.
Exactly! Let's work through it together, step by step.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the concept of pressure distribution in fluid statics, examines key formulas related to hydrostatic pressure, and addresses practical problem-solving techniques, including applications in engineering exams.
Detailed
In fluid mechanics, particularly in the study of fluid statics, pressure distribution is a fundamental concept that describes how pressure varies within a fluid at rest. When fluid is at equilibrium, the pressure at any point in the fluid depends on the depth of the fluid column above that point, thereby following a linear distribution characterized by the hydrostatic pressure equation. This section covers important formulas such as Newton's law of viscosity, capillary height, and formulations for static pressure. Additionally, practical applications, including example problems drawn from the GATE exam and Engineering Service Exam, are provided to enhance understanding and illustrate the problem-solving approach necessary for these topics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Pressure Distribution in Static Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When considering z as at the free surface level, it is zero. As z increases downwards, the pressure will be P = ρgh.
Detailed Explanation
In a static fluid, the pressure at any point increases with depth due to the weight of the fluid above it. The equation P = ρgh states that pressure (P) is equal to the product of the fluid's density (ρ), the acceleration due to gravity (g), and the depth (h) below the surface. The pressure is highest at the bottom of the fluid column and decreases to atmospheric pressure at the surface.
Examples & Analogies
Think of a stack of books. The pressure you feel at the bottom book is much greater than what you feel at the top book. This is similar to how pressure in a fluid increases with depth, as the weight of the fluid above you 'presses down' on you.
Linear Pressure Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This indicates a linear pressure distribution when fluid is at rest. If we consider atmospheric pressure equal to Patmospheric and at height h, the pressures can also be expressed simply as ρgh.
Detailed Explanation
The pressure distribution in a static fluid is linear because it varies directly with depth. At any point in the fluid, the pressure can be calculated using the formula P = Patmospheric + ρgh, where Patmospheric represents the pressure at the surface. This further emphasizes that as depth increases, so does the pressure in a linear manner.
Examples & Analogies
Imagine blowing up a balloon. At the top of the balloon, the air pressure is low, but as you push air into it, the pressure increases as you go lower into the balloon, much like how pressure behaves in a fluid.
Buoyant Force and Stability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We'll analyze the stability of a floating body concerning BM (metacentric height) and BG (distance from the center of buoyancy to the center of gravity).
Detailed Explanation
The stability of floating objects depends on their shape and weight distribution. The metacentric height (BM) is a measure of the stability of a floating body; if it is large, the body is stable. By analyzing the distances BG (from the center of gravity to the center of buoyancy) and comparing it to BM, we can predict whether the body will float upright or capsize.
Examples & Analogies
Consider a boat. When a person moves to one side of the boat, the center of gravity shifts, and the boat may lean. A boat designed to have a low center of gravity and higher metacentric height will be much more stable and less likely to tip over in the water.
Equating Forces in Hydrostatics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When considering the pressures and forces in hydrostatic conditions, the net force acting on a surface can be calculated as the weight of the fluid above it divided by the area.
Detailed Explanation
In hydrostatics, the force acting on a surface due to fluid pressure can be calculated by taking the weight of the fluid above the surface and dividing it by the area of that surface. This gives us the average pressure acting over that area, which is critical for designing structures like dams or underwater tunnels.
Examples & Analogies
Think of a large swimming pool. The water exerts pressure on the bottom, increasing as you go deeper. If you were to feel underwater, the pressure on your body would change based on how deep you were. Knowing this helps engineers design the flooring to withstand the water pressure effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Distribution: Refers to how pressure changes with depth in a fluid.
-
Hydrostatic Pressure Equation: P = ρgh, displaying the relationship of pressure to fluid density, gravity, and depth.
-
Capillarity: The phenomenon where liquids rise in narrow spaces against gravity due to surface tension.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating the pressure at a depth of 5 meters in a water column using P = ρgh.
-
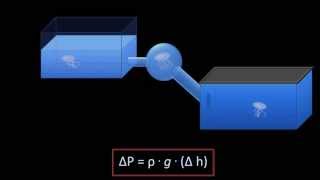
Demonstration of how a mercury manometer shows the pressure difference between two points in a fluid.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressures rise with depth, it's true, in liquids calm and clear as dew.
📖 Fascinating Stories
-
Imagine a deep well filled with water. The deeper you go, the heavier the water above presses down, increasing the pressure felt at the bottom - this is hydrostatic pressure.
🧠 Other Memory Gems
-
To remember how pressure rises: 'Depth is key, weight is best!'
🎯 Super Acronyms
H.P.
- Hydrostatic Pressure - Height and Pressure are linked profoundly.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest, increasing with the depth of the fluid.
-
Term: Pressure Distribution
Definition:
The variation of pressure within a fluid due to the weight of the fluid above and other forces.
-
Term: Capillarity
Definition:
The ability of a liquid to rise or fall in a narrow space due to surface tension.
-
Term: Surface Tension
Definition:
The cohesive force at the surface of a liquid that allows it to resist external force.