Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Newton's Law of Viscosity
Unlock Audio Lesson
Today, we will start with Newton's Law of Viscosity. Can anyone tell me how shear stress is related to the velocity gradient in fluids?
Isn't it that shear stress is directly proportional to the velocity gradient?
Exactly! We can express this relationship with the formula \( \tau = \mu \frac{du}{dy} \), where \( \mu \) is the dynamic viscosity. So remember, 'shear stress = viscosity times velocity gradient.' Can you think of a scenario where this applies?
Like flow in a pipe?
Good example! In pipe flow, we often examine how different fluids with varying viscosities behave. Remember, Viscosity can be thought of as the 'thickness' of a fluid.
So, if we had a thicker fluid, would the shear stress be higher?
Absolutely! A higher viscosity means more resistance to flow, resulting in greater shear stress. To recap, \( \tau = \mu \frac{du}{dy} \) is fundamental for understanding how fluids behave under shear. Great discussion today!
Capillarity and Surface Tension
Unlock Audio Lesson
Next, let’s dive into capillarity. Who can explain how the surface tension of water is related to its behavior in capillary tubes?
Isn’t it that water rises in the tube due to surface tension?
Exactly! The height of this rise can be calculated using the formula \( h = \frac{4\sigma \cos(\phi)}{\rho g d} \). What do each of these symbols represent?
Here, \( \sigma \) is the surface tension, \( \phi \) is the contact angle, \( \rho \) is the density, and \( d \) is the diameter of the tube.
Great job! Understanding this relationship helps in applications like designing inkjet printers or predicting behavior in biological systems. What’s the key takeaway?
That surface tension plays a critical role in fluid behavior!
Exactly! Remember, 'Surface tension = the pull that holds the liquid together.' Let's keep this in mind for our upcoming problems.
Hydrostatic Pressure Distribution
Unlock Audio Lesson
Now let’s talk about hydrostatic pressure distribution. How can the pressure at a certain depth be described?
I think it’s pressure increasing with depth. The formula is \( P = P_0 + \rho g h \)!
Well done! So pressure increases linearly; can you describe why this is significant?
It helps understand why deep-sea divers face pressure challenges!
Absolutely! The deeper underwater, the greater the pressure. For a metric, remember this: 'for every 10 meters, pressure increases by roughly one atmosphere.' Can you evaluate how this would apply to a scenario?
Like the conditions for underwater construction!
Exactly right! Understanding pressure distributions is critical in various engineering applications. Let’s be prepared to apply this knowledge!
Buoyancy and Stability of Floating Bodies
Unlock Audio Lesson
Lastly, let's discuss buoyancy. What determines whether a floating object is stable?
Is it the relationship between buoyancy and gravity?
Yes! The metacentric height helps us analyze stability. What does \( GM = BG - BM \) tell us?
It shows the relationship between the center of gravity and buoyancy. A higher metacentric height means more stability.
Correct! Remember 'Higher GM = Greater stability.' So, what applications can this principle support?
Boats and ships design!
Great insight! The understanding of buoyancy plays a key role in maritime engineering. Let's apply this to some upcoming problem sets!
Pressure Distribution and Forces on Surfaces
Unlock Audio Lesson
To tie everything together, we're exploring how pressure distributions affect forces acting on surfaces, like gates. How do we calculate that?
We integrate the pressure distribution over the area.
Exactly! For a gate submerged in fluid, net force \( F \) can be given by \( F = \int P dA \). Can you tell me about the pressure distribution shape for a submerged gate?
It’s triangular, right? The pressure increases with depth!
Spot on! Sharing this thinking with applications in dam design and flood management is vital. Let’s keep practicing these concepts in our problem sessions!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
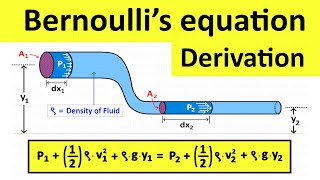
In this section, we delve into the fundamental formulas and derivations in fluid mechanics related to hydrostatics, highlighting the relationships governing hydrostatic pressure, buoyancy, and capillarity, along with problem-solving techniques used in examinations.
Detailed
Formulas and Derivations in Fluid Statics
In this section, we examine several critical formulas integral to the study of fluid statics:
- Newton's Law of Viscosity: This law establishes the relationship between shear stress and the velocity gradient, represented as
$$
\tau = \mu \frac{du}{dy}
$$
where \( \tau \) is the shear stress, \( \mu \) is the dynamic viscosity, and \( \frac{du}{dy} \) is the velocity gradient.
- Capillary Height Formula: The height of a liquid in a capillary tube can be expressed in terms of the tube's diameter, surface tension, and contact angle as follows:
$$
h = \frac{4\sigma \cos(\phi)}{\rho g d}
$$
where \( h \) is the capillary height, \( \sigma \) is the surface tension, \( \phi \) is the contact angle, \( \rho \) is the fluid density, and \( g \) is the acceleration due to gravity.
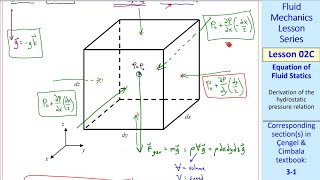
- Hydrostatic Pressure Distribution: The pressure at a certain depth \( z \) in a static fluid is described by:
$$
P = P_{0} + \rho g h
$$
which illustrates that pressure increases linearly with depth in a fluid at rest.
- Buoyancy: The stability of floating bodies can be analyzed using the relationship:
$$
\text{Metacentric Height} (GM) = BG - BM
$$
where \( G \) is the center of gravity, \( B \) is the center of buoyancy, and \( M \) is the metacenter. This relates to the stability of floating objects.
These formulas not only form the backbone for solving fluid statics problems but also directly support the application of principles in real-world scenarios such as designing dams, analyzing fluid flow in pipes, and assessing the behavior of floating structures. Understanding these concepts is crucial for students preparing for examinations such as the GATE and Engineering Services Exam.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Newton's laws of viscosities established the relationship between shear stress and the velocity gradient.
Newton's Law of Viscosity
\[ \tau = \mu \frac{du}{dy} \]
where:
- \( \tau \) = shear stress
- \( \mu \) = dynamic viscosity
- \( \frac{du}{dy} \) = velocity gradient
Detailed Explanation
Newton’s law of viscosity describes how fluid flows when a force is applied. Shear stress refers to the force per unit area that causes the fluid layers to slide past each other. The dynamic viscosity (μ) is a measure of a fluid's resistance to flow. When a fluid is in motion, the velocity of the fluid changes with distance from a surface. The velocity gradient (du/dy) shows how quickly velocity changes in relation to distance across the fluid. Therefore, the law essentially connects how hard you push (shear stress) and how quickly the fluid flows (velocity gradient).
Examples & Analogies
Imagine stirring honey with a spoon. The harder you stir (greater shear stress), the faster the honey moves (higher velocity gradient). If you stirred very gently (less shear stress), the honey flows slowly, demonstrating how viscosity affects flow.
Capillary Height Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We derived the capillarity height in terms of the diameter of the capillary tube:
Capillary Height
\[ h = \frac{4\sigma \cos(\theta)}{\rho g d} \]
where:
- \( h \) = capillary height
- \( \sigma \) = surface tension force
- \( \theta \) = angle of contact
- \( d \) = diameter of the capillary tube
Detailed Explanation
Capillary rise occurs when a liquid rises in a narrow tube due to the adhesive forces between the liquid and the tube material. The height to which the liquid rises (h) depends on several factors: surface tension (σ) which attracts the liquid upwards, the contact angle (θ) which describes how the liquid interacts with the tube walls, the density of the liquid (ρ), gravitational acceleration (g), and the tube's diameter (d). This equation allows us to predict how high the liquid will rise based on these parameters.
Examples & Analogies
Think of a straw in a drink. When you place the straw in the liquid, the liquid rises due to the interaction between the straw and the liquid. A thinner straw (smaller diameter) causes the liquid to rise higher compared to a wider straw, illustrating capillarity. The surface tension acts like tiny 'fingers' pulling the liquid upward.
Pressure Distribution in a Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When considering a fluid at rest, the pressure increases linearly with depth:
\[ P = P_0 + \rho g h \]
where:
- \( P \) = pressure at depth h
- \( P_0 \) = atmospheric pressure
- \( \rho \) = density
- \( g \) = acceleration due to gravity
- \( h \) = depth
Detailed Explanation
In a static fluid, the pressure at any point below the surface is determined by the weight of the fluid above it. This weight increases with depth, meaning that the pressure will also increase. The equation shows that the pressure at a given depth is the sum of the atmospheric pressure above the fluid and the hydrostatic pressure due to the fluid column above that depth. Essentially, the deeper you go, the more fluid weight is pushing down due to gravity, leading to higher pressure.
Examples & Analogies
Picture yourself at the beach. When you dive underwater, you feel the pressure on your ears increase as you go deeper. This sensation is due to the weight of the water above you pushing down more as you swim closer to the ocean floor.
Floating Body Stability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To analyze the stability of floating bodies, we look at the distance between the center of buoyancy (BM) and the center of gravity (BG):
- Stable Condition: If BM is above BG
- Unstable Condition: If BM is below BG
Detailed Explanation
The stability of a floating object, like a boat or a buoy, is determined by the positions of its center of buoyancy (BM) and center of gravity (BG). If the center of buoyancy is above the center of gravity, the object will be stable; it tends to return to an upright position if tilted. However, if the center of buoyancy is below the center of gravity, the object will be unstable; it will tip over easily. Therefore, understanding these positions helps engineers design boats and devices to ensure they remain upright in water.
Examples & Analogies
Consider a tall, thin lamp. If it's knocked, it will easily tip over because its center of gravity is higher than its support base, making it unstable. Now imagine a low, wide vase; it’s tougher to tip because the center of gravity is closer to ground level, increasing stability.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: The pressure exerted by a fluid due to its weight.
-
Buoyancy: The upward force exerted by a fluid on a submerged object.
-
Metacentric Height: A measure of the stability of a floating body.
-
Capillarity: The ability of a liquid to rise in narrow spaces due to surface tension.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A submerged gate experiences different forces at various depths, calculated using hydrostatic pressure formulas.
-
Water rises in a thin tube due to capillary action, demonstrating the effects of surface tension.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure dips as water's deep, buoyant force helps the ship to keep.
📖 Fascinating Stories
-
Imagine a tiny straw in a glass of water, as the water rises up the straw, it shows how surface tension works to lift the water higher.
🧠 Other Memory Gems
-
B.P.M. - Buoyancy, Pressure, Metacentric height - key concepts for fluid statics.
🎯 Super Acronyms
CAP - Capillary, Adhesion, Pressure - essential for understanding capillarity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
The force per unit area resulting from the application of a tangential force to a fluid.
-
Term: Dynamic Viscosity
Definition:
A measure of a fluid's resistance to shear or angular deformation.
-
Term: Capillary Action
Definition:
The ability of a liquid to flow in narrow spaces without the assistance of external forces.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above it.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid that opposes the weight of an object immersed in it.
-
Term: Metacentric Height
Definition:
The distance between the center of gravity and the metacenter of a floating body; a measure of its stability.