Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today, we'll start with understanding hydrostatic pressure. Can anyone tell me how pressure varies with depth in a fluid?
I think the pressure increases as we go deeper?
Correct! Pressure increases linearly with depth. This is known as hydrostatic pressure distribution. The equation is P = ρgh. Remember: ρ is density, g is acceleration due to gravity, and h is the depth.
So, if I have a fluid column, the pressure at any point is just the weight of the fluid above that point?
Exactly! Great understanding. We can visualize this with a simple diagram of a fluid column. It's crucial for calculating forces acting on submerged surfaces.
Calculating Forces on Gates
Unlock Audio Lesson
Let's move on to calculating forces on submerged gates. If we have a square gate submerged in water, how do we find the force acting on it?
By using hydrostatic pressure distribution to compute the pressure over the gate area?
Exactly, and then we use the average pressure times the area of the gate. Remember the formula: Net Force F = 1/2 × ρgh × A. Can anyone tell me what happens to the location of this force?
It acts at one-third the distance from the bottom of the gate!
Well done! This location is crucial for calculating moments about the hinge. Keep this in mind as we solve problems.
Using Moments to Find Equilibrium
Unlock Audio Lesson
Now that we understand how to find forces, let’s see how we can use moments for equilibrium. If we have a submerged object, how would we set up our equilibrium equation?
We should equal the moments about a point, like the hinge, to zero?
Exactly! The sum of moments around the hinge must equal zero for the object to remain stable. If F is the force acting on the surface and d is the distance from the hinge, our equation can be set up as: F × d - other forces × their distances = 0.
Can you give an example using this concept?
Sure! Imagine a triangular gate. By computing the forces acting on it and applying the moment equation, we can find the force needed to keep it at rest.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
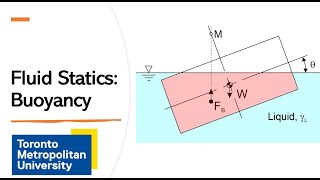
The section explains the principles of hinge moment calculation using examples involving hydrostatic forces on gates and submerged objects. It describes how to determine forces due to fluid pressure, the application of balance of moments, and the equilibrium conditions necessary for analysis.
Detailed
In this section, we explore the concepts of hinge moment calculations in fluid mechanics, emphasizing hydrostatics. The fundamental idea relates to understanding how forces from a static fluid act on objects such as gates and submerged surfaces. We begin by discussing how the pressure distribution acts linearly with depth and how hydrostatic forces can be calculated. Detailed explanations of various examples illustrate how to compute the resultant force acting on submerged objects and apply the principles of equilibrium to find hinge moments. Understanding how to balance these forces and moments is critical in designing fluid systems, ensuring stability and functionality in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hinge Moment Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
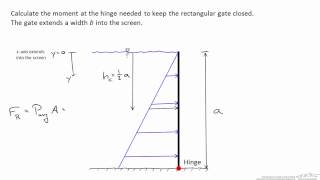
Now let us start to solve the problems, these very easy problems that there is a square gate of a dimensions of 1.5 meter into 1.5 meters. One of the vertical sides of a fully filled water tank has one side on the free surface. It is hinged on the lower horizontal sides. Here it is a hinged it and is held in a positions by force applied on the vertical the central line at a depth of 0.75 meter below the free surface.
Detailed Explanation
In this problem setup, we have a square gate with dimensions 1.5m x 1.5m. This gate is part of a vertical side of a water tank that is completely full. One side of the gate is at the water's free surface, and it is hinged at the bottom. A force is applied at the center of the gate, located 0.75 meters below the water surface. The goal is to compute the magnitude of this force, which is important in understanding how the gate interacts with the fluid pressure.
Examples & Analogies
Imagine a heavy door that is partially submerged in water. The pressure from the water pushes against the door, just like the pressure from the tank water acts on the gate. If you were to push the door to keep it closed, you would need to exert a force depending on how deep the water is, which parallels our calculation here.
Calculating the Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The magnitude of this force is? So this is 1.5 meters and 0.75 meters below means 0.75 meter from the bottom, from the hinge. This is what 0.75 meters, total is 1.5 meters. So what could be the magnitude of this force? The problem is that we need to know hydrostatic pressure distributions. Then we can compute the force due to the hydrostatic distribution.
Detailed Explanation
To find the force acting on the gate, we first need to understand hydrostatic pressure. Hydrostatic pressure increases linearly with depth due to the weight of the fluid above it. The pressure at any point in the fluid can be calculated using the formula P = ρgh, where ρ is the fluid's density, g is the acceleration due to gravity, and h is the depth from the fluid surface.
Examples & Analogies
Think of diving into a swimming pool. As you go deeper, you feel the weight of the water pressing down on you more strongly. This increasing pressure is similar to how hydrostatic pressure increases with depth in our water tank.
Center of Pressure and Moment Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once I know what is the force is acting because the fluid is at the rest and where it acts the force that the locations. If I know the force, the center of pressures or the force where is acting it, if I know that to the force magnitudes or the at the locations where the force acts then I can take a moment at the hinge locations to compute what will be the force component.
Detailed Explanation
The total hydrostatic force acting on the gate can be calculated as the average pressure multiplied by the area of the gate. The point where this force acts is known as the center of pressure. This point is not at the geometric center of the gate but depends on the pressure distribution. To maintain equilibrium, the moments about the hinge must balance, which is essential for calculating the applied force.
Examples & Analogies
Imagine pushing open a door. The point where you apply your push is critical for how easily the door swings. Similarly, in our problem, knowing where the hydrostatic force acts helps us balance the forces to find how much force is needed to keep the gate closed.
Moment Balance and Final Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Taking Moment about hinge (1.5/3) × F = F × 0.75. As you know in a triangular pressure distribution diagrams the resultant force acts at a one-third distance from the bottoms or two-third distance from the free surface.
Detailed Explanation
In this step, we calculate the moment about the hinge to find the required force F. The hydrostatic force acts at a distance of one-third the height of the gate from the bottom. We set up the moment balance: the moment due to the hydrostatic force equals the moment due to the applied force. Solving this gives us the magnitude of the applied force necessary for equilibrium.
Examples & Analogies
Think of using a seesaw. If you have a heavier partner on one side, you need to apply force on the other to keep it balanced. The moments on both sides must be equal for it to be level, just like how we balance the forces and moments on our hinged gate.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: The pressure due to the weight of a static fluid.
-
Resultant Force: The net force resulting from pressure on a submerged area.
-
Moment Calculation: Evaluating the moments about a hinge point for equilibrium.
-
Equilibrium Condition: The sum of forces and moments must balance to maintain stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: A square gate submerged in water has dimensions 1.5m x 1.5m. Calculate the hydrostatic force acting on it.
-
Example 2: An inclined manometer shows a deflection due to pressure in a gas pipeline. How to calculate the pressure at the pipeline end?
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids delve below, pressure starts to grow!
📖 Fascinating Stories
-
Imagine a boat immobile on water. The deeper we go, the heavier the water above, and that pressure increases.
🧠 Other Memory Gems
-
F = ρghA helps you remember how to find force based on liquid density, height, and area.
🎯 Super Acronyms
PHAP - Pressure, Height, Area, Force, all linked in hydrostatics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest, due to the weight of the fluid above it.
-
Term: Resultant Force
Definition:
The single force that represents the net effect of all the forces acting on a body.
-
Term: Equilibrium
Definition:
A state where the sum of forces and the sum of moments acting on a body are both zero.
-
Term: Hinge Moment
Definition:
The moment calculated about a hinge point due to forces acting on an object.