15.17. Bromwich Integral and Laplace Inversion Formula

Today, we're going to explore the Bromwich Integral, which is key to calculating the inverse Laplace transform.

What exactly does the Bromwich Integral do?

Great question! The Bromwich Integral allows us to retrieve a time-domain function from its Laplace transform by using a contour integral in the complex plane.

Could you explain what a contour integral is?

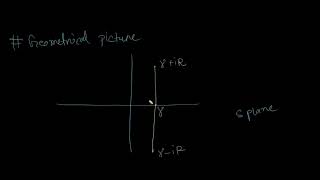
Certainly! A contour integral is an integral taken over a curve in the complex plane. In this case, we're integrating along a vertical line where the real part of 's' is greater than the real parts of any singularity of F(s).

So, why is it important to know where those singularities are?

That's critical because the contour must avoid the singularities; otherwise, our integral won't converge. Understanding where these points are helps us choose the right path for integration.

Can you give us a simplified expression of the Bromwich Integral?

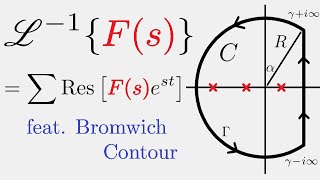
Of course! The integral is expressed as: $f(t) = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty} e^{st} F(s) ds$. Here, 't' is the variable in our time domain function and 's' is complex.

In summary, the Bromwich Integral is a fundamental tool for retrieving time-domain signals that have been transformed into the Laplace domain.

Now, let's talk about how the Bromwich Integral is applied in engineering, especially when dealing with vibrations.

How does this integral help in vibrations analysis?

When we have an equation in the Laplace domain, we can use the Bromwich Integral to transform it back to the time domain, allowing us to analyze how structures respond over time.

Can you give an example of this?

Certainly! If we have a transfer function related to a vibrating system, applying the Bromwich Integral helps us find the displacement or stress response over time due to dynamic loading.

What about stability analysis—is it similar?

Absolutely! The integral allows engineers to examine the stability of systems, indicating how they will respond to various initial conditions and forces.

So what's the key takeaway from today’s discussion?

The key takeaway is that the Bromwich Integral not only facilitates the mathematical transformation between domains but also has significant practical applications in engineering domains like vibrations and stability.