Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Fourier Cosine Transform
Unlock Audio Lesson
Today, we are going to tackle the Fourier Cosine Transform, abbreviated as FCT. It's a key concept, primarily used when analyzing functions in semi-infinite domains. Can anyone tell me what a semi-infinite domain is?
Isn't it a range that starts at a point and extends infinitely in one direction, like from 0 to infinity?
Exactly! Now, the formula for the FCT is \( F(ω) = \int_0^∞ f(x) \cos(ωx) \, dx \). This transformation helps us analyze the frequency components of a function using cosine functions. What do you think is the advantage of using cosine?
Cosines are useful for even functions, which simplifies our calculations?
Great observation! And how do we recover the original function from the transformed one?
We use the inverse Fourier Cosine Transform, which is \( f(x) = \frac{2}{π} \int_0^∞ F(ω) \cos(ωx) \, dω \).
Well done! Let's summarize today's key points. We learned the formula for FCT and its importance in solving problems in civil engineering involving semi-infinite domains.
Applications of the FCT
Unlock Audio Lesson
Now that we know what the FCT is, let's discuss its applications. Can someone think of a scenario in engineering where we might use the Fourier Cosine Transform?
I think it could be used in analyzing heat conduction in materials that only extend in one direction, right?
Absolutely! The FCT is particularly effective in heat conduction problems where we analyze how heat flows through materials. Can anyone relate this to a real-world example?
Maybe in the design of structures where we want to assess thermal effects on beams?
Yes, you've got it! By employing the FCT, engineers can predict how structures respond to thermal loads, which is crucial in ensuring safety and integrity. Let’s recap: we've identified important applications of the FCT in engineering contexts.
Understanding Cosine Properties
Unlock Audio Lesson
Let's delve deeper into the properties of the cosine function. How does the even property of cosine contribute to our analysis in the FCT?
Since cosine is an even function, it helps in simplifying the calculations when we only consider inputs from 0 to infinity.
Correct! The even nature allows us to focus on one side of the graph, and that’s particularly useful when solving differential equations. Can someone articulate why knowing these properties is beneficial?
It allows us to use symmetric properties of cosine to handle problems in a more efficient manner!
Right! Understanding the underlying principles boosts our problem-solving capabilities. To conclude, recall how the even character of cosine facilitates transformations and analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Fourier Cosine Transform (FCT) allows the transformation of a function into the frequency domain using cosine functions. This method is beneficial for solving partial differential equations (PDEs) in semi-infinite domains, providing both the transform and its inverse.
Detailed
Detailed Summary
The Fourier Cosine Transform (FCT) is an important mathematical tool used to convert a function defined over a semi-infinite domain (from 0 to ∞) into a frequency domain representation. The transform is given by:
\[ F(ω) = \int_0^∞ f(x) \cos(ωx) \, dx \]
where \( f(x) \) is the function being transformed and \( ω \) is the frequency variable. The inverse of this transformation, which allows you to retrieve the original function from its transformed version, is expressed as:
\[ f(x) = \frac{2}{π} \int_0^∞ F(ω) \cos(ωx) \, dω \]
This function is particularly useful for solving partial differential equations (PDEs) arising in semi-infinite domains, such as heat conduction or wave equations in civil engineering applications. The FCT's reliance on cosine functions caters to even functions, enabling the analysis to focus on symmetrical behaviors across the defined domain.
Youtube Videos
![Fourier cosine transform of e^(-ax)। Hence Evaluate integration from 0 to infinity [cossx/(x^2+a^2)]](https://img.youtube.com/vi/RJKhu_CoDcc/mqdefault.jpg)
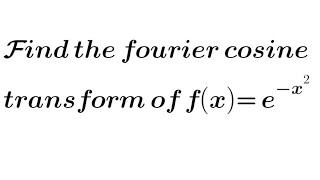
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Cosine Transform (FCT) Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Z ∞
F (ω)= f(x)cos(ωx)dx
c
0
Detailed Explanation
The Fourier Cosine Transform (FCT) is a technique used to transform a function from its time domain into a frequency domain. This transformation is represented mathematically by the integral of the product of the function f(x) and the cosine function cos(ωx), integrated from 0 to infinity. The variable ω represents the frequency, and F(ω) is the transformed function in the frequency domain. This transform focuses specifically on the cosine component of the function's Fourier representation, which is useful when dealing with even functions or specific boundary conditions.
Examples & Analogies
Imagine you're listening to music. Each note you hear can be thought of as a different frequency. The Fourier Cosine Transform is like isolating the specific notes in a song to see how prominently they feature in your listening experience. Just as you might focus on one melody out of many playing simultaneously, the FCT helps isolate specific behaviors of functions over time.
Inverse Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inverse:
2 Z ∞
f(x)= F (ω)cos(ωx)dω
π c
0
Detailed Explanation
The inverse of the Fourier Cosine Transform allows us to recover the original function, f(x), from its transformed frequency representation, F(ω). This involves integrating the product of F(ω) and the cosine function, cos(ωx), from 0 to infinity, scaling by a factor of 2/π. This process effectively reverses the transformation, enabling us to reconstruct the original function in the time domain, demonstrating the fidelity and utility of the Fourier transform methods in signal processing and analysis.
Examples & Analogies
Think of this process like baking a cake. When you bake a cake (the transform), you've created something new that might not look like the individual ingredients (the original time domain function) anymore. However, if you know the recipe (the inverse process) well enough, you can recreate the original ingredients (recover the function) just by looking at the cake. The inverse Fourier Cosine Transform acts as that recipe, helping you turn back to the original function from its frequency representation.
Applications of Fourier Cosine Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These transforms are particularly useful for solving partial differential equations (PDEs) in semi-infinite domains.
Detailed Explanation
Fourier Cosine Transforms are especially valuable in solving partial differential equations (PDEs) that arise in semi-infinite domains, meaning that they are defined for a range that extends infinitely in one direction. This is common in many physical problems related to heat conduction, wave motion, and vibrations where the medium extends indefinitely. The ability to transform these equations helps reduce them to a more manageable algebraic form, making it easier to find solutions that describe phenomena in fields such as civil engineering and physics.
Examples & Analogies
Consider modeling the temperature changes in a long, thin rod that is heated at one end. Because the rod extends infinitely in one direction, the Fourier Cosine Transform allows engineers to predict how heat travels through the rod. Think of it as dropping a pebble in a calm pond—the ripples (heat distribution) move outward infinitely. The FCT helps us understand these ripples more clearly, focusing specifically on how they behave in effect of the initial heating.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Cosine Transform: A tool for transforming functions in semi-infinite domains to the frequency domain.
-
Inverse Fourier Cosine Transform: The process of retrieving the original function from its cosine-transformed form.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using FCT to analyze how a beam's temperature will be distributed after a sudden heat source is applied.
-
Transforming a function representing the displacement of a vibrating system into the frequency domain for easier analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the heat and frequency rate, use FCT – don't wait, it simplifies the state.
📖 Fascinating Stories
-
Imagine a beam in the sun; its temperature rises, fun! FCT shows how heat will run, from hot to cold, it’s all done.
🧠 Other Memory Gems
-
FCT: 'Functions Come Together' in frequency analysis.
🎯 Super Acronyms
FCT
- Fourier Cosine Transform - remember it transforms functions!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform
Definition:
A mathematical transformation that converts a function defined on a semi-infinite domain into frequency space, utilizing cosine functions.
-
Term: Semiinfinite domain
Definition:
A range or interval that extends infinitely in one direction, typically from zero to infinity.