Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Laplace Transform for Discontinuous Functions
Unlock Audio Lesson
Today, we're going to discuss how Laplace transforms can simplify our work with piecewise and discontinuous functions, especially in civil engineering applications.
What are piecewise functions? Can you give us an example?
Great question! A piecewise function is one that is defined by different expressions or formulas in different parts of its domain. For instance, a function that describes a load on a beam might have one equation when a load is applied and another when it's removed. This is very common in engineering models.
And what about discontinuous functions? How do they fit into this?
Discontinuous functions have jumps or breaks in their graphs. The Laplace transform can effectively handle these types of functions because it allows us to convert them into an algebraic form, making them easier to analyze.
So, does that mean we can apply this in real-world engineering problems?
Exactly! Using the Laplace transform, we can analyze step loads, switching operations, and many other scenarios that are prevalent in civil engineering. Let's delve into the Unit Step Function next!
Unit Step Function
Unlock Audio Lesson
One critical function we use is the unit step function, defined as \( u(t-a) \). It essentially switches between 0 and 1 at a specific point, which is very helpful in modeling functions that start at a certain time.
How does that look mathematically?
"For \( t < a \), it's 0; for \( t \geq a \), it's 1. Thus, we can represent this mathematically as:
Transform of Shifted Functions
Unlock Audio Lesson
Now, let's look at shifted functions, which are crucial when we analyze responses that start after a delay.
What does that mean specifically?
A shifted function could be a situation where a force is applied after a certain time. The notation \( f(t-a)u(t-a) \) indicates that the function f start acting only after time a.
How do we transform that?
For such functions, the Laplace transform is given by \( L\{f(t-a)u(t-a)\} = e^{-as}F(s) \). This allows us to capture delayed responses efficiently!
That sounds very useful for real-life engineering problems!
Absolutely! This technique is essential for accurately modeling load systems and analyzing structural behaviors over time.
Review & Practical Application
Unlock Audio Lesson
Let's recap what we've learned about the Laplace transform for piecewise and discontinuous functions.
We talked about the importance of the unit step function!
And how shifted functions can represent delayed responses.
Exactly! Both concepts are crucial for analyzing civil engineering systems under various loading conditions. Does anyone want to try an example problem using these concepts?
Yes, let's try one together!
Great! Suppose we have a function representing a load applied at time a, how would we represent that?
We would use \( f(t-a)u(t-a) \) to denote that!
Correct! And what would the Laplace transform look like?
It would be \( e^{-as}F(s) \).
Excellent job, everyone! Remember, the key takeaway is the utility of the Laplace transform in simplifying complex, real-world problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses how Laplace transforms are used to effectively handle piecewise and discontinuous functions, particularly with the help of unit step functions. These techniques are essential for modeling real-world scenarios in civil engineering such as step loads and load removals.
Detailed
Detailed Summary
In many civil engineering applications, such as step loads or switching operations, functions can be defined in a piecewise manner or exhibit discontinuities. Traditional methods for analyzing these functions can be cumbersome, but using the Laplace transform provides a streamlined approach. This section highlights the utility of the unit step function (also known as the Heaviside function) as a tool for managing such complex functions effectively.
Key Points:
- Unit Step Function: Defined as \( u(t-a) \) where:
- \( u(t-a) = 0 \) for \( t < a \)
-
\( u(t-a) = 1 \) for \( t \geq a \)
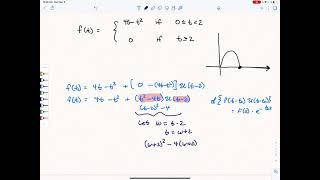
The Laplace transform of this function is \( L\{u(t-a)\} = e^{-as}/s \), which plays a pivotal role in transforming piecewise functions. - Transform of Shifted Functions: A piecewise function can often be expressed as a shifted function multiplied by the unit step function. If \( f(t) \) is defined for \( t \, \geq 0 \), the transform of a shifted function \( f(t-a)u(t-a) \) is given by \( L\{f(t-a)u(t-a)\} = e^{-as}F(s) \). This concept is crucial for modeling delayed responses in structural and load systems.
This section thus facilitates understanding how to leverage Laplace transforms in practical civil engineering scenarios, highlighting their power in simplifying the analysis of complex systems.
Youtube Videos
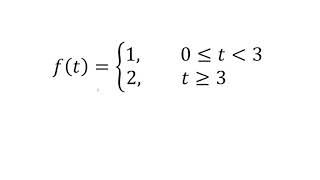
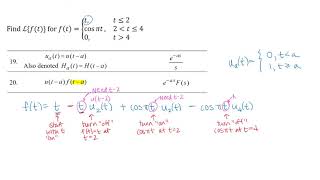
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Piecewise and Discontinuous Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering applications such as step loads, switching operations, and load removal, functions are often defined piecewise or are discontinuous. The Laplace transform can handle these efficiently using Heaviside (unit step) functions.
Detailed Explanation
In civil engineering, it’s common to encounter situations where loads (forces or weights) act on structures in a non-continuous manner. This means that instead of a single, smooth load applied over time, the load might change suddenly, like a switch turning on or off—this is termed a piecewise function. The Laplace transform is powerful because it can simplify the analysis of such functions. Specifically, it makes use of the Heaviside (unit step) function, which is a mathematical tool that helps model these abrupt changes in loads. The Heaviside function is defined to take the value of 0 before a certain time and 1 after that time, allowing engineers to mathematically describe events that occur at specific moments.
Examples & Analogies
Imagine a traffic light at an intersection. When the light turns green, cars start moving (load is applied), and when it turns red, they stop (load is removed). The abrupt switch from red to green can be viewed as a discontinuous function, like a step function. Just as engineers use the Laplace transform to analyze these sudden changes, traffic engineers might analyze the flow of cars at intersections based on these changes in signal states.
Unit Step Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Defined as:
$$
u(t-a) = \begin{cases} 0 & \text{if } t<a \\ 1 & \text{if } t\geq a \end{cases}$$
The Laplace Transform:
$$ L\{u(t-a)\} = \frac{e^{-as}}{s} $$
Detailed Explanation
The unit step function, denoted as u(t-a), is key in analyzing piecewise continuous functions. It is defined such that it is zero for times t less than a and one for times t equal to or greater than a. In the context of the Laplace transform, the equation $$ L\{u(t-a)\} = \frac{e^{-as}}{s} $$ shows how the Laplace transform changes the unit step function into a function of s. This transformation essentially incorporates the 'step' caused by the function into the Laplace domain, aiding engineers in understanding how systems behave when subjected to loads that start at a specific instant.
Examples & Analogies
Think of a birthday party where guests start to arrive at a specific time. Before that time, the number of guests is zero (the function is zero), and starting from that time, guests actively come in (the function becomes one). The unit step helps to mathematically clarify when the party starts—similar to how forces are applied to structures!
Transform of Shifted Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let f(t) be a function defined for t≥0, and consider f(t-a)u(t-a), a shifted function starting at t=a. Then,
$$ L\{f(t-a)u(t-a)\} = e^{-as}F(s) $$
This is essential for modeling delayed responses in structures and loading systems.
Detailed Explanation
This chunk focuses on functions that start acting at a delayed time, which is common in engineering problems where we only see effects after a certain time period (like structural responses after a load is applied). The expression $$ L\{f(t-a)u(t-a)\} = e^{-as}F(s) $$ indicates that when you shift a function f(t) to start at t=a instead of t=0 and multiply it by the unit step function, the Laplace transform can effectively capture this delay. The factor e^{-as} modifies the transform of the original function F(s) to account for the time shift, allowing engineers to predict how systems react to delayed forces.
Examples & Analogies
Imagine a runner in a race who starts running after a countdown, say, 5 seconds. Until the countdown is over, there is no movement (function is zero), but after that, the runner begins to run. Using the Laplace transform allows us to analyze not only when the running begins but also how fast the runner gains speed—capturing delays like this helps in designing better race tracks or physical systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Laplace Transform: A method for transforming a time-domain function into an algebraic representation for easier analysis.
-
Heaviside Function (Unit Step Function): A function that represents the turning on and off of systems at specific times.
-
Shifted Functions: Functions that are modified to start at a delayed point, allowing for the modeling of real-world scenarios academically.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A function that models a load applied at t = a can be represented as f(t-a)u(t-a), capturing the instantaneous effect at that moment.
-
Various civil engineering structures, such as bridges or beams, may experience step loads or immediate shifts in force that can be analyzed using these principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When loads shift and pause, use u(t-a), it gives a cause.
📖 Fascinating Stories
-
Imagine a building; at time a, workers start applying a load, described by f(t-a)u(t-a) to capture what happens from that point on.
🧠 Other Memory Gems
-
Remember 'SUDD' for piecewise - Step function, Unit step, Discontinuity, Derivation of Laplace.
🎯 Super Acronyms
U-SPL (Unit Step Piecewise Laplace) reminds us of the essential tie between these concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Piecewise Function
Definition:
A function defined by different expressions or formulas in different parts of its domain.
-
Term: Discontinuous Function
Definition:
A function exhibiting jumps or breaks in its graph.
-
Term: Unit Step Function (Heaviside Function)
Definition:
A function that is 0 before a certain point and 1 afterward, used extensively in engineering to represent sudden changes.
-
Term: Shifted Function
Definition:
A function that begins at a point other than zero, often represented using the unit step function.