Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Unit Step Function
Unlock Audio Lesson
Today, we are going to explore the Unit Step Function, u(t−a). It's a crucial tool when dealing with pieces in time, especially in engineering problems.
Can you explain what u(t−a) represents?
Absolutely! The Unit Step Function is defined such that it equals 0 for times before a specified point a and 1 for times equal to or greater than a. Imagine it as a switch that turns on at time a.
So, it models sudden changes in force, right?
Exactly! It’s vital for understanding how systems respond to sudden inputs. You can think of it as how a light turns on at a specific moment.
What happens if we need to represent a function that's shifted in time?
Good question! If you have a function defined as f(t) that starts at t=a, you can use u(t−a) as a multiplier to represent it correctly.
Could you recap the definition?
Of course! The definition of the Unit Step Function is crucial: it transitions from 0 to 1 at time a, representing a sudden action in engineering applications.
Laplace Transform of the Unit Step Function
Unlock Audio Lesson
Now, let’s talk about how we transform the Unit Step Function using the Laplace transform. The formula is L{u(t−a)} = e^{-as}/s.
What do the parameters in this formula mean?
Great question! Here, 'e^{-as}' represents the damping factor due to the delay in the system's response starting at time a, and 's' aids in understanding the frequency domain.
How does this help with engineering problems?
The transform allows engineers to analyze systems that have sudden load changes, such as impact loads on structures, helping to predict responses efficiently.
Can you give an example of when we might use this?
Certainly! For example, if a bridge experiences a sudden load from passing vehicles, we can model that force as a step function starting from the time the vehicle reaches the bridge.
So, it simplifies calculations?
Yes! Utilizing the Laplace transform simplifies the mathematics involved, making it easier to solve complex differential equations related to structural principles.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the definition and application of the Unit Step Function u(t−a), which transitions from 0 to 1 at t=a. It outlines its significance in performing Laplace transforms on piecewise functions and discusses how it represents delayed responses in systems.
Detailed
Unit Step Function u(t−a)
The Unit Step Function, denoted as u(t−a), is a crucial concept in engineering mathematics and Laplace transforms. It is defined mathematically as:
$$
u(t - a) = \begin{cases} 0 & \text{if } t < a \ 1 & \text{if } t \geq a \end{cases}$$
This function effectively captures situations where a system experiences a sudden change at a specific moment, modeled at time t = a.
In the context of Laplace transforms, the step function helps with analyzing piecewise or discontinuous functions that are prevalent in civil engineering scenarios, such as step loads and transient response systems.
Laplace Transform of the Unit Step Function
The Laplace transform of u(t−a) is given by:
$$L{u(t−a)} = \frac{e^{-as}}{s}$$
This representation is significant when considering the effects of delayed forces or actions in structural systems, allowing engineers to appropriately model and calculate dynamic responses to impacts or inputs that have a specific start time.
Youtube Videos
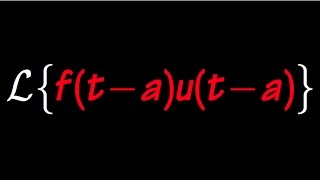
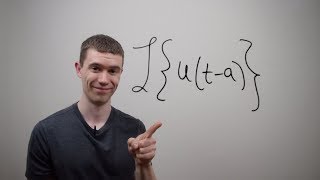
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Unit Step Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Unit Step Function, denoted as u(t−a), is defined as:
\[ u(t−a) = \begin{cases} 0 & \text{if } t < a \
1 & \text{if } t \geq a \end{cases} \]
Detailed Explanation
The Unit Step Function is a mathematical function that switches values at a certain point, defined by 'a'. For any time 't' that occurs before 'a', the function outputs 0, indicating that no response has occurred before this critical time. Once 't' reaches 'a' or any time thereafter, the function outputs 1, indicating a full response or activation. This behavior is useful in modeling systems that turn on or change states at a specific time.
Examples & Analogies
Imagine a light switch in a room. When the switch is off (similar to how 't' is less than 'a'), the room stays dark (the output is 0). Once you flip the switch on at a certain moment (when 't' equals 'a'), the lights turn on, and the room becomes lit (the output switches to 1).
Laplace Transform of the Unit Step Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Laplace Transform of the Unit Step Function is given by:
\[ L\{u(t−a)\} = \frac{e^{-as}}{s} \]
Detailed Explanation
The Laplace Transform is a technique used to convert functions from the time domain into the frequency domain. For the Unit Step Function, the result of its Laplace Transform involves an exponential decay factor 'e^{-as}' divided by 's'. This formula indicates how the step function contributes to the Laplace Domain, emphasizing the role of 'a' as a shift in time and 's' as the variable in the Laplace space. This transform is particularly useful in engineering applications where systems start at a delayed time.
Examples & Analogies
Consider a factory that starts operations at a scheduled time 'a'. The production rates could be represented by u(t−a). In the Laplace Transform domain, when we analyze factors like setup time and delay in production distribution, we see how this initial delay affects operations using our formula. The term 'e^{-as}' captures the essence of the delay in starting production while providing a mathematical framework to analyze the system's responsiveness.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Unit Step Function: A function that models discontinuous actions in engineering, switching between two states.
-
Laplace Transform: A method to convert time-domain functions into frequency-domain representations, facilitating easier problem solving.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Unit Step Function can model the sudden application of a load, like a weight dropped on a beam at a certain time.
-
In a simple electrical circuit, a switch that turns on at a certain time can be represented using the Unit Step Function.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When t is less, the step won't press, at a equals one, the change has begun.
📖 Fascinating Stories
-
Imagine a light switch that nobody can touch but at a specific moment, it turns on, illuminating everything instantly—this is like the Unit Step Function.
🧠 Other Memory Gems
-
Remember 'Step = Shift' for understanding how the Unit Step Function shifts from inertia to action.
🎯 Super Acronyms
U.S.F. stands for Unit Step Function - it tells you when the action starts (U) and what it does (S to F).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Unit Step Function
Definition:
A mathematical function u(t−a) that transitions from 0 to 1 at t=a, representing sudden changes or actions in systems.
-
Term: Laplace Transform
Definition:
An integral transform that converts a function of time into a function of a complex variable, used broadly in engineering to solve differential equations.