Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Groundwater Flow
Unlock Audio Lesson
Today, we're going to explore groundwater flow and its significance within civil engineering. Groundwater is a crucial resource, and understanding its flow helps in managing water resources effectively.
Why is it important to study groundwater flow specifically?
Great question! Groundwater flow directly affects water supply, aquifer sustainability, and environmental management. Knowing how it behaves allows us to create better management strategies.
Are there specific equations used to describe this flow?
Absolutely! The key equations are Darcy's law and the continuity equation.
Can you remind us what Darcy's law states?
Of course! Darcy's law describes the flow of fluid through a porous medium. It states that the flow rate is proportional to the hydraulic gradient.
That sounds pretty useful in practice!
It is indeed! Understanding these principles helps us address real-world issues in fluid mechanics.
Laplace Transforms in Groundwater Flow
Unlock Audio Lesson
Now, let's delve into how Laplace transforms can simplify our work with groundwater flow.
How do they help with unsteady flow equations?
Great question! They convert complex differential equations into algebraic equations, making them easier to solve.
And these equations are derived from Darcy's law too, right?
Exactly! The transformations help us analyze equations that describe transient flow conditions.
Are there examples of these equations in action?
Yes, the applications range from predicting groundwater movement under various conditions to designing effective wells.
That makes it clear how vital these concepts are in engineering!
Absolutely! Applying mathematics like Laplace transforms is essential for effective engineering practice.
Real-world Applications
Unlock Audio Lesson
Now that we understand the theory, let’s discuss real-world applications of our findings.
Can you give us an example?
Sure! One application is in designing drainage systems. By modeling groundwater flow, we can predict how water moves through soil and plan accordingly.
What about pollution control?
Excellent point! Understanding flow dynamics helps design better containment strategies for pollutants, preventing groundwater contamination.
How do engineers validate their models?
They often use field data to calibrate their models. This ensures that theoretical predictions align with actual observations.
I can see how important this knowledge is for sustainability!
Exactly! It's about marrying theory with practice to make informed engineering decisions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the focus is on how Laplace transforms facilitate the analysis of unsteady flow equations governed by Darcy's law and continuity equations, which are crucial for understanding groundwater movement and fluid mechanics in civil engineering applications.
Detailed
Groundwater Flow and Fluid Mechanics
In civil engineering, particularly concerning groundwater flow and fluid mechanics, the use of Laplace transforms is indispensable for solving complex unsteady flow equations. This section emphasizes the importance of utilizing Laplace transforms to analyze groundwater flow dynamics effectively. The core equations governing this flow, including Darcy's law and continuity equations, describe how fluids move through porous media.
These mathematical tools not only streamline calculations but also enhance the understanding of fluid behavior under varied conditions. By transforming differential equations into algebraic forms, engineers can more quickly and effectively predict the movement of groundwater, assess aquifer behavior, and develop appropriate hydraulic models. The versatility of Laplace transforms in handling initial value problems related to transient flow lingers as a key takeaway, enriching the practical applications of mathematics in addressing real-world engineering challenges.
Youtube Videos
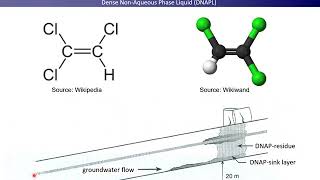
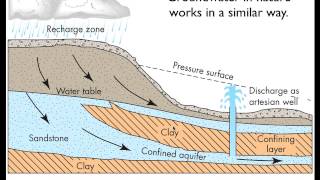
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Groundwater Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Laplace transforms solve unsteady flow equations governed by Darcy's law and continuity equations.
Detailed Explanation
This chunk introduces how Laplace transforms can be applied to the equations governing groundwater flow. Specifically, it mentions two key principles: Darcy's law, which describes the flow of fluid through porous media, and the continuity equation, which ensures that mass is conserved in the flow. The use of Laplace transforms helps in solving these equations, especially when dealing with complex, time-dependent scenarios.
Examples & Analogies
Imagine a sponge soaking up water. The rate at which water moves through the sponge represents flow, similar to what Darcy's law describes. Now, suppose you want to understand how quickly the sponge can soak up water if you suddenly increase the water level above it. By using Laplace transforms, engineers can predict how the flow changes over time, just as you might predict how quickly water disappears into the sponge at different levels.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Darcy's Law: Describes the flow rate of a fluid through porous media.
-
Continuity Equation: Represents the conservation of mass for fluids.
-
Unsteady Flow: Describes fluid flow that varies with time.
-
Laplace Transform: A powerful tool to analyze systems governed by differential equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Laplace transforms to solve groundwater flow equations that account for varying hydration conditions.
-
Applying Darcy's law to model how water flows through different soil types.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flowing water deep underground, keeps crops alive all year 'round.
📖 Fascinating Stories
-
A farmer named Joe used to struggle with crops till he learned about groundwater flow. Now, he knows how to water his fields perfectly by understanding the movement of water beneath the surface.
🧠 Other Memory Gems
-
To remember Darcy's Law, think: 'Fluid Flows Fast' – Fluid, Flow rate, Fast through the medium.
🎯 Super Acronyms
DOL - Darcy's law, Outflow, Law of flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Groundwater Flow
Definition:
The movement of water beneath the Earth's surface through soil and rock formations.
-
Term: Darcy's Law
Definition:
A mathematical equation relating the flow rate of a fluid through a porous medium to the hydraulic gradient.
-
Term: Continuity Equation
Definition:
An equation that represents the conservation of mass in fluid dynamics, showing the relationship of fluid flow at different points.
-
Term: Laplace Transform
Definition:
A mathematical transform that converts a function of time into a function of a complex variable, facilitating the analysis of linear systems.