Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Transition from Fourier to Laplace
Unlock Audio Lesson
Welcome class! Today, we are going to discuss the modified version of the Fourier transform, which is the Laplace transform. Now, can anyone tell me why we might need to use Laplace transforms in addition to Fourier transforms?
Is it because there are functions that don't work well with Fourier transforms?
Exactly! Fourier transforms require functions to be integrable over the entire real line. In contrast, Laplace transforms are much more flexible. They can handle functions that are not absolutely integrable, including those that are discontinuous or grow exponentially.
Could you give an example of such a function?
Sure! An example is the step function, common in engineering applications for modeling sudden loads. These kinds of functions can be challenging for Fourier transforms but are easily handled by Laplace transforms.
So, it sounds like Laplace transforms help especially with initial-value problems?
Exactly! They are great for solving ordinary differential equations with initial conditions. Let’s move on to how the Laplace transform is defined mathematically.
Mathematical Foundation of Laplace Transform
Unlock Audio Lesson
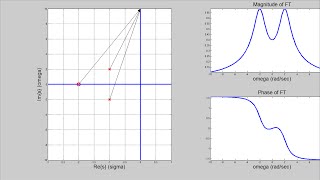
The Laplace transform of a function f(t) defined for t ≥ 0 is given by the integral of e^{-st}f(t). Does anyone know what s represents?
Isn't s a complex number composed of a real part σ and an imaginary part ω?
Correct! s = σ + iω. This means we have a damping factor e^{-σt} that influences convergence. Can anyone tell me why the damping factor is important?
It helps the integral converge better, especially for functions that grow too fast!
Exactly! Now, remember that when we set s = iω in the Laplace transform, we essentially recover the Fourier transform under some conditions. Let’s think about that in applications next.
Applications of the Laplace Transform
Unlock Audio Lesson
Now let's discuss some applications where the Laplace transform shines because of its modified properties. Who can mention an engineering scenario where we rely on it?
Structural vibration analysis? We often have to deal with differential equations there!
Great example! The Laplace transform simplifies these differential equations. Do you recall how we can turn our function analyses into algebraic equations using Laplace transforms?
By transforming the differentials into polynomials in s?
You got it! This is why Laplace transforms are integral to transient analyses such as in heat conduction and fluid dynamics. Can anyone think of a possible disadvantage?
Maybe that it's complex to understand when initially learning? But the benefits outweigh that, right?
Absolutely! The initial learning curve can be steep, but the flexibility and power they offer are invaluable. Let’s summarize what we’ve learned today about the Laplace transform.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
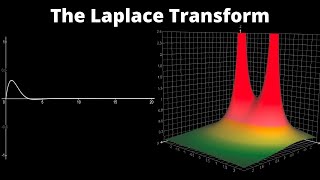
This section explores the connection between Laplace and Fourier transforms by expressing the Laplace transform as a Fourier transform with an exponential damping factor. This modification allows for handling functions that are not absolutely integrable or that exhibit discontinuities, making it particularly useful in engineering applications.
Detailed
In the context of engineering mathematics, the Laplace transform is seen as a modified form of the Fourier transform. More specifically, the Laplace transform can be expressed as a Fourier transform of the exponentially damped function e^{-σt}f(t), where σ is a real number that introduces a damping effect. This modification ensures improved convergence for functions that may not be absolutely integrable over the entire real line. The significance of this relationship lies in the ability of Laplace transforms to effectively handle discontinuous, exponentially growing functions and solve initial-value problems in ordinary differential equations. This enhancement positions Laplace transforms as critical tools in various engineering applications, allowing for the analysis and resolution of complex systems defined in causal terms.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Laplace Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let:
Z ∞ Z ∞
F(s)= e−stf(t)dt= e−σte−iωtf(t)dt
0 0
Detailed Explanation
The Laplace transform of a function f(t) is defined by the integral that looks at the weighted values of f(t) as time progresses. The equation shows that we take f(t) and multiply it by two exponential factors: e^{-σt} and e^{-iωt}. The first factor, e^{-σt}, serves as a damping term, which allows us to analyze functions that grow exponentially or are not well-behaved at infinity. This dual exponential structure links the Laplace transform to concepts in Fourier transforms, introducing a way to manage convergence for non-periodic functions.
Examples & Analogies
Imagine you’re listening to a piece of music over time. Just like how different notes can fade out (damping) and how multiple instruments can be layered together, the Laplace transform captures the essence of the function you're analyzing by 'dampening' its behavior over time while also incorporating its oscillatory characteristics, like the elements of a musical score coming together.
Exponential Damping for Improved Convergence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This can be viewed as a Fourier transform of the function e−σtf(t), provided the function is exponentially bounded. Hence, the Laplace transform introduces a damping factor e−σt, which improves convergence.
Detailed Explanation
The key benefit of the Laplace transform is that it introduces the exponential damping factor, e^{-σt}. This factor ensures that as t approaches infinity, the contributions of f(t) diminish and result in better convergence of the integral. This is particularly useful in engineering applications where functions may grow too large to be handled using ordinary Fourier transforms, which would treat them as oscillations without addressing their growth issues. Exponential damping therefore enhances the scope of problems we can solve using the Laplace transform.
Examples & Analogies
Think of a hot cup of coffee left in an open room. Over time, its heat will dissipate and it will cool down, making it harder to sip directly after being scalding hot. The damping factor is like the cooling effect—just as your coffee slowly settles into a more manageable temperature, the exponential factor helps ensure that functions behaving wildly as time goes on become easier to analyze and control.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
The relationship between Laplace and Fourier transforms.
-
The role of the damping factor in Laplace transformations.
-
Applications of Laplace transforms in engineering and initial-value problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing a step function is easier with Laplace transforms due to their ability to address discontinuities.
-
Transforming a structural vibrational differential equation into an algebraic equation in the s-domain allows for simpler solutions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Laplace transforms with damping bring, smoother paths for the function to sing.
📖 Fascinating Stories
-
Picture an engineer faced with a differential equation representing a shaky bridge. They apply the Laplace transform, introducing a damping factor like a safety net, bringing stability and clarity to the once daunting problem.
🧠 Other Memory Gems
-
To remember the steps of using Laplace transforms: L = Leads to Algebra, P = Polynomial insights.
🎯 Super Acronyms
LTD
- Laplace Transforms Dampen — remember that they make tough functions manageable!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Laplace Transform
Definition:
An integral transform that converts a function of time into a function of a complex variable, typically used for analyzing linear time-invariant systems.
-
Term: Damping Factor
Definition:
A factor, e^{-σt} in the Laplace transform, that helps improve convergence for functions that are not absolutely integrable.
-
Term: Fourier Transform
Definition:
A mathematical transform used to express a function as a sum of periodic components, often used for functions defined over the entire real line.
-
Term: Initial Value Problems
Definition:
Problems involving differential equations which require solutions that satisfy specified values at the start or initial point.
-
Term: Exponential Growth
Definition:
A situation where a quantity increases at a consistent rate over time, posing challenges for certain transforms.