Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Fourier Cosine Transform Fundamentals
Unlock Audio Lesson
Today, we are going to dive into the Fourier Cosine Transform. Can anyone tell me what a transform does?
It helps convert functions into a different domain, often making them easier to work with!
Exactly! The Fourier Cosine Transform specifically helps us analyze even functions. It is defined as the integral of the function multiplied by cosine. The formula is: F_c(ω) = ∫₀^∞ f(x) cos(ωx) dx.
Could you remind us why we use cosine?
Great question! Cosine functions are even, which aligns perfectly with the properties of the functions we analyze using the FCT. Remember: E_c = Even + Cosine.
What about its inverse? How do we get back the original function?
The inverse is just as important! It is written as f(x) = (2/π) ∫₀^∞ F_c(ω) cos(ωx) dω. This allows us to recover the original function after applying the transform.
So, it's a two-way street. We can go from function to transform and back again!
Precisely! To summarize, the Fourier Cosine Transform is defined for even functions to simplify analysis and can be inverted to retrieve the original function.
Fourier Sine Transform Fundamentals
Unlock Audio Lesson
Now that we've covered the Fourier Cosine Transform, let's switch gears to the Fourier Sine Transform. Who can tell me how it's defined?
Isn't it similar, but with sine instead?
Absolutely! The Fourier Sine Transform is defined as F_s(ω) = ∫₀^∞ f(x) sin(ωx) dx. Sine functions are odd, which helps us analyze odd functions effectively.
Oh! So we have E_s = Even + Sine and O_s = Odd + Sine?
Well said! The inverse of the Fourier Sine Transform allows us to recover the original function using the formula: f(x) = (2/π) ∫₀^∞ F_s(ω) sin(ωx) dω.
How would we apply these transforms in real-world problems?
These transforms are powerful tools for solving partial differential equations in applications like heat conduction and wave propagation, particularly in scenarios involving semi-infinite domains. Understanding both transforms helps us see the full picture!
Got it! So each transform has its specific use depending on whether the function is even or odd.
Exactly! To summarize, the Fourier Sine Transform is defined for odd functions and serves a crucial role alongside the Cosine Transform in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the formulations for the Fourier Cosine Transform (FCT) and the Fourier Sine Transform (FST), detailing their definitions, inverse transformations, and their applicability in engineering problems involving semi-infinite domains.
Detailed
Fourier Cosine and Sine Transforms
In this section, we explore the Fourier Cosine Transform (FCT) and the Fourier Sine Transform (FST), both of which are integral transformations that extend the capabilities of Fourier analysis into semi-infinite domains. These transforms are particularly useful in solving partial differential equations (PDEs).
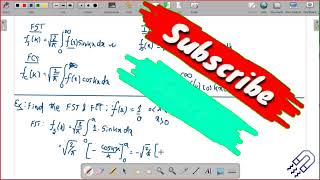
Fourier Cosine Transform (FCT)
The FCT is defined as:
\[ F_c(\omega) = \int_0^{\infty} f(x) \cos(\omega x) dx \]
The inverse Fourier Cosine Transform is given by:
\[ f(x) = \frac{2}{\pi} \int_0^{\infty} F_c(\omega) \cos(\omega x) d\omega \]
The FCT is useful for handling boundary value problems that are even functions.
Fourier Sine Transform (FST)
The FST can be defined similarly:
\[ F_s(\omega) = \int_0^{\infty} f(x) \sin(\omega x) dx \]
Its inverse transformation is:
\[ f(x) = \frac{2}{\pi} \int_0^{\infty} F_s(\omega) \sin(\omega x) d\omega \]
The FST is particularly suited for odd functions.
Together, the Fourier Cosine and Sine Transforms provide powerful tools for analyzing and solving PDEs over semi-infinite domains, making them fundamental in engineering applications involving wave propagation, heat conduction, and more.
Youtube Videos
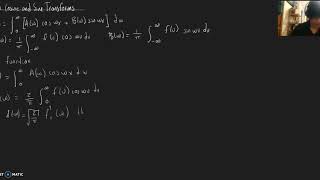
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Cosine Transform (FCT)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Z ∞
F (ω)= f(x)cos(ωx)dx
c
0
Inverse:
2 Z ∞
f(x)= F (ω)cos(ωx)dω
π c
0
Detailed Explanation
The Fourier Cosine Transform (FCT) is defined as an integral that transforms a function f(x) into a function F(ω). It combines the values of f(x) with a cosine function, effectively analyzing the function's frequency components for non-negative frequencies. The formula captures how f(x) changes over time, weighted by the cosine of the frequency ω. The inverse of the Fourier Cosine Transform reconstructs the original function f(x) from the transformed function F(ω) using the same cosine function over the range of ω.
Examples & Analogies
Think of the Fourier Cosine Transform as a music mixer. If f(x) is a music track and the cosine represents different instruments, the FCT analyzes how much of each instrument is present at different frequencies. When listening back to the track, the inverse FCT is like playing the mix again, reconstructing the original song from the frequencies captured.
Fourier Sine Transform (FST)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Z ∞
F (ω)= f(x)sin(ωx)dx
s
0
Inverse:
2 Z ∞
f(x)= F (ω)sin(ωx)dω
π s
0
Detailed Explanation
The Fourier Sine Transform (FST) transforms a function f(x) using sine functions instead of cosine functions. It captures the sine-weighted frequency information of f(x) for non-negative frequencies. The inverse process allows us to recover the original function f(x) from the sine-transformed function F(ω) by integrating over the range of ω. This transform is particularly useful for analyzing odd functions or signals that represent physical systems extending to infinity in one direction.
Examples & Analogies
Imagine you are studying the vibrations of a guitar string. The FST helps you understand how the string vibrates at different frequencies, represented by the sine waves. When you pluck the string and hear the sound, the inverse FST lets you recreate the vibrations from the frequency information we've captured, much like reconstructing a melody from its notes.
Applications of Fourier Transforms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These transforms are particularly useful for solving partial differential equations (PDEs) in semi-infinite domains.
Detailed Explanation
Fourier transforms, including both the cosine and sine transforms, are vital techniques in engineering and mathematics used to solve partial differential equations (PDEs). In semi-infinite domains—such as heat diffusion in a rod that is infinitely long—these transforms simplify the complex relationships of the variables involved, allowing engineers to find approximate solutions to real-world problems in heat conduction, fluid flow, and structural analysis.
Examples & Analogies
Consider heating one end of a long metal rod. The temperature distribution along the rod over time can be complicated to model using regular equations. By applying Fourier transforms, we can break down this problem into manageable parts, finding solutions step by step. This is like resolving a complicated traffic pattern into simpler routes for easier navigation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Cosine Transform: An integral that transforms functions in semi-infinite domains using cosine, useful for even functions.
-
Fourier Sine Transform: An integral that transforms functions in semi-infinite domains using sine, useful for odd functions.
-
Inverse Transform: The operation by which the original function can be recovered from its transformed state.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Fourier Cosine Transform can be used to simplify solving a heat equation on a semi-infinite rod.
-
The Fourier Sine Transform can analyze the displacement of a beam subjected to a dynamic load, particularly when the load's influence is odd in nature.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Cosine for even, Sine for odd,
🎯 Super Acronyms
COS for 'C'osine, & ODD for 'S'ine!
📖 Fascinating Stories
-
Imagine engineers trying to solve the riddle of a structure; with even functions, they can use cosine transforms like a hidden key unlocking the door to solutions!
🧠 Other Memory Gems
-
E_c = Even + Cosine, O_s = Odd + Sine.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Cosine Transform
Definition:
An integral transform of a function defined over a semi-infinite domain, using the cosine function, useful for even functions.
-
Term: Fourier Sine Transform
Definition:
An integral transform of a function defined over a semi-infinite domain, utilizing the sine function, appropriate for odd functions.
-
Term: Integral Transform
Definition:
A mathematical operation that converts a function into another domain, simplifying analysis and problem-solving.