Convolution Theorem for Laplace Transforms
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Convolution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the Convolution Theorem in the context of Laplace transforms. First, can anyone tell me what convolution means?

Isn't convolution a way to combine two functions together?

Exactly, well done! Convolution, symbolized as * , allows us to combine two functions, say f(t) and g(t), in a specific integral form. It helps us find outcomes in systems influenced by multiple inputs over time.

How does that relate to Laplace transforms?

Great question! The Laplace transform allows us to analyze convolutions in the frequency domain. We will see that the Laplace of a convolution simplifies to the product of their respective Laplace transforms.

So it’s like transforming functions to a different 'language' to make calculations easier?

Precisely! That's a wonderful analogy. We will get into the nitty-gritty details shortly.

Let’s recap: convolution combines two functions, and it plays a vital role in simplifying our calculations when using Laplace transforms.
Mathematical Definition of Convolution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s look at the mathematical definition of convolution. The convolution of two functions f(t) and g(t) is defined as:

The formula is $$ (f * g)(t) = \int_0^t f(\tau) g(t - \tau) d\tau $$ Can anyone explain the significance of this integral?

It seems like we're summing the products of the functions over time, right?

Yes! This integral takes product values of f and g, considering their influences over time, which can be very useful in system analysis.

I get that! So if I change either function, it changes the result of the convolution?

Exactly, so it reflects how each function affects the system's overall output.

Key takeaways: Convolution combines functions over time and reveals output influenced by multiple inputs.
Application of the Convolution Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's talk about how we apply the Convolution Theorem in practical scenarios. Why is this theorem useful in systems analysis?

It probably helps when we have complex systems with different functions acting together.

Spot on! Especially in engineering, where we often encounter systems excited by multiple inputs, this theorem helps in simplifying computations.

Can you give us an example of when we would use this?

Sure! In control systems, if we have a system response described by f(t) and we apply a force described by g(t), the resulting system output can be calculated using the convolution of these two inputs.

So it’s really powerful for solving differential equations too, right?

Yes! Remember, convolution is a key tool in inverse Laplace techniques, providing the means to retrieve time-domain results from the transformed domain.

To summarize, the Convolution Theorem allows us to efficiently handle multiple inputs in systems by simplifying their combined outcome in the Laplace domain.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the Convolution Theorem for Laplace Transforms, highlighting how it defines the convolution of two functions f(t) and g(t) and states that the Laplace transform of this convolution equals the product of the Laplace transforms of the individual functions. It emphasizes the practical application of this theorem in systems analysis and inverse Laplace techniques.
Detailed
Convolution Theorem for Laplace Transforms
The Convolution Theorem is a fundamental result in the study of Laplace transforms. It provides a powerful method for handling the multiplication of functions in the Laplace domain. Specifically, for functions defined on positive time, the convolution of two functions, f(t) and g(t), is defined as:
$$
(f * g)(t) = \int_0^t f(\tau) g(t - \tau) d\tau
$$
This integral captures the idea of combining two functions across time, representing how the output of a system is influenced by two different inputs over time.
The key conclusion of the theorem is:
$$
L\{(f * g)(t)\} = F(s) \cdot G(s)
$$
where L denotes the Laplace transform, and F(s) and G(s) are the Laplace transforms of f(t) and g(t), respectively. This relationship simplifies the analysis of systems where direct transformation might be complex, making the Convolution Theorem an essential technique for engineers and mathematicians alike, particularly in fields such as control systems and signal processing.
Youtube Videos



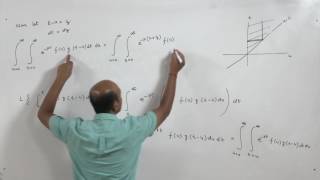





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Convolution
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The convolution of two functions f(t) and g(t) is defined as:
$$
(f ∗ g)(t) = \int_0^t f(\tau) g(t - \tau) d\tau
$$
Detailed Explanation
In mathematics, the convolution of two functions is a way of combining them to form a third function. Specifically, it involves integrating the product of the two functions, where one function is 'flipped' and shifted. The formula shows that the convolution (f * g)(t) is obtained by integrating the product of f(\tau) and g(t - \tau) from 0 to t. This means that for every point in time t, we are summing the products of f and g shifted over one another.
Examples & Analogies
Imagine you are making a sandwich. The bread is one function, f, and the filling is another function, g. As you spread the filling onto the bread, you want it to evenly cover each slice. The convolution represents this process where you take each point of the bread (f) and pair it with the corresponding point of the filling (g), creating a full sandwich that combines both elements.
Laplace Transform of Convolution
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Then,
$$
L{(f ∗ g)(t)} = F(s) · G(s)
$$
Detailed Explanation
The Laplace Transform applies a powerful mathematical operation that converts functions from the time domain (where they are expressed as functions of time) to the s-domain (a complex frequency domain). According to the Convolution Theorem, the Laplace Transform of the convolution of two functions, (f * g)(t), is equal to the product of their individual Laplace Transforms, F(s) and G(s). This theorem is particularly valuable because it simplifies the process of analyzing systems and solving differential equations.
Examples & Analogies
Think of the convolution theorem like a team project. If you want to assess the overall efficiency (the Laplace Transform) of your project (the convolution) using individual performances (F(s) and G(s)), multiplying the performance ratings of each member helps you understand the project outcome much faster than evaluating each contribution separately.
Applications of the Convolution Theorem
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This theorem is highly useful in systems analysis and inverse Laplace techniques, particularly when direct transformation is difficult.
Detailed Explanation
The convolution theorem provides critical assistance in many areas of analysis, such as control systems, signal processing, and differential equations. When dealing with complex functions where directly applying the Laplace Transform may be challenging, this theorem allows analysts to simplify the process by converting convolutions into products in the s-domain. This facilitates easier manipulations and solutions.
Examples & Analogies
Consider a baker trying to find the best recipe for a cake that balances sweetness and creaminess. If the baker could use the 'recipe' for sweetness (function F) and the 'recipe' for creaminess (function G) separately, it makes finding the perfect blend (the convolution result) much simpler than trying to figure it out by simply mixing random amounts of each ingredient together, analogous to direct transformations that might not work well.
Key Concepts
-
Convolution: A fundamental operation combining two functions relevant in Laplace transforms.
-
Laplace Transform: Tool for transforming functions in the time domain to the frequency domain.
Examples & Applications
An example of convolution could be the response of a system to multiple forces applied over time.
In signal processing, if the input signal is f(t) and the system's impulse response is g(t), the output can be computed using convolution.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When functions combine, and the sum's aligned, convolution is the key, to see how they entwined.
Stories
Imagine two rivers converging into one. Their paths twist and turn together, reflecting each other's strengths. Just as the rivers merge, two functions combine through convolution to reveal their joint influence.
Memory Tools
FISH - Functions Integrate to Sum harmoniously.
Acronyms
CALS - Convolution And Laplace Simplified.
Flash Cards
Glossary
- Convolution
A mathematical operation that combines two functions to produce a third function, representing how the shape of one is modified by the other.
- Laplace Transform
An integral transform used to convert a function of time into a function of a complex variable, often used for analyzing linear time-invariant systems.
Reference links
Supplementary resources to enhance your learning experience.
