First Shifting Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the First Shifting Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will discuss the First Shifting Theorem, which is a powerful tool when working with Laplace transforms. It relates the transformation of a modified function to its original form.

Can you explain what this theorem actually states?

Of course! The theorem states that the Laplace transform of `e^{at} f(t)` equals `F(s-a)`, where `F(s)` is the Laplace transform of `f(t)`. This effectively shifts the transform in the frequency domain.

Why is this shift important?

Great question! The shift accounts for the exponential growth or decay in our functions, making it essential for analyzing systems like circuits and mechanical systems under such conditions.

Is this theorem used often in applications?

Yes, absolutely! It's used widely in engineering applications, especially in control systems and differential equations involving exponential terms.

To recap, the First Shifting Theorem allows us to transform a function multiplied by an exponential into a shifted form, simplifying our analysis of exponentially influenced systems.
Applying the First Shifting Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at an example. If we have `f(t) = t^2` and we want to find `L{e^{3t}t^2}`.

So we should first find the Laplace transform of `t^2` and then apply the shift?

Exactly! The Laplace transform of `t^2` is `2/s^3`. Using the First Shifting Theorem, we would shift it by 3 units. Thus, we get `L{e^{3t}t^2} = 2/(s-3)^3`.

What if we have a different function? Would the process change?

The process remains the same! No matter the function, you find its Laplace transform first, then apply the shift based on the multiplier.

Can we summarize the steps for using this theorem?

Certainly! First, find the Laplace transform of `f(t)`, then replace `s` in `F(s)` with `s - a` where `e^{at}` was your multiplier. It’s that straightforward!
Concept Reinforcement and Critical Thinking
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s think critically. Why do we need to shift the Laplace transform when there's an exponential multiplier?

It makes sense because the exponential part influences the frequency response of the system, right?

Exactly! The shift captures how quickly or slowly the function behaves over time, which is vital for control systems.

Can you provide another real-world example where this may apply?

Certainly! In electrical engineering, when analyzing circuits under exponential time-variant inputs, the First Shifting Theorem is critical to correctly finding circuit responses.

So, it’s very essential for modelling transient states?

Precisely! In transient states where the behavior changes quickly, capturing the exponential influences is vital, and the First Shifting Theorem allows us to do that efficiently.

To summarize, the First Shifting Theorem not only shifts the Laplace transform but also captures essential system behaviors, which are crucial for engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The First Shifting Theorem states that the Laplace transform of the product of an exponential function and another function results in a shift in the s-domain by that exponential's growth rate. This theorem is vital for analyzing systems with exponential growth or decay.
Detailed
First Shifting Theorem
The First Shifting Theorem (also known as the first shifting property) is a fundamental property of the Laplace transform useful for solving differential equations with exponential terms. The theorem is stated as:
L{e^{at} f(t)} = F(s-a)
Here, L denotes the Laplace transform operator, e^{at} is an exponential function, f(t) is a function, and F(s) is the Laplace transform of f(t). This theorem shows how multiplying a function by an exponential term shifts its Laplace transform in the complex frequency domain.
Significance
This theorem simplifies the process of transforming equations involving exponential growth or decay, such as those encountered in engineering applications related to control systems and circuit analysis, making it easier to find solutions for systems with such behaviors.
Youtube Videos






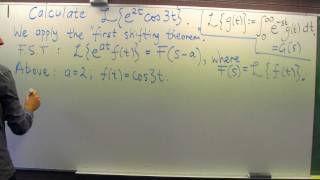
![Inverse Laplace transformation Lec-14 First shifting property L^-1[(s+8)/(s^2+4s+16)]](https://img.youtube.com/vi/ii_R0s_dKxo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the First Shifting Theorem
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
L{eatf(t)}=F(s−a)
Detailed Explanation
The First Shifting Theorem applies to the Laplace Transform. It states that if you have a function f(t) multiplied by an exponential function eat, multiplying by e to the power of at shifts the Laplace Transform of f(t). When you find the Laplace Transform of this modified function, it results in F(s - a), where F(s) is the original Laplace Transform of f(t). Essentially, you're adjusting the variable s in the Laplace Transform by subtracting 'a'. This helps to simplify the analysis of functions affected by exponential growth or decay.
Examples & Analogies
Consider the scenario of a light bulb that gradually brightens over time, accelerating its brightness by a factor of 'a' every unit of time. If we represent the brightness function as f(t), the First Shifting Theorem tells us how to find the transformed version of this function with respect to the exponential growth. Just like adjusting the brightness setting on your screen, you adjust the Laplace transform to account for real-world changes over time.
Key Concepts
-
First Shifting Theorem: Relates the Laplace transform of an exponentially scaled function to a shifted version of the function's transform.
-
Laplace Transform: A mathematical tool used to facilitate the analysis of linear systems by transforming differential equations into algebraic equations.
Examples & Applications
If f(t) = t^2, then L{e^{3t}t^2} = 2/(s-3)^3.
For a function f(t) = sin(t), using the theorem, L{e^{2t}sin(t)} would yield a shift and give F(s-2) corresponding to sin(t).
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When exponentials meet Laplace's grace, in s-a, we shift the pace.
Stories
Imagine an engineer solving a circuit problem, and discovering that when they use an exponential function, it magically shifts their solve point by the exponential's rate, making complex problems manageable.
Memory Tools
For shifts, remember the phrase: Exponential times, minus the rate allows the function to equate.
Acronyms
E.F.S = Exponential Function Shift
Identifies the need for shifting in Laplace transform contexts.
Flash Cards
Glossary
- First Shifting Theorem
A property of the Laplace transform defining that the Laplace transform of
e^{at} f(t)isF(s-a), resulting in a shift byain the s-domain.
- Laplace Transform
An integral transform used to convert a function of time into a function of a complex variable, facilitating the analysis of linear time-invariant systems.
Reference links
Supplementary resources to enhance your learning experience.
