Fourier Transform in PDEs
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Transform in PDEs
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into Fourier Transforms, a powerful method to solve certain types of Partial Differential Equations, particularly in infinite domains. Can anyone tell me what a Partial Differential Equation is?

Isn't it an equation that involves partial derivatives of a function with respect to multiple variables?

Exactly! PDEs incorporate functions with several independent variables. Now, why do you think Fourier Transforms might be useful here?

Could it be because they help break down complex functions into simpler sine and cosine components?

Precisely! This simplification is why they are so valuable in engineering applications. Remember, Fourier Transforms allow us to handle infinite or periodic domains effectively.

Can you give us an example?

Sure! The heat equation is a perfect example. It relates the temperature of an object over time, allowing us to understand heat distribution.

Could we visualize that heat distribution?

Great question! By applying a Fourier Transform, we can transform the spatial dimensions into frequency space, making analysis more manageable. Let’s recap: Fourier Transforms help us simplify PDEs, especially when dealing with infinite domains, such as in heat equations.
Applying Fourier Transform to the Heat Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s explore how we actually apply the Fourier Transform to the heat equation. Who can recall the form of the heat equation?

It's \( \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} \).

Well done! When we apply the Fourier Transform to this equation, we handle the spatial variable. What do we obtain?

We transform it into an ordinary differential equation over time, right?

Yes, that's correct! The transformation converts the PDE into an easier-to-solve ODE in terms of time. This means we can analyze solutions in terms of frequencies now.

And we would then revert to the original function using an inverse Fourier Transform?

Exactly! It’s all about moving back and forth between the time and frequency domains. Let’s summarize what we’ve discussed: Applying Fourier Transform allows us to turn complex PDEs into simpler ODEs, paving the way for effective engineering solutions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the application of Fourier Transforms in solving Partial Differential Equations (PDEs) is discussed, particularly in contexts involving infinite or periodic domains. The usefulness of Fourier Transform techniques in spatial signal analysis, exemplified through the heat equation, is emphasized.
Detailed
Fourier Transform in PDEs
The Fourier Transform is a powerful mathematical tool widely used in the field of engineering, especially for solving Partial Differential Equations (PDEs). This section discusses its application in problems characterized by infinite or periodic domains.
Key Points:
- Application Context: The Fourier Transform is particularly useful for analyzing spatial behaviors of signals or structures. It facilitates the solving of PDEs like the heat equation represented as:
\[ \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} \quad \text{for} \quad -\infty < x < \infty \]
- Process Overview: The standard procedure involves applying the Fourier Transform along the spatial variable (x-axis), which transforms the PDE into an ordinary differential equation (ODE) in time (t).
- Inverse Transform: After solving the ODE, the inverse Fourier Transform is applied to obtain the solution in the original spatial domain.
The significance of the Fourier Transform in PDEs cannot be understated, as it streamlines complex calculations and provides essential insights into physical systems, particularly in heat transfer analysis.
Youtube Videos
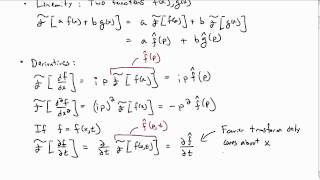
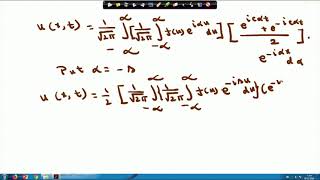







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fourier Transforms in PDEs
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Used in problems with:
- Infinite or periodic domains
- Spatial analysis of signals or structures
Detailed Explanation
Fourier transforms are mathematical tools used to analyze functions or signals. They are especially effective for problems that involve infinite or periodic domains, meaning they can easily manage situations where the behavior of a function extends indefinitely in one or more directions, or repeats cyclically. Additionally, Fourier transforms can be utilized for the spatial analysis of signals or structures, allowing engineers and scientists to understand how different frequencies contribute to the overall behavior of the system.
Examples & Analogies
Imagine a musician playing a complex piece of music. Each note corresponds to a different frequency and combines to create the overall sound. Similar to breaking music down into its individual notes to understand how they work together, engineers can use Fourier transforms to deconstruct signals or images in engineering analysis, leading to insights on how structures respond to various forces.
Example Application: The Heat Equation
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example: Heat equation ∂u/∂t = α∂²u/∂x² on −∞
Detailed Explanation
The heat equation is a fundamental partial differential equation (PDE) that describes how heat diffuses through a given region over time. In this context, the variable u represents the temperature, and the parameters indicate how fast the heat flows. By applying the Fourier transform to this equation along the spatial x-axis, we can transform the PDE into an ordinary differential equation (ODE) with respect to time, which is often easier to solve. After solving the ODE, we would use the inverse Fourier transform to convert our solution back into the spatial domain, thus arriving at u(x, t), which tells us about the temperature distribution over time in the given space.
Examples & Analogies
Think of this process like taking a panoramic photo of a landscape (Fourier transform). Once we have the panoramic overview (solving the ODE), we can decide to zoom in on a specific area to see fine details (inverse transform). This allows you to analyze the overall heat distribution in large spaces and understand how temperature behaves over an infinite expanse.
Key Concepts
-
Fourier Transform: A technique to express functions in terms of sine and cosine functions.
-
PDE: An equation involving partial derivatives of functions with several variables.
-
Inverse Transform: The process of deriving the original function from its transformed version.
Examples & Applications
Using Fourier Transform to solve the heat equation over infinite domains where temperature distribution is analyzed.
Transforming a given spatial problem into frequency space to extract insights about wave behaviors in signals.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the heat where temp’s in treat, transform with Fourier, it's really neat.
Stories
Imagine a blanket that spreads warmth. The Fourier Transform acts like a guide, showing how warmth travels through the blanket over time.
Memory Tools
Remember 'F4 PODE', where 'F' is for Fourier, '4' for transforms, 'P' for Partial, 'O' for Ordinary, 'D' for Differential, 'E' for Equations.
Acronyms
F-TIME (Fourier Transform In Modeling Equations) to recollect its significance in solving PDEs.
Flash Cards
Glossary
- Fourier Transform
A mathematical transform that decomposes a function into its constituent frequencies.
- Partial Differential Equation (PDE)
An equation that involves partial derivatives of a multivariable function.
- Ordinary Differential Equation (ODE)
An equation that describes a relationship involving functions of one independent variable and its derivatives.
- Heat Equation
A specific type of PDE that describes the distribution of heat over time.
- Inverse Fourier Transform
A transform that converts frequency domain data back into the time or spatial domain.
Reference links
Supplementary resources to enhance your learning experience.
