Defining the Laplace Transform
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Laplace Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore the Laplace transform. Can anyone tell me what a transform is in mathematics?

Isn't it a way to change a function from one form to another?

Exactly! The Laplace transform specifically changes a time-domain function into a complex frequency-domain function. Who can help define the Laplace transform mathematically?

It’s defined as an integral: F(s) = integral from 0 to infinity of e^-st times f(t) dt!

Well done! Remember that s is a complex number. This transform is useful in engineering for solving differential equations. We call it a tool for simplifying the analysis. Let's remember the acronym 'LIFT' for Laplace Integral for Function Transformation!
Importance and Applications of the Laplace Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about why the Laplace transform is so important. Can anyone think of the limitations of Fourier transforms?

They can't handle some functions that are not integrable over the entire real line?

That's correct! The Laplace transform overcomes those limitations by being able to manage functions that are defined only for t ≥ 0. It’s especially useful for studying systems in engineering that deal with initial value problems. Can anyone give me an example of where this might be applied?

Maybe in analyzing electrical circuits or mechanical systems?

Exactly! In both cases, the initial conditions of the systems can be captured effectively through the Laplace transform. Remember, it helps in simplifying our mathematics significantly!
Mathematical Structure of the Laplace Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dig deeper into the structure of the Laplace transform. What function does the term e^-st serve in the integral?

I think it acts as a damping factor that helps with convergence?

Exactly! The damping factor, e^-st, allows the integral to converge for a wider variety of functions. This makes it particularly effective for functions that grow exponentially. That’s essential because many natural phenomena can be modeled this way.

So, that means we can handle functions that a Fourier transform might struggle with?

Yes! The Laplace transform opens doors for analyzing complicated systems in engineering using initial conditions effectively.
Transformation and the s-Domain
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's finish by examining how the transformation into the s-domain helps us. Why do you think working in the s-domain is beneficial?

Because it turns differential equations into algebraic equations?

Exactly! This simplification is crucial for engineers. Can anyone think of practical applications of this in fields like civil engineering or control systems?

In control systems, we can use it to design systems that react correctly to inputs?

Right! Whether in structural dynamics or electrical circuits, the s-domain gives us an easier path to analyze system performance. Keep in mind the acronym LIFT we discussed earlier, as it encapsulates the essence of transforming our functions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section defines the Laplace transform, which converts time-domain functions into s-domain representations. It highlights its significance in engineering, particularly for functions defined for non-negative time and its utility in overcoming the limitations faced by Fourier transforms.
Detailed
Defining the Laplace Transform
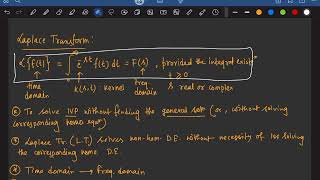
The Laplace transform is a mathematical operation that changes a time-domain function, f(t), defined for t ≥ 0, into a complex frequency-domain function, F(s). It is given by the integral:
$$
F(s) = L\{f(t)\} = \int_{0}^{\infty} e^{-st} f(t) dt
$$
where s is a complex variable defined as s = σ + iω. This transformation allows for the simplification of differential equations, particularly initial value problems, by transforming them into algebraic equations in the s-domain.
The Laplace transform is particularly valuable because it handles functions that are not absolutely integrable over the entire real line, can work with discontinuous and exponentially growing functions, and provides easier methods for dealing with initial conditions. This generalization of the Fourier transform allows engineers and mathematicians to effectively analyze transient behaviors in systems, making it a critical tool in engineering mathematics.
Youtube Videos






![Inverse Laplace transformation Lec-14 First shifting property L^-1[(s+8)/(s^2+4s+16)]](https://img.youtube.com/vi/ii_R0s_dKxo/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Laplace Transform
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let f(t) be defined for t≥0. The Laplace transform is:
Z ∞
F(s)=L{f(t)}= e−stf(t)dt
0
Where s is a complex number: s=σ+iω.
Detailed Explanation
The Laplace transform takes a function f(t) defined for non-negative values of t (t≥0) and transforms it into another function F(s). This is defined mathematically by an integral from 0 to infinity of the product of the original function f(t) and an exponential decay term e^(-st). Here, 's' represents a complex number composed of a real part (σ) and an imaginary part (ω). The factor e^(-st) acts as a damping function, which helps in ensuring convergence of the transform, meaning the integral will yield a finite result.
Examples & Analogies
Imagine you are monitoring the temperature of a soup as it cools down over time. The temperature can be thought of as f(t). The Laplace transform helps you analyze how the temperature decreases over time (due to the cooling) by integrating this over the time it takes for the soup to cool. The 's' in the transform acts like a control knob, allowing you to adjust sensitivity to how quickly the temperature changes.
Generalization of Fourier Transform
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Laplace transform can be seen as a generalization of the Fourier transform by replacing iω with a complex variable s.
Detailed Explanation
The Fourier transform is a specific case of the Laplace transform where the complex variable 's' is replaced with 'iω', where 'i' is the imaginary unit and 'ω' represents angular frequency. This means that while the Fourier transform focuses solely on oscillations and frequency components (using purely imaginary inputs), the Laplace transform allows for more general inputs that can include exponential growth or decay as well, accommodating a wider variety of functions.
Examples & Analogies
Think of the Fourier Transform like a radio tuner that only picks up specific frequencies—like only listening to music on specific stations. The Laplace Transform is like a universal remote that allows you to control not just what music plays, but also how loud it is (damped) or even if it's playing in rewind. This flexibility lets engineers use the Laplace Transform for many more types of signals and systems.
Key Concepts
-
Laplace Transform: An integral transform that converts functions for easier analysis.
-
Damping Factor: The e^{-st} term improves convergence of the integral.
-
Initial Value Problems: Essential for problems that depend on initial conditions in engineering.
Examples & Applications
Transforming the function f(t) = e^{2t} using the Laplace transform gives F(s) = 1 / (s - 2).
For a step function u(t - a), its Laplace transform can be computed and used to analyze delayed responses in systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Laplace transform takes a function and makes it whole, from time to s, that’s its role.
Stories
Imagine a car moving where time stops. With Laplace, we can see what happens as it zips and hops!
Memory Tools
Remember 'DIET' - Damping, Integral, Easy Transformation, helps you see its uses!
Acronyms
Use 'LIFT' for Laplace Integral for Function Transformation, reminding you of the power to raise function analysis.
Flash Cards
Glossary
- Laplace Transform
An integral transform that converts a time-domain function into a complex frequency-domain function, facilitating the analysis of dynamic systems.
- Damping Factor
The term e^{-st} in the Laplace transform that reduces the influence of higher frequencies to improve convergence.
- Initial Value Problem
A type of problem where the solution to a differential equation is determined by initial conditions.
- Complex Variable
A variable that can take on complex numbers, typically expressed as s = σ + iω.
Reference links
Supplementary resources to enhance your learning experience.
