Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Angular Deformations
Unlock Audio Lesson
Today we're going to explore angular deformations in fluid elements. Imagine we have a fluid flow between two parallel plates, one at rest and the other moving. Can anyone tell me what this setup demonstrates?
It shows how the fluid adapts to the motion of the moving plate!
Exactly! This leads to variations in the velocity of fluid particles. We study these to understand how angular deformations begin to happen. Who can describe what happens to a fluid element when it is sheared?
The fluid element gets deformed, causing angles of deformation at its corners.
Great! Let's remember the acronym F.A.C.E for Fluid Angular Changes: Fluid adapts, Angles shift, Can deform, and Experiences stress.
I see how every aspect relates to the concept of deformation!
That's the spirit! In fluids, we have to consider the angle θ that changes as the fluid deforms.
So how do we measure these changes over time?
Good question! Measuring the rate of these changes gives us insight into the angular velocity, which directly relates to the shear strain rate.
To summarize, angular deformations in fluids are driven by shear stress, leading to changes in velocity and angles. Remember, F.A.C.E is your key to recalling this process!
Shear Stress and Shear Strain Rate
Unlock Audio Lesson
Now, let’s dive deeper into how shear stress relates to shear strain rate. Who can define shear stress in fluids?
Shear stress is the force applied per unit area on the fluid.
Correct! Now, how does that relate to strain in fluids versus solids?
In fluids, shear stress relates to the rate of deformation rather than total deformation.
Exactly! We can express this with Newton's law of viscosity, where shear stress is proportional to shear strain rate. Can anyone give me the general formula?
It’s τ = μ * (du/dy), where τ is shear stress and μ is the viscosity coefficient.
Perfect! And why is viscosity crucial in this context?
It indicates how resistant a fluid is to flow and deformation.
Exactly! Viscosity helps us predict how the fluid behaves under different shear rates. Let's not forget, shear rate and viscosity dictate fluid motion.
To wrap up, we've established that shear stress in fluids is not about total deformation but rather about how rapidly they deform.
Influence of Temperature on Viscosity
Unlock Audio Lesson
Now let's talk about the role of temperature. How does temperature impact fluid viscosity?
Higher temperatures usually decrease viscosity in liquids, right?
Correct! Increased temperature leads to more molecular movement, which weakens intermolecular forces. Can anyone compare this to gases?
For gases, higher temperatures actually increase viscosity because of increased molecular collisions.
Well said! So how does this temperature influence translate to practical applications?
In industrial processes, we have to control temperatures to manage viscosity, especially in systems like lubrication!
Absolutely! Managing viscosity can improve efficiency and safety during fluid transport. Alright, so key takeaway: Temperature has a polarizing effect on viscosity between liquids and gases.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains how angular deformations occur in fluid elements when subjected to shear stress due to velocity variations, highlighting the key differences between fluid mechanics and solid mechanics regarding stress relationships and behaviors.
Detailed
Angular Deformations
In fluid mechanics, particularly when examining flow between parallel plates, one plate remains stationary while the other moves with velocity V. This scenario illustrates the concept of angular deformation in a fluid element, where velocity varies linearly from the stationary plate to the moving plate, obeying the no-slip condition. As fluid particles move, they experience angular deformations as they deform over time, transitioning from an original shape to a new configuration represented by different angular positions and angles of deformation.
The section further explains that the rate of change of angular deformation is proportional to the velocity gradient along the flow, establishing a link to the shear strain rate and emphasizing that in fluids, shear stress is proportional to shear strain rate, diverging from solid mechanics where stress relates to total strain values. This forms the basis of Newton's law of viscosity, which defines shear stress with respect to the velocity gradient, showcasing fluid behavior under various conditions. It also discusses the influence of temperature on viscosity and how this impacts fluid properties significantly. The key takeaway is the fundamental difference in stress-strain relationships between fluids and solids and the consequent applications in understanding fluid behavior under motion.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fluid Element and Initial Velocity Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
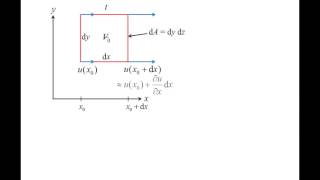
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress. Here what we consider that fluid element. That means, I consider some space of A, B, C, D, this is what the fluid element.
Detailed Explanation
This chunk introduces the concept of fluid flow between two parallel plates. One plate is stationary while the other moves with a certain velocity (V). At the position of the no-slip condition, the fluid adjacent to the stationary plate has zero velocity, while the fluid closest to the moving plate has velocity V. The fluid is considered as a 'fluid element' defined by points A, B, C, and D, which allows for a clearer analysis of how velocity varies within the fluid layer.
Examples & Analogies
Think of this scenario as a two-lane highway where one lane is blocked (stationary) and the other is flowing smoothly (moving). The cars (fluid particles) closest to the congested lane (stationary plate) hardly move, while those closer to the free lane (moving plate) can accelerate up to the speed limit (velocity V).
Linear Velocity Variation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it that at the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A.
Detailed Explanation
In this section, we discuss the concept of linear velocity distribution within the fluid element. Given that point A is closest to the moving plate with velocity V while point B is adjacent to the stationary plate with a velocity of zero, we can infer that the velocity changes uniformly from point B to point A. This results in a linear gradient of velocities, an important concept when analyzing shear stress in fluid mechanics.
Examples & Analogies
Imagine a water slide—at the top (point A), the water flows quickly, while at the bottom (point B), it slows down as it interacts with the ground. This gradual change in speed creates a 'ramp' of speed that allows the riders to experience a smooth descent rather than a sudden drop.
Angular Deformations Over Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
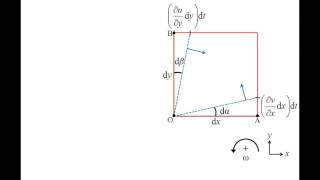
After ∆t time these fluid element will be deformed as a angular deformations will happen it that there will be angle θ will come it at the B and E, F and D. That is a new positions of the fluid element after ∆t time.
Detailed Explanation
After a small amount of time ∆t, the fluid element will undergo a deformation due to the velocity gradient that exists between the two plates. This deformation results in angular displacements (θ) at points B, E, F, and D, showing how the originally rectangular shape of the fluid element is altered as fluid layers slide past one another. This concept is crucial to understanding how materials respond to shear forces.
Examples & Analogies
Picture stretching a slinky: as you pull one end away from the other, the coils begin to lean and create angles rather than remaining neatly organized. This represents how a fluid element adjusts to external forces, changing shape over time in the flow.
Rate of Change of Angular Deformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At the ∆t time we have angular deformations of θ. Consider a very simple geometry of these problems. I can consider these distance of AE is V into delta t divide by l will be the 10 θ since θ is very small.
Detailed Explanation
Here, we derive a relationship that relates the changes in deformation to time and geometry. We consider the distance between points A and E (where the angular deformations occur) to calculate how much the angle θ changes over the time interval ∆t. The assumption that θ is small allows us to use small angle approximations which simplify calculations of angular deformations in fluid mechanics.
Examples & Analogies
Think of pushing a door open. If you push it slightly (like a small angle), you can easily predict how much more it will open based on how long you push it—much like calculating the angle change in a fluid element.
Shear Stress and Shear Strain Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear strain rate and the velocity gradient is equal for these conditions.
Detailed Explanation
In the context of fluid flow between parallel plates, we find that the shear strain rate is directly proportional to the velocity gradient. This means that how fast the fluid layers slide past one another (shear rate) is directly related to the difference in velocities over distance. This relationship is foundational in fluid mechanics as it describes how fluids behave under shear forces.
Examples & Analogies
Imagine spreading butter on bread. The faster you glide the knife over the surface, the more 'shear' you are applying to the butter. As the speed increases, the layer of butter deforms more—reflecting how shear stress functions in a fluid.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear stress is a proportionality to the shear strain rate and that is the Newton's laws of viscosity that shear strain is a proportionality to the shear strain rate.
Detailed Explanation
This chunk introduces Newton's law of viscosity, which states that the shear stress in a fluid is directly proportional to the shear strain rate. This relationship illustrates that as the fluid's layers move faster relative to each other, the resulting shear stress increases. This law is essential for understanding fluid dynamics and is often used in engineering applications to calculate the behavior of fluids under various conditions.
Examples & Analogies
Think of honey. If you apply a gentle force (shear stress), it flows easily (shear strain), but if you try to push it harder (more shear stress), it resists more. This resistance is what Newton’s law of viscosity helps describe.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Stress: A force exerted on a fluid causing it to deform.
-
Viscosity: The resistance of a fluid to flow and deformation.
-
Angular Deformation: The alteration of angles in a fluid element due to shear stress.
-
Shear Strain Rate: The change in shear deformation with time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When honey flows off a spoon, its high viscosity slows down the process compared to water, demonstrating how fluid resistance differs.
-
Toothpaste behaves as a Bingham plastic; it requires a certain force to start flowing before it deforms willingly.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Shear stresses flow and angles change, in fluids, this behavior isn't strange.
📖 Fascinating Stories
-
Once there was a plate at rest and one on the go, fluid flows between, oh, what a show! The fluid starts to twist and turn, angular deformation is what we learn.
🧠 Other Memory Gems
-
Use the acronym S.V.A.S: Shear stress, Viscosity, Angular deformation, Shear strain rate.
🎯 Super Acronyms
Remember **F.A.C.E** for Fluid Angular Changes
- Fluid adapts
- Angles shift
- Can deform
- Experiences stress.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
The stress component parallel to a given plane in a material, resulting from forces acting tangential to the specified surface.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow or deformation, represented by the proportionality constant in shear stress equations.
-
Term: Angular Deformation
Definition:
The change in angle of a fluid element under shear stress, indicative of its deformation during flow.
-
Term: Shear Strain Rate
Definition:
The rate at which shear deformation occurs in a fluid, with respect to time.