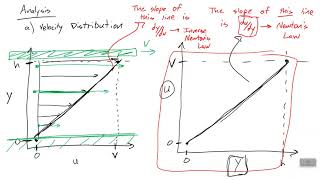
Velocity Variation from B to A
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Fluid Velocity Profile
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the concept of fluid velocity in a scenario where one plate is stationary while the other moves. Why do you think we get a velocity of zero at the stationary plate?

Because the fluid sticks to the plate and doesn't move!

Exactly! That's the no-slip condition. As we move away from that plate, how do we expect the velocity to change?

It should increase linearly until it reaches the velocity of the moving plate, V.

Correct! We describe this increase as a linear velocity profile from zero at the stationary plate to V at the moving plate. Let's think of it like a ramp where velocity gradually rises as we move upwards.

So, if I take a point 'y' away from the stationary plate, how would I calculate the fluid velocity at that point?

You would use the relationship between y and V to evaluate the velocity V_y = (V/l) * y, where l is the distance between the plates. This reinforces our understanding of linear variation.

It's interesting how we can visualize this with a linear graph!

Yes! To summarize, the velocity varies linearly between the two plates from zero to V, a foundational concept in fluid mechanics.
Shear Stress and Viscosity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's dive into shear stress. How is shear stress defined in fluids?

Isn't it related to how fast the fluid layers are sliding past each other?

Absolutely! Shear stress is proportional to the rate of change of velocity, known as the velocity gradient. This relationship is crucial in understanding fluid behavior. What can you tell me about Newtonian fluids?

In Newtonian fluids, the viscosity is constant regardless of the shear rate!

Exactly! And how does this differ from non-Newtonian fluids?

Non-Newtonian fluids have a viscosity that changes with the shear rate.

Right! This distinction impacts how we model fluid flows in various applications. Remember, the relationship we often use is described by the equation τ = μ * (du/dy), where τ is shear stress, μ is viscosity, and du/dy is the velocity gradient.

So shear stress is related to how quickly the fluid layers move past each other, which is essential for understanding fluid mechanics!

Well summarized! This relationship forms the foundation of many fluid dynamics equations.
Temperature and Viscosity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's discuss how temperature impacts viscosity. What happens to the viscosity of liquids as temperature increases?

I think it decreases because the molecules can move more freely!

That's right! Increased temperature enhances the kinetic energy of molecules, thus reducing intermolecular interactions and leading to lower viscosity. How does this compare with gases?

For gases, the viscosity actually increases with temperature because the molecules move more and collide more often, right?

Exactly! This difference is crucial when studying how fluids behave under various conditions. Increased motion in gases leads to more viscosity, while it decreases in liquids. Now, can anyone summarize why understanding these concepts is essential?

It helps predict how fluids will behave in different situations, which is important for engineering applications!

Well said! Fluid dynamics is about understanding these fundamental relationships to design and analyze systems effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we analyze the behavior of fluid velocity in a parallel plate flow scenario where one plate is stationary and the other moves with a velocity V. We discuss the significance of no-slip conditions, the concept of shear stress proportional to the velocity gradient, and the distinction between Newtonian and non-Newtonian fluids. The effects of temperature on viscosity and its correlation with molecular motion are also highlighted.
Detailed
Velocity Variation from B to A
In this section, we delve into the velocity profile of a fluid flowing between two parallel plates. One plate remains stationary (velocity = 0), while the other moves with a velocity V, resulting in a linear variation of fluid velocity between the two plates. This phenomenon follows the no-slip condition at the boundaries, where fluid in contact with the stationary plate has zero velocity. As we move away from the stationary plate towards the moving plate, the fluid velocity increases linearly from zero to V.
Key concepts discussed include the calculation of velocity at distances from the plates, the definition of shear stress as a function of the velocity gradient, and how these concepts connect to shear strain rates. We introduce the principle that shear stress is proportional to the rate of change of deformation, distinguishing the behavior of Newtonian fluids (where viscosity remains constant) from non-Newtonian fluids (where viscosity varies with shear rate).
The role of temperature in affecting viscosity is explored, emphasizing how increased temperatures enhance molecular motion in liquids, thus decreasing viscosity, while also noting that pressure changes do not significantly impact viscosity in many cases. The section concludes with an overview of the fundamental equation for shear stress in terms of viscosity and shear strain rate, linking these macroscopic observations back to the underlying molecular dynamics.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fluid Flow Through Parallel Plates
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If I consider the same fluid flow through a parallel plate, okay. One of the plates has a velocity of zero at rest conditions and the other top plate is moving with a velocity V.
Detailed Explanation
In this situation, we analyze a fluid flowing between two parallel plates. One plate is stationary (velocity = 0), while the other is moving at a constant speed V. This setup is crucial for understanding how fluids behave under shear stress, particularly in scenarios such as lubrication and flow in pipes.
Examples & Analogies
Imagine a slice of bread with a layer of jelly on it. If you push the top slice (the moving plate), the jelly (the fluid) will be disturbed. The bread below this jelly represents the stationary plate. The jelly closest to the top slice moves faster than the jelly closest to the bread.
Velocity Distribution from B to A
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As a microscopic point of view, we consider the fluid element defined by points A, B, C, D. The velocity at A is V due to no-slip conditions, and at B, it is 0. Thus, there is a linear velocity variation from B to A.
Detailed Explanation
In fluid mechanics, 'no-slip condition' means that fluid at a boundary (the surface of the plate) has the same velocity as the boundary. Here, point A has velocity V since this plate is moving, while point B has zero velocity as it is at rest. The fluid's velocity between these two points varies linearly, indicating that as we move from the resting plate to the moving plate, the velocity increases proportionally from 0 to V.
Examples & Analogies
Think of pushing a child on a swing. Near the base where the swing is attached (the resting plate), the child is still (velocity = 0), but as you push and they swing higher away from the attachment point (the moving plate), they gain speed (velocity increases).
Angular Deformations Over Time
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
After a time interval, the fluid element will be deformed into new positions, leading to angular deformations at certain points.
Detailed Explanation
Fluid elements are not just moving; they reshape themselves due to shear forces acting on them. Over time, as the moving plate continues, the arrangement and alignment of the fluid particles change. This results in angular deformation, where the original rectangular shape of the fluid can change to a parallelogram shape because of the velocity differences, especially close to the moving plate.
Examples & Analogies
Visualize stretching a piece of dough while making pizza. If you apply pressure to the dough, it doesn’t just elongate. It also gets thinner in some areas and changes its original shape. Similarly, the fluid element deforms over time under shear stress.
Rate of Change of Angular Deformations
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The rate of change of angular deformations in this fluid element can be analyzed to understand shear strain rate.
Detailed Explanation
The angular deformation of the fluid can be quantified by observing how drastically the shape of the fluid element changes over a brief period. This analysis gives insights into the shear strain, which describes how much the shape of the fluid changes due to applied forces. The shear rate is directly linked to the fluid's viscosity and can determine how much the fluid resists deformation.
Examples & Analogies
Consider a rubber band. When you pull it, it stretches, and the rate at which it stretches depends on how much force you're applying. The faster you pull it (higher shear rate), the more it deforms (higher strain). Similarly, fluids react based on the forces acting on them.
Shear Stress and Velocity Gradient Relationship
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In parallel flow conditions where the velocity has a linear distribution, the shear strain rate and the velocity gradient are equal.
Detailed Explanation
Shear stress in fluids is directly proportional to the velocity gradient. When you have a straightforward linear relationship between the speed of the fluid and the distance from the stationary surface, you can observe that the rate of change of velocity per distance (velocity gradient) corresponds to the shear applied. This relationship is fundamental in fluid mechanics.
Examples & Analogies
Think of a conga line. The first person (at the front) moves faster, and as you go further back in line, each person moves at slightly slower speeds. The rate of change of speed from the first person to the last directly correlates to how fast everyone else can move, similar to how shear stress works in fluids.
Difference Between Fluid and Solid Mechanics
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, the stress is proportional to the shear strain rate, while in solid mechanics, it is related to the absolute shear strain.
Detailed Explanation
This distinction highlights how fluids behave differently compared to solids. In fluids, the stress and strain rates are linked dynamically; the stress responds to the rate at which deformation occurs rather than the total deformation itself, unlike solid materials that respond to the total shape change. This is a key principle underpinning the study of fluid flow and dynamics.
Examples & Analogies
Imagine a sponge soaking up water. The sponge can compress (deform) without resistance when you squeeze it. If you squeeze harder (higher shear strain rate), it resists more than when you are simply applying force without quickly changing its shape.
Newton's Law of Viscosity
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The shear stress is proportional to the shear strain rate, which leads to the definition of viscosity as a proportionality constant.
Detailed Explanation
Newton's law of viscosity states that the shear stress is directly proportional to the shear strain rate, represented mathematically as shear stress = viscosity × shear strain rate. This definition allows for a quantifiable measure of how a fluid deforms under shear stress, which is crucial for practical applications in engineering and physics.
Examples & Analogies
Think of oil in a frying pan. When the pan is on heat and you stir the oil, the oil flows easily (less viscous) compared to honey, which flows much more slowly (more viscous). This demonstrates how viscosity affects the flow of fluids.
Key Concepts
-
No-slip condition: The velocity of fluid at the boundary of a surface is zero.
-
Shear Stress: A measure of how much force per unit area is applied to a fluid.
-
Viscosity: A material property that represents a fluid's resistance to deformation.
-
Newtonian Fluids: Fluids with constant viscosity across shear rates.
-
Non-Newtonian Fluids: Fluids whose viscosity changes depending on the shear rate.
Examples & Applications
A fluid flowing between two plates demonstrates linear velocity variation, crucial for understanding viscous flow.
Temperature can influence the viscosity of liquids, as observed when heating syrup, making it flow more easily.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In fluids that flow, stress and strain, shear's the name, viscosity's the game!
Stories
Picture a river with a boulder. The water moves slowly next to it, not daring to flow past. Further out, the water moves swiftly. This represents the layers of fluid, showing us the no-slip condition!
Memory Tools
V-NV (V for Viscosity, NV for Non-Newtonian) to remember that Newtonian's viscosity is stable, while Non-Newtonian's is not!
Acronyms
S.V.V. - 'Stress, Velocity, Viscosity.' Think about how these factors relate in fluid dynamics!
Flash Cards
Glossary
- Noslip condition
The assumption that fluid in contact with a surface has zero velocity relative to that surface.
- Shear Stress
The force per unit area exerted by fluid layers sliding past one another.
- Viscosity
A measure of a fluid's resistance to flow or deformation.
- Newtonian Fluid
A fluid where viscosity remains constant regardless of the shear rate.
- NonNewtonian Fluid
Fluids whose viscosity changes with the shear rate.
Reference links
Supplementary resources to enhance your learning experience.
