Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Fluid Flow and Shear Stress
Unlock Audio Lesson
Today, we'll discuss fluid flow through parallel plates and how shear stress is established. When one plate is stationary and the other moves, the fluid layers experience different velocities.
What exactly is shear stress, though?
Excellent question! Shear stress is essentially the force per unit area that acts parallel to the surface of the fluid. It's caused by the friction between moving layers of fluid.
So, if I understood correctly, shear stress helps us understand how fluids resist flow?
Exactly! Shear stress relates directly to how the velocity of fluid layers changes with distance. This relationship helps us quantify the viscosity of the fluid.
Is there a formula we can use to calculate this?
Yes, we can relate it through the Newton's law of viscosity, where shear stress = viscosity × shear strain rate. Remembering this relationship is crucial!
Just to recap, the shear strain rate is the change in velocity across the fluid layer, right?
Correct! Great job everyone. To sum up, shear stress arises from the fluid's movement, and its relationship with strain rate allows us to understand fluid viscosity.
Effects of Temperature and Pressure on Viscosity
Unlock Audio Lesson
Now, let's explore how temperature and pressure influence viscosity. Who can explain what happens to viscosity as temperature changes?
I think increasing temperature usually decreases viscosity in liquids, right?
Absolutely! When we increase temperature, the molecular motion enhances, reducing intermolecular forces. This is why liquids become 'thinner' at higher temperatures.
How about gases? Do they react similarly?
Good point! In contrast, for gases, as temperature increases, viscosity tends to increase. The increased motion leads to more collisions and, therefore, higher resistance to flow.
And what about pressure? Does that affect viscosity much?
Generally, pressure has minimal effects on liquid viscosity, typically resulting in less than a 0.5% change when moving from atmospheric pressure to high pressures.
So pressure doesn’t really change the way molecules interact much for liquids?
Exactly! Keep in mind these principles help us in applications like fluid transport in pipelines. To wrap up, temperature affects viscosity differently for liquids and gases, while pressure has a negligible effect on liquids.
Newtonian vs. Non-Newtonian Fluids
Unlock Audio Lesson
Let's differentiate Newtonian fluids from non-Newtonian fluids. Who remembers what characterizes a Newtonian fluid?
Is it that the shear stress is directly proportional to the shear strain rate?
Correct! Newtonian fluids have a constant viscosity regardless of the shear rate, which simplifies calculations.
What about non-Newtonian fluids? What makes them different?
Non-Newtonian fluids do not follow a linear relationship between shear stress and shear strain. Their behavior can change based on the shear rate, which we categorize into types such as pseudoplastic and dilatant fluids.
Can you give an example of each?
Certainly! Toothpaste is a classic example of a dilatant fluid, where higher shear forces are required at higher deformation rates. Conversely, paints are often pseudoplastic fluids, thinning as they are stirred.
So we see that viscosity can be complex depending on the fluid!
Absolutely, understanding these differences is essential for practical applications in various fields. Remember, Newtonian materials have consistent viscosity, while non-Newtonians vary in response to shear.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of viscosity is examined through the interaction of fluid layers between stationary and moving plates. The relationship between shear stress and strain rate is discussed, alongside how temperature and pressure affect viscosity in liquids and gases, demonstrating the differences in behavior between Newtonian and non-Newtonian fluids.
Detailed
Molecular Levels and Viscosity
This section delves into fluid dynamics by considering the flow of a fluid between two parallel plates—one at rest and one in motion. The concept of viscosity is introduced through the analysis of shear stress and strain rate, where shear stress is proportional to the rate of deformation of the fluid. Key distinctions are made between solids and fluids in terms of how stress relates to strain; whereas in solids, stress is proportional to strain, in fluids, stress is proportional to shear strain rate.
The section goes on to illustrate how molecular dynamics play a crucial role in determining the viscosity of liquids and gases. It highlights the influence of temperature and pressure on viscosity, particularly noting that while pressure has little effect on liquid viscosity, temperature significantly alters molecular movement—a rise in temperature decreases viscosity in liquids and increases it in gases. This fundamental understanding underpins the differentiation between Newtonian fluids, which obey the linear proportionality of shear stress to shear strain rate, and non-Newtonian fluids, which display more complex behaviors under varying deformation rates.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fluid Element Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider the same fluid flow through a parallel plate, okay. One of the plate velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting in a shear stress. Here what we consider that fluid element.
Detailed Explanation
This chunk discusses the basic setup of fluid dynamics in a parallel plate scenario where one plate is stationary and the other is moving. In this context, viscosity is understood by examining how fluid elements behave due to the movement. The zero velocity of one plate demonstrates the no-slip condition, where fluid adheres to the surface. The top plate’s movement generates a velocity gradient within the fluid, which is crucial for analyzing shear stress, although the chunk does not delve into the molecular motions.
Examples & Analogies
Consider moving your hand through water. While your hand moves through the water with some speed (analogous to the moving plate), the water directly in contact with your hand does not move (like the stationary plate). The water just below it starts to move slightly, creating a flow, similar to what is described with the fluid element between the plates.
Velocity Gradient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it that at the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A. That linear velocity from zero to V as the y increases, the velocity will increase it and maximum velocity will be the V.
Detailed Explanation
This chunk elaborates on the velocity gradient between the two plates. The no-slip condition means that at the surface of the stationary plate (point B), the fluid has zero velocity, while at the moving plate (point A), the fluid reaches its maximum velocity V. This creates a linear gradient across the gap between the plates, effectively demonstrating how velocity changes with distance. The key point here is that the change in velocity is not uniform but varies linearly according to the distance from the stationary plate.
Examples & Analogies
Think of a slide at a playground. At the top (the no-slip condition), you’re not moving at all, but as you slide down, you accelerate. Similarly, in the fluid layer next to the stationary plate, the fluid does not move, but as you move away from it towards the moving plate, you gain speed until you reach maximum velocity.
Angular Deformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After ∆t time these fluid element will be deformed as angular deformations will happen it that there will be angle θ will come it at the B and E, F and D.
Detailed Explanation
This chunk introduces the concept of angular deformations that occur in the fluid element over time due to the velocity gradients. As the fluid moves, it experiences shear, causing it to change shape and form angles between different points of the fluid element. This deformation helps in understanding the relationship between stress and strain in fluid systems, showing that even without rigid boundaries, fluids can experience internal changes.
Examples & Analogies
Imagine a soft sponge: when you press it down, it shifts and changes shape rather than just moving as a solid block. Similarly, as the fluid element between the plates flows, the layers can shift relative sideways, creating angular deformations as they respond to the differences in velocities.
Shear Stress and Strain Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Shear strain rate is equal to the velocity gradient, which indicates how much the fluid layers move relative to each other. The shear stress is proportional to this strain rate, which is aligned with Newton's laws of viscosity.
Detailed Explanation
Here, the relationship between shear stress and shear strain rate is defined. As the fluid flows and experiences shear, there is a direct proportionality between the rate of deformation (shear strain rate) and the resulting shear stress. According to Newton’s laws of viscosity, this means the greater the velocity gradient, the greater the shear stress experienced by the fluid, affirming the concept of viscosity as a resistance to flow.
Examples & Analogies
Think about squeezing honey from a bottle. The harder you squeeze (increasing the shear stress), the more honey flows out, which corresponds to an increase in shear strain rate. This is similar to how fluid elements respond under shear stress: they flow progressively more as shear stress increases.
Effect of Temperature on Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us commit that how how does the temperature effect on the coefficient of the viscosity. Now we have to look at the molecular levels okay. So if you look at this molecular levels, when you talk about the liquids, they will have a molecular bonding forces between two molecules okay. But that is much weaker when talk about the gases.
Detailed Explanation
This chunk begins to discuss how temperature influences viscosity at a molecular level. In liquids, molecules are held together by stronger bonding forces compared to gases, where molecules are more loosely arranged and move in a more random motion. As temperature increases, these molecular bonds weaken in liquids, ultimately leading to a decrease in viscosity. This is significant as the ability of fluids to flow changes with temperature, impacting practical applications in various fields.
Examples & Analogies
Think of melting butter. When it's solid, it doesn't flow (high viscosity), but as it heats up, it turns to liquid and flows easily (low viscosity). As temperature increases, similar changes occur in liquids regarding their viscosity, showcasing how temperature affects flow.
Differences Between Liquids and Gases
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the temperatures, the temperatures related is that how much of collisions are happening. For liquids, let us look it that change of the pressures will not change that significantly through coefficients of viscosity which represent as a proportionality constant of mass exchange of the molecules or momentum exchange of molecules from one layer to other layers.
Detailed Explanation
This segment highlights the fundamental differences in how liquids and gases respond to changes in temperature and pressure concerning their viscosity. It emphasizes that while an increase in pressure has minimal effect on the viscosity of a liquid, temperature plays a major role by increasing molecular collisions, resulting in significant changes in viscosity as temperature rises.
Examples & Analogies
Imagine heating a pot of water versus a balloon filled with air. The water (liquid) becomes less viscous and flows better as heat is added, while the air (gas) becomes more energetic but its viscosity remains relatively constant. This illustrates how different states of matter react differently under the same conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Stress: The force acting parallel to the fluid layers resulting from their relative motion.
-
Viscosity: The internal friction in a fluid that determines its resistance to flow.
-
Newtonian Fluids: Fluids with constant viscosity independent of applied shear rates.
-
Non-Newtonian Fluids: Fluids whose viscosity varies with shear rates, displaying complex behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Toothpaste exhibits dilatant behavior, requiring more force to flow as pressure is applied.
-
Paints often behave as pseudoplastic fluids, thinning under shear like stirring.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids that flow without a fight, shear stress must be parallel, that's right!
📖 Fascinating Stories
-
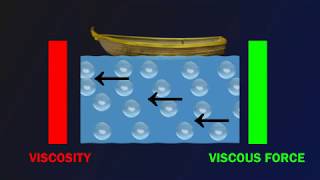
Imagine a calm pond with a small boat. As the boat moves, it drags water behind it, creating waves—the water layers experience shear stress as they glide past each other.
🧠 Other Memory Gems
-
To remember Newtonian: 'N for Not changing, V for Viscosity remains.'
🎯 Super Acronyms
VIE
- Viscosity
- Internal friction
- Elasticity - key to fluid behavior!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
The force per unit area acting parallel to the layers of fluid, caused by the friction between moving layers.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow, representing the internal friction within the fluid.
-
Term: Newtonian Fluid
Definition:
A type of fluid whose viscosity remains constant regardless of the shear rates applied.
-
Term: NonNewtonian Fluid
Definition:
Fluids whose viscosity changes significantly with varying shear rates.
-
Term: Shear Strain Rate
Definition:
The rate at which the velocity of fluid layers changes with distance, affecting how the fluid flows.