Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Basics of Fluid Flow
Unlock Audio Lesson
Today, we will discuss how fluids behave when they flow between two parallel plates, which is called shear flow. Can anyone explain what happens to the velocity of the fluid between these plates?
The fluid velocity increases from one plate to the other.
Exactly! So if one plate is moving at velocity V and the other is stationary, we see a linear velocity distribution. As you move away from the stationary plate, the velocity gradually increases. This is essential for understanding shear strain rate. Let's remember: V = Velocity at the moving plate.
So, the shear strain rate relates to how fast this velocity changes across the fluid?
Absolutely! This change in velocity across a specific distance is what we call the velocity gradient. Keep this in mind as it lays the groundwork for our next topic!
Defining Shear Strain Rate
Unlock Audio Lesson
Now, let us delve into the shear strain rate. Who can summarize what shear strain rate means in the context of fluid flow?
I think it's the change in shape of the fluid element over time due to shear stress.
That's correct! Mathematically, we express shear stress as proportional to shear strain rate. This relationship can be expressed using Newton's law of viscosity: shear stress = mu * shear strain rate. 'Mu' here is the coefficient of viscosity. Can anyone recall what influences the coefficient of viscosity?
Temperature is a factor! Higher temperatures can lower viscosity in liquids.
And what about gases?
Great follow-up! In gases, increasing temperature usually increases viscosity due to increased molecular motion. So, **remember**: viscosity can vary based on the state of the fluid. Let’s encapsulate this: shear rate = shear stress/mu.
Differentiating Fluid and Solid Mechanics
Unlock Audio Lesson
As we explore shear strain and stress, it's important to highlight the differences between fluid mechanics and solid mechanics.
Is it about stress and strain relations?
Exactly! In solid mechanics, stress is proportional to strain. However, in fluid mechanics, stress is proportional to strain rate. This is significant! Can anyone help me summarize why this is essential?
It shows how fluids respond differently compared to solids under force.
Spot on! The behavior of fluids involves shear stress and strain rates, providing insight into how fluids flow. Let's keep this in mind as we move forward.
The Role of Temperature and Pressure on Viscosity
Unlock Audio Lesson
Now that we have understood the shear strain rate, let’s discuss how external factors like temperature and pressure impact viscosity.
We talked about how temperature affects liquids, but can pressure also influence viscosity?
Correct! While pressure changes typically have minimal effect on viscosity, temperature changes can significantly influence it—liquids experience a decrease in viscosity as temperature rises. Can anyone think of a scenario where this is applicable?
Cooking oil viscosity decreases when heated on the stove!
Excellent example! So remember, temperature can dramatically alter viscosity, especially in liquids. Now let’s summarize our learnings today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the shear strain rate relation in fluids flowing between parallel plates, examining how velocity gradients produce shear stress. It highlights the distinction between fluid mechanics and solid mechanics, particularly how shear stress is proportional to shear strain rate in fluids as defined by Newton's laws of viscosity.
Detailed
Shear Strain Rate Relation
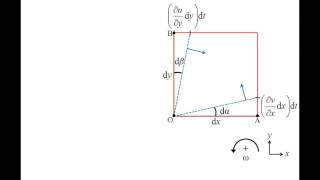
This section delves into the essential concepts of shear strain rate relation in fluid mechanics, particularly how it applies to fluids flowing between two parallel plates. In this scenario, one plate is stationary while the other moves at a velocity V, creating a velocity gradient across the fluid. Key points include:
- Velocity Distribution: The velocity varies linearly from zero at the stationary plate to V at the moving plate, creating a velocity gradient.
- Angular Deformations: Over a small time increment, the fluid element experiences angular deformations that can be quantified.
- Shear Strain Rate: The relationship between shear strain rate and the velocity gradient is established, which is crucial for understanding Newtonian fluids. This leads to the conclusion that shear stress is proportional to shear strain rate, differing from solid mechanics where stress relates directly to strain.
- Newton's Laws of Viscosity: These laws define the direct relationship between shear stress and shear strain rate in Newtonian fluid behavior, highlighting that the coefficient of viscosity remains constant under varying conditions.
- Effect of Temperature and Pressure: The section briefly touches on how temperature influences viscosity, stating that increased temperatures generally decrease viscosity in liquids but increase it in gases. Additionally, pressure changes have a minimal effect on viscosity.
This section lays the foundational understanding of fluid behavior which will recur in further discussions surrounding different types of fluids and their properties.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Motion Between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
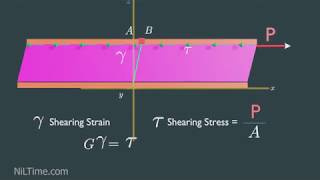
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress.
Detailed Explanation
This passage sets the stage for understanding fluid dynamics between two parallel plates. One plate is stationary (velocity = 0), while the other moves at velocity V. This setup creates a shear stress in the fluid between them due to the difference in motion between the two plates.
Examples & Analogies
Imagine spreading butter on bread. The knife represents the moving top plate, while the bread represents the stationary bottom plate. The butter (fluid) moves along with the knife, and the friction between the knife and the butter creates shear stress.
Velocity Distribution in Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A. That linear velocity from zero to V as the y increases, the velocity will increase it and maximum velocity will be the V.
Detailed Explanation
In this chunk, we explore the velocity profile in the fluid between the two plates. According to the no-slip condition, the fluid at the stationary plate has a velocity of 0, and at the moving plate (A), the fluid travels at velocity V. This creates a linear gradient of velocity throughout the fluid, which means that as we move from the stationary plate to the moving plate, the velocity gradually increases.
Examples & Analogies
Think of a slow-moving escalator. The people at the bottom (the stationary plate) are not moving, while the people at the top (the moving plate) are moving at the speed of the escalator. As you move up the escalator, you gradually gain speed.
Angular Deformation in Fluid Element
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After ∆t time these fluid element will be deformed as a angular deformations will happen it that there will be angle will come it at the B and E, F and D.
Detailed Explanation
During the fluid flow, the fluid elements experience angular deformation over a small time increment (∆t). This means that the shape of the fluid element changes, causing the angles at different points of the element to shift, indicating that the fluid is not rigid and can deform under shear stress.
Examples & Analogies
Imagine stretching a rubber band. When you pull it, it deforms and changes shape. Similarly, the fluid elements deform in response to the movement of plates, which results in angular changes in their shape.
Rate of Change of Angular Deformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At the ∆t time we have a angular deformations of ... . I can consider these distance of AE is V into delta t divide by the l will be the 10 (angle) for since angle is very small, I can consider.
Detailed Explanation
Here, we calculate the rate of change of angular deformation by relating distance (AE), velocity (V), and time (∆t). Since the angle of deformation is small, we can approximate this relationship to understand how quickly the fluid is deforming relative to the distance between the plates.
Examples & Analogies
Think of a pencil being twisted while one end remains still. The degree of twist at the free end is proportional to how hard you twist and how far along the pencil you apply that twist.
Shear Strain Rate to Velocity Gradient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can now consider it that the shear rate strain rate and the velocity gradient is equal for these conditions...
Detailed Explanation
This point clarifies that under linear flow conditions, the shear strain rate (how quickly the shape changes due to shear) is directly related to the velocity gradient (the change in velocity over the distance between the plates). This illustrates a fundamental property of fluid mechanics.
Examples & Analogies
Consider squeezing a sponge. The tighter you squeeze, the more the shape of the sponge deforms, directly related to how hard and how much you push down on it.
Proportionality of Shear Stress and Shear Strain Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are talking about the stress is proportionality to the strain rate. That means the change of the shear strain rate with respect to time, not the absolute value of the shear strain.
Detailed Explanation
In this segment, it distinguishes between the concepts of stress in fluids versus solids. In fluids, shear stress is proportional to the shear strain rate rather than the absolute change in deformation. This highlights how fluids behave differently under stress compared to solid materials.
Examples & Analogies
Think of cooking pasta. When you stir the water (fluid), it starts swirling faster without visibly changing its shape because the motion (strain rate) increases with your stirring effort (stress) without changing the size of the pot.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That is what it happen this shear strain is a proportionality to the shear strain rate. Again I can emphasize to that shear strain rate not the shear strain.
Detailed Explanation
This emphasizes the critical understanding of Newton's law of viscosity which states that shear stress in a fluid is directly proportional to the rate of shear strain, thus establishing a key relationship in fluid mechanics.
Examples & Analogies
Consider a person trying to push a cart on a smooth floor versus a sandy surface. The cart moves easier and faster on smooth floors (low viscosity) compared to sandy surfaces (high viscosity), demonstrating how the resistance (stress) changes with different types of materials (strain rates).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Stress: It is the force applied parallel to the surface area of a material leading to deformation.
-
Shear Strain Rate: It is a measure of how quickly the strain changes in response to the applied shear force.
-
Viscosity: A characteristic property of fluids, indicating their resistance to flow; it varies with temperature and pressure.
-
Newtonian Fluids: These fluids exhibit linear behavior: shear stress directly correlates to shear strain rate.
-
Velocity Gradient: A crucial concept in determining how fast fluid velocity changes in relation to distance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a moving plate causes fluid velocity to increase linearly, it's an example of shear flow.
-
Cooking oil becoming less viscous when heated is an example of temperature affecting viscosity.
-
Syrup has a higher viscosity than water, demonstrating the differences in fluid resistance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Shear stress in action, strain comes in reaction.
📖 Fascinating Stories
-
Imagine a chef whipping cream; the more vigorously they stir, the stiffer the cream gets. That's viscosity reacting to shear!
🧠 Other Memory Gems
-
SST—Shear Stress Leads to Strain; a reminder of how stress impacts strain rates in fluids.
🎯 Super Acronyms
VSL—Viscosity Depends on Shear and Layer, summarizing key factors affecting viscosity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
A force per unit area acting parallel to a surface, caused by fluid motion.
-
Term: Shear Strain Rate
Definition:
The rate at which shear strain occurs in a material, indicating how quickly the deformation takes place.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to deformation or flow, often denoted by the symbol μ.
-
Term: Velocity Gradient
Definition:
The change in velocity of a fluid per unit distance, crucial for determining shear stress.
-
Term: Newtonian Fluid
Definition:
A fluid that follows Newton's laws of viscosity, exhibiting a linear relationship between shear stress and shear strain rate.