Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Shear Stress and Velocity Gradients
Unlock Audio Lesson
Today we're discussing shear stress and how it relates to velocity gradients in Newtonian fluids. Can anyone tell me what shear stress is?
Isn't shear stress the force per unit area that causes the fluid to deform?
Exactly! Shear stress is indeed the force applied over an area. In the context of Newtonian fluids, there's a proportional relationship between shear stress and the velocity gradient. Do you know what a velocity gradient is?
Is it how quickly the fluid's velocity changes from one layer to the next?
Correct! The velocity gradient is a measure of that change. Remember the acronym 'SV' for Shear and Velocity. It helps us remember their connection!
So, if we have a stationary plate and another that moves, the fluid in between layers would change speed?
Exactly! The fluid at the stationary plate has a velocity of zero, while closer to the moving plate it has a higher velocity up to V. This creates that linear gradient.
What happens to the fluid over time?
Great question! Over time, those layers will deform, demonstrating angular deformations at various points. Let’s summarize: shear stress leads to a velocity gradient in Newtonian fluids, which is a linear relationship.
Newton's Law of Viscosity
Unlock Audio Lesson
Now, let's dive into Newton's law of viscosity. Who can tell me what it states?
It states that the shear stress is proportional to the shear strain rate?
Correct! This means that for Newtonian fluids, if we increase the shear strain rate, the shear stress also increases proportionally. Make sure to remember 'SS = μ × SG', where SS is Shear Stress, μ is viscosity, and SG is Shear Gradient.
Does that mean viscosity doesn’t change with different rates?
Exactly! For Newtonian fluids, viscosity remains constant regardless of the rate of deformation. That’s a defining characteristic!
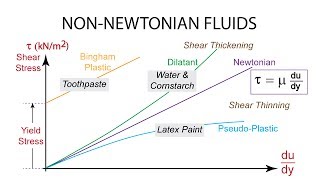
And what about non-Newtonian fluids?
Non-Newtonian fluids do not follow this rule. Their viscosity can change based on the shear rate. This leads us into our next discussion!
Temperature and Viscosity Relationship
Unlock Audio Lesson
Now let’s discuss the impact of temperature on viscosity. How does temperature typically affect the flow of liquids?
I think it makes them flow easier, right?
Exactly! Higher temperatures usually reduce viscosity as it lessens intermolecular forces. This means the fluid molecules can move more freely.
What about gases? Does temperature have the same effect?
Good question! For gases, increasing temperature increases viscosity because it leads to more random molecular motions, enhancing momentum exchange.
So, it's opposite for gases and liquids?
Yes! Remember: 'Rise in Temp = Decrease in Viscosity for Liquids and Increase for Gases'.
That’s a tricky distinction!
It can be! Just keep practicing and recall the examples: syrup vs steam. Let’s summarize: higher temperatures typically lower viscosity for liquids, and increase it for gases.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the behavior of Newtonian fluids, highlighting key concepts such as viscosity, shear stress, and velocity gradients. It details the implications of temperature on viscosity and describes the difference between Newtonian and non-Newtonian fluids.
Detailed
Detailed Summary
In this section, we delve into the mechanics of Newtonian fluids, focusing primarily on how fluid behavior can be analyzed through the lens of shear stress and velocity gradients. A key aspect is the no-slip condition that introduces a linear velocity gradient between two parallel plates, where one is stationary and the other moves. This gradient leads to shear stress, which is proportional to the shear strain rate, profoundly illustrating Newton's law of viscosity. The discussion extends to how temperature influences viscosity, showing that while pressure changes do not greatly affect viscosity—especially in liquids—temperature variations significantly impact molecular motion and thus viscosity.
Furthermore, we distinguish between Newtonian and non-Newtonian fluids, stressing that Newtonian fluids maintain a constant viscosity regardless of the shear rate, while in non-Newtonian fluids, viscosity changes with the shear rate. The application of these principles is observable in everyday materials like paints, toothpaste, and oils, presenting a real-world context for these fluid mechanics concepts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Flow between Parallel Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress. Here what we consider that fluid element.
Detailed Explanation
In this section, we start by examining fluid flow between two parallel plates. The bottom plate has a velocity of zero, representing a stationary condition, while the top plate moves with velocity V. This setup creates a scenario where we examine how fluid behaves under sheer stress. Rather than focusing on molecular motion, we’re concentrating on the fluid as a cohesive unit, referred to as a 'fluid element'.
Examples & Analogies
Imagine a layer of honey spread between two plates. The top plate is like a spoon moving through the honey, while the bottom plate remains still. The honey next to the moving spoon starts flowing, while the honey next to the bottom plate stays put, creating a motion in the fluid.
Velocity Distribution within the Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A.
Detailed Explanation
Under the no-slip condition, the fluid's velocity is equal to the boundary plate it is in contact with. Therefore, at point A (the top plate), it moves with a velocity V, while at point B (the stationary plate), the velocity is 0. Between these two points, there’s a linear increase in velocity, meaning as you move from B to A, the fluid speed increases gradually.
Examples & Analogies
Picture a traffic jam where cars at the front are moving quickly, while those at the back are stationary. The cars gradually speed up as they approach the moving traffic, creating a smooth transition in velocity just like the fluid between the plates.
Deformation of Fluid Elements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After ∆t time these fluid element will be deformed as angular deformations will happen it that there will be angle θ will come at B and E, F and D.
Detailed Explanation
As time progresses, the fluid elements start to deform due to the differences in velocity between adjacent layers. This results in angular deformation, where the shapes of these fluid elements become distorted over time. The angular changes are represented as an angle θ, indicating how much the fluid has adjusted in response to shear stress.
Examples & Analogies
Think of a deck of cards being pushed at one end. The cards on the bottom do not move, but the cards at the top are pushed forward, causing the deck to bend and distort. This bending is similar to how the fluid elements deform under shear stress.
Velocity Gradient and Shear Stress Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This part indicates the velocity gradient. If I consider this is the y directions how the velocity varies along the y directions that is the constant which is equal to the shear strain rate.
Detailed Explanation
The velocity gradient refers to the rate at which velocity changes in the fluid as you move along the vertical axis (y-direction) between the two plates. This gradient is constant and equates to the shear strain rate, which helps us quantify how 'quickly' the fluid elements are deforming under shear stress. Essentially, a steeper gradient indicates a greater variation in velocity, leading to higher shear strains.
Examples & Analogies
Consider a slide at a playground: the steeper the slide (higher gradient), the faster kids slide down (higher velocity change). Similarly, in our parallel plates, where the gradient is steep, we experience greater stress and deformation in the fluid.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear stress is proportional to the shear strain rate and that is the Newton's laws of viscosity that shear strain is having a, this experimentally proved it.
Detailed Explanation
Newton’s law of viscosity states that the shear stress in a fluid is proportional to the shear strain rate, represented mathematically. This fundamental principle shows that as shear stress increases, so does the strain rate, demonstrating the fluid's resistance to deformation. This law is key to understanding how fluids behave under various flow conditions and reinforces the concept of Newtonian fluids.
Examples & Analogies
Think of spreading butter on bread: the harder you push the knife (increasing shear stress), the more the butter spreads (increasing strain rate). The relationship between your pressure and how easily the butter spreads illustrates Newton's law in action.
Effects of Temperature on Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us commit that how does the temperature effect on the coefficient of the viscosity. Now we have to look at the molecular levels okay.
Detailed Explanation
Temperature significantly affects the viscosity of fluids. As temperature rises, the molecular motion within liquids increases, reducing the intermolecular forces that hold the molecules together. This weakening leads to lower viscosity, meaning fluids flow more easily at higher temperatures. Conversely, in gases, increased temperature increases molecular motion which can lead to higher viscosity due to more collisions between molecules.
Examples & Analogies
A good example is cooking oil: when heated, it becomes thinner and easier to pour, showing how an increase in temperature decreases viscosity. Cold oil, in contrast, is thicker and harder to pour, demonstrating the effect of temperature on fluidity.
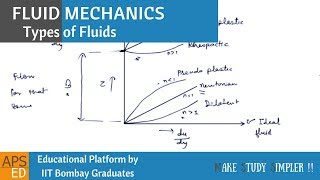
Classification of Fluids: Newtonian and Non-Newtonian
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The fluids that follow this relationship, this constant the proportionality relationship between the shear stress and the velocity gradient, we call them Newtonian fluids.
Detailed Explanation
Fluids are classified based on their response to shear stress. Newtonian fluids exhibit a constant viscosity, meaning their shear stress is directly proportional to shear rate. Examples include water and air. Non-Newtonian fluids, however, do not maintain this simple relationship as their viscosity can change with the rate of deformation. Examples include ketchup and toothpaste, which behave differently under varying shear conditions.
Examples & Analogies
Think of running water (Newtonian fluid), which flows steadily and predictably when you turn on a tap. Now imagine squeezing a tube of toothpaste (Non-Newtonian fluid); initially, it resists flow until sufficient force is applied, showcasing how different fluids respond to stress differently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Stress: The resistance encountered by a fluid due to deformation.
-
Velocity Gradient: The change in velocity of fluid layers as they move.
-
Newtonian Fluids: Fluids that exhibit constant viscosity with varying shear rates.
-
Non-Newtonian Fluids: Fluids whose viscosity depends on the shear rate.
-
Viscosity: The property of a fluid that measures its resistance to flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Syrup flowing slowly compared to water shows the concept of viscosity in action.
-
Toothpaste requires more force to squeeze out than water, demonstrating the non-Newtonian behavior of certain fluids.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Shear stress makes fluids flow, under force they start to go.
📖 Fascinating Stories
-
Imagine pushing honey in a jar; it slows down and resists just like a car. The temperature is key, it helps it roll, warmer makes it thinner, that’s the goal.
🧠 Other Memory Gems
-
Silly Viscosity: S for shear, V for velocity! Remember SS = μ × SG.
🎯 Super Acronyms
VISCO - Viscosity Influences Shear Change in Order.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
The force per unit area exerted by a fluid in response to deformation.
-
Term: Velocity Gradient
Definition:
The rate of change of velocity with respect to distance in the fluid.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow or deformation.
-
Term: Newtonian Fluid
Definition:
A fluid that maintains a constant viscosity regardless of the shear rate.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity changes with the shear rate.