Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Velocity Distribution
Unlock Audio Lesson
Today, we will discuss fluid flow through parallel plates. Picture one plate stationary and another moving with velocity V. Can anyone tell me what happens to the fluid between them?
The fluid will start moving, right? But the bottom layer doesn't move because it's next to the stationary plate.
Exactly! This phenomenon is governed by the no-slip condition. Now, from the stationary to the moving plate, how do you think the velocity changes?
It changes linearly, right? Like, at the bottom, it's zero and at the top, it's V.
Correct! This linear variation indicates a gradient in velocity. Remember the acronym 'VAG' - Velocity Affects Gradient. Who can summarize why this is important?
'VAG' helps us understand how shear stress develops in fluids between the plates!
Great job! The shear stress is linked to this velocity gradient.
Shear Stress and Strain
Unlock Audio Lesson
Now that we know about velocity, let's discuss shear stress. What happens as the fluid moves faster?
The shear stress increases as well since it's related to how quickly the fluid is deforming.
Exactly! This relationship indicates the shear strain rate, which we denote with a special symbol. Does anyone remember what shear stress is proportional to?
Shear strain rate! It's like how fast the layers of fluid are sliding past one another.
Correct! To remember this, think of the mnemonic 'SSSV' – Shear Stress is proportional to Shear Strain Velocity. How does this differ from solid mechanics?
In solid mechanics, stress relates to absolute strain, while here, it relates to the rate at which strain occurs.
Perfect! You've captured the essence of fluid mechanics.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Lesson
In our discussion of fluids, we need to distinguish between Newtonian and non-Newtonian fluids. Who can explain the difference?
Newtonian fluids have a constant viscosity, right? It doesn’t change when you alter the stress.
Exactly! And what about non-Newtonian fluids?
Their viscosity can change with the shear rate. Like how some paints become thicker when stirred fast.
That's right! For easy recall, think of 'NNV' – Non-Newtonian Viscosity varies. Can anyone give me an example of a non-Newtonian fluid?
Toothpaste! It doesn't come out until you squeeze it really hard!
Excellent example! Remember, understanding these differences helps us predict how fluids behave under various conditions.
Effects of Temperature on Viscosity
Unlock Audio Lesson
Let's explore how temperature influences viscosity. Who can tell me what generally happens to viscosity as temperatures increase?
Viscosity decreases because the molecules move more and lose some of their bonding forces.
Good! Remember 'WARM' – When temperature rises, viscosity must reduce. What about pressure effects?
Pressure doesn't significantly affect the viscosity of liquids, right?
Correct! Pressure changes may have minor effects, but not as noticeable as temperature. Keep this in mind.
So we focus more on temperature when discussing viscosity?
Exactly! The more we understand temperature effects, the better we can manage fluid flow applications.
Viscosity in Fluids
Unlock Audio Lesson
Finally, let's look at practical applications of viscosity in everyday fluids. Can anyone give examples?
Cooking oils have different viscosities, affecting how they coat food.
Also, car oil needs the right viscosity to ensure proper engine lubrication.
Great points! Viscosity plays crucial roles in many applications. To remember: 'CAVE' – Cooking oils, Automotive, Viscosity Matter Everywhere. Can we summarize what we learned today?
We learned about fluid flow through parallel plates, shear stress, temperature effects, and the types of fluids!
Excellent summary! Understanding these concepts will help you tackle fluid dynamics challenges ahead.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
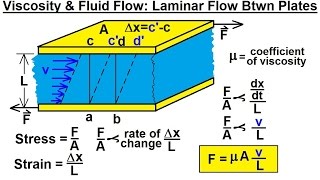
The section explains how fluid flows through parallel plates, detailing the velocity gradient, shear stress, and how these relate to Newton's laws of viscosity. Furthermore, it distinguishes between the behavior of Newtonian and non-Newtonian fluids in response to stress and strain rates.
Detailed
Fluid Flow Through Parallel Plates
In this section, we explore the flow of fluid between two parallel plates, where one plate is stationary while the other moves with a velocity, V. This creates a linear velocity gradient from the stationary plate to the moving plate, adhering to the no-slip condition. As fluid elements move from the stationary plate to the moving plate, angular deformations occur, leading to a relationship between shear stress and velocity gradient. The concept of shear strain rate, representing how the fluid deforms over time, is crucial.
We then delve into Newton's laws of viscosity, that state shear stress is proportional to the shear strain rate, an understanding that differentiates fluid mechanics from solid mechanics where stress is proportional to strain. Temperature and pressure effects on viscosity are crucial; while pressure changes don’t significantly affect viscosity, increases in temperature typically lower viscosity for liquids due to the decrease in intermolecular forces. The section concludes by categorizing fluids into Newtonian and non-Newtonian based on their response to applied stress.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Flow Between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
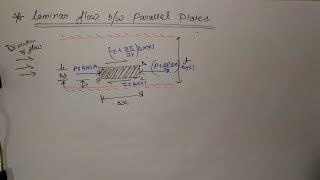
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress. Here what we consider that fluid element.
Detailed Explanation
This chunk introduces the scenario of fluid flow between two parallel plates. One plate is stationary (with zero velocity), while the other moves at a velocity 'V'. The term 'fluid element' refers to a volume of fluid we will analyze in this context. This setup is essential to understand how fluids behave under shear stress, which occurs when layers of fluid slide past each other.
Examples & Analogies
Think of it like two slices of bread with jam in between: if you spread the jam by pushing the top slice, the jam (fluid) gets sheared as the slices slide over each other, with one slice being stationary and the other moving.
Velocity Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means, I consider some space of A, B, C, D, this is what the fluid element. That means, whatever the fluids are there that reasons, I am defined as a fluid element. As you know it that at the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A.
Detailed Explanation
In this part, we define a fluid element between two points A and B. Because of the no-slip condition (where fluid adheres to the surfaces), the fluid at point A (the moving plate) moves at velocity V, while at point B (the stationary plate), the fluid is stationary with zero velocity. Consequently, the velocity of the fluid varies linearly between these two points. This linear relationship is crucial for understanding the gradient of velocity in fluids.
Examples & Analogies
Imagine a tapered slide; the top of the slide (point A) is where kids start sliding down (moving quickly), and the bottom (point B) is where they stop (no movement). The speed of the kids changes smoothly from fast to slow as they slide down.
Angular Deformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If as a linear velocity distribution as you assume it as we got it some of the parallel flow conditions after ∆t time these fluid element will be deformed as a angular deformations will happen it that there will be angle θ will come it at the B and E, F and D.
Detailed Explanation
After a time interval (∆t), the fluid element will experience deformation due to the velocity gradient. This means that the fluid element will no longer be rectangular but will instead become skewed, forming angles (θ) at certain points. This demonstrates how the motion of one plate influences the entire fluid element, leading to internal stresses and strains.
Examples & Analogies
Think of stretching a rubber band. As you pull it on one end, the rubber band gets thinner and longer, creating angular distortions in the shape. Similarly, as one plate moves, it stretches and distorts the fluid element.
Angular Deformation Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that is what will consider. Just rearranging that we can see that the rate of change of angular deformations of this fluid element is given by ∂θ/∂t = v / l.
Detailed Explanation
Here, we examine the rate of angular deformations in the fluid element. The equation derived shows that this rate depends on the constant velocity (v) and the thickness (l) of the plates. This relationship helps establish a quantitative measure of how shear stress affects the deformation rate within the fluid.
Examples & Analogies
Consider turning a steering wheel in a car. The speed at which you turn the wheel affects how quickly the wheels of the car turn. Similarly, how quickly the fluid deforms relates to the speed of the moving plate and the distance between the plates.
Velocity Gradient and Shear Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider this is the y directions how the velocity varies along the y directions that is the constant which is equal to the shear strain rate.
Detailed Explanation
The velocity gradient reflects how the fluid's velocity changes perpendicular to the direction of flow (along the y-axis). This gradient correlates directly with the shear strain rate, which measures how quickly the shape of the fluid changes over time. Understanding these concepts is vital in fluid mechanics as they lay the foundation for how shear stress is calculated.
Examples & Analogies
Imagine a stack of pancakes where each pancake is sliding on top of the one below it. The way the top pancake's speed varies compared to the stationary ones below it gives us insight into the shear rate just like how the velocity gradient shows changes in fluid flow.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But here, we are talking about the stress is proportionality to the strain rate. That means the change of the shear strain rate with respect to time, not the absolute value of the shear strain.
Detailed Explanation
This section introduces Newton's law of viscosity, which states that shear stress is directly proportional to the shear strain rate. In fluids, it’s important to focus on how quickly the fluid deforms (strain rate) rather than the total deformation. This principle distinguishes fluid behavior from solid materials, where stress correlates with deformation directly.
Examples & Analogies
Imagine pulling taffy; the force you apply and how fast the taffy stretches reflects the viscosity. The faster you pull, the more resistance you feel, akin to the shear strain rate.
Proportionality in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear strain is having a proportionality to the shear strain rate. Again I can emphasis that shear strain rate not the shear strain.
Detailed Explanation
This emphasizes the difference between shear strain (geometry of deformation) and shear strain rate (speed of deformation). In fluid dynamics, we often focus on the rate at which the deformation occurs because it directly impacts the fluid's behavior under shear stress.
Examples & Analogies
Think of a balloon being inflated; the rate at which the air is pumped affects how fast the balloon expands, rather than just how much larger it becomes overall.
Dynamic Viscosity and shear stress Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can define as τ = μ (∂u/∂y).
Detailed Explanation
This formula represents the relationship between shear stress (τ), dynamic viscosity (μ), and the velocity gradient (∂u/∂y). It summarizes how the fluid flows with respect to the force applied, establishing a direct relationship that is foundational in fluid mechanics.
Examples & Analogies
Think of pushing a thick syrup; the harder you push (more shear stress), the faster it flows. The viscosity indicates how resistant the syrup is to the push.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fluid Flow: The movement of liquid or gas between surfaces or through conduits.
-
Velocity Gradient: The rate at which velocity changes with respect to distance.
-
Shear Stress: The internal friction in a fluid acting parallel to an area.
-
Newtonian Fluids: Fluids that exhibit constant viscosity regardless of the shear rate.
-
Non-Newtonian Fluids: Fluids that display variable viscosity dependent on shear rate.
-
Shear Strain Rate: The rate at which a fluid deforms in response to shear stress.
-
Dynamic Viscosity: A measure of a fluid's resistance to flow, critical for understanding fluid behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing between two parallel surfaces experiences linear velocity growth from the stagnant surface to the moving surface.
-
When stirring honey, its resistance changes based on the rate of stirring, demonstrating non-Newtonian fluid behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a flow so fine, / Velocity's the line. / From slow to fast, / It helps us last.
📖 Fascinating Stories
-
Imagine a river splitting into two streams, one frozen still and the other rushing forward. The flow illustrates how speed changes and impacts everything in its path.
🧠 Other Memory Gems
-
Remember 'VAG' for Velocity Affects Gradient when thinking about flow between plates.
🎯 Super Acronyms
'NNV' for Non-Newtonian Viscosity varies based on the shear rate.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Gradient
Definition:
The change in velocity of fluid layers across a given distance, crucial for determining shear stress.
-
Term: Shear Stress
Definition:
The stress component parallel to a material cross-section, arising due to shear strain rate in fluids.
-
Term: Newtonian Fluid
Definition:
A fluid with a constant viscosity, unaffected by shear rates.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity changes with shear rate, resulting in varying flow behavior.
-
Term: Shear Strain Rate
Definition:
The rate at which deformation occurs in fluid due to applied shear stress.
-
Term: Dynamic Viscosity
Definition:
A measure of a fluid's resistance to flow, denoted by the symbol μ.
-
Term: Temperature Effect
Definition:
The influence of temperature changes on viscosity values in fluids.