Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Non-Newtonian Fluids
Unlock Audio Lesson
Today, we'll explore non-Newtonian fluids. Unlike Newtonian fluids, whose viscosity remains constant no matter the shear rate, non-Newtonian fluids display varied viscosity.
What does that mean for practical applications? How does it affect engineering?
Great question! In engineering, understanding fluid behavior is essential for design. For example, in paints, the viscosity decreases when stirred, making it easier to apply.
So, is this behavior also seen in other substances?
Yes! Toothpaste is another common example; it requires a certain amount of force to flow!
Remember, the acronym PSAT can help – Pseudoplastic, Shear thickening, Apparent viscosity, and Thinning. Let's keep that in mind!
So all these fluids behave differently under stress, right?
Exactly! Each type has unique properties that can significantly impact their performance in various applications.
In summary, understanding non-Newtonian fluids involves studying how they react to stress and determining their various types and applications.
Types of Non-Newtonian Fluids
Unlock Audio Lesson
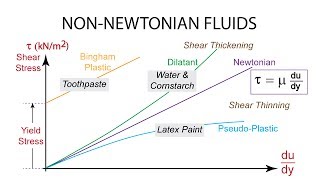
Let's dive deeper into the different types of non-Newtonian fluids. First, we have pseudoplastic fluids, which thin when a shear stress is applied.
Can you give an example of a pseudoplastic fluid?
Absolutely! Ketchup is one; it flows more easily once you shake or stir it. It's a great example of shear thinning.
What about dilatant fluids?
Dilatant fluids behave opposite to pseudoplastic ones—they thicken with increased shear stress. An example would be cornstarch mixed with water. When you apply a quick force, it doesn't flow easily!
So, these fluids actually change their viscosity depending on how fast they're moved, right?
Exactly! This concept can be memorable if we think of it as 'thinning' for pseudoplastic and 'thickening' for dilatant—just like their names imply.
In summary, we classified non-Newtonian fluids into pseudoplastics and dilatants based on how they behave under different shear conditions.
The Importance of Shear Stress and Strain Rate
Unlock Audio Lesson
Let's discuss how shear stress and strain rates influence the behavior of non-Newtonian fluids.
Why is shear rate so significant?
Great question! The shear rate directly affects viscosity in non-Newtonian fluids. The slope of the stress-strain curve helps us understand this dynamic.
Are there mathematical expressions we use for this?
Yes! The general relation can be expressed as shear stress equals the viscosity times the shear gradient. It's essential to grasp how these interact.
So can we measure the viscosity at different shear rates for these fluids?
Absolutely! Measuring the apparent viscosity at various shear rates is crucial to characterizing non-Newtonian fluids.
In summary, the shear stress and strain rate relationship is critical to understanding and applying non-Newtonian fluid concepts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the behavior of non-Newtonian fluids is explored, particularly how their shear stress relationship deviates from that of Newtonian fluids. Key distinctions are made between different types of non-Newtonian fluids, such as pseudoplastic and dilatant fluids, and the key factors influencing their viscosity and flow behavior are discussed.
Detailed
In this section, we delve into the concept of non-Newtonian fluids and examine the fundamental differences between these fluids and traditional Newtonian fluids. Specifically, we analyze how stress correlates with strain rates in non-Newtonian fluids, explaining that their behavior could vary significantly based on the rate of deformation. While Newtonian fluids maintain a consistent viscosity regardless of strain rates, non-Newtonian fluids display varying viscosity, characterized by types such as pseudoplastic and dilatant fluids. We observe phenomena such as shear thickening and thinning and focus on real-world applications and implications of these behaviors, emphasizing the importance of understanding viscosity change in different conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Flow Between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress. Here what we consider that fluid element. That means, I consider some space of A, B, C, D, this is what the fluid element.
Detailed Explanation
This chunk discusses the concept of fluid flow between two parallel plates where one plate is stationary, and the other is moving. It sets the stage for understanding shear stress by defining a 'fluid element' as the space between these plates. At one point (Point B), the fluid has zero velocity, while at the other point (Point A), the fluid has a velocity 'V'. This arrangement allows us to visualize how velocity changes across the gap between the plates.
Examples & Analogies
Think of a sandwich with peanut butter where one slice of bread is held in place while the other is being spread with a knife. The peanut butter moves with the knife, creating a flow while the bottom slice remains stationary. Here, the peanut butter is the fluid, and the slices of bread represent the plates.
Velocity Profile Between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it that at the A point we will have the velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it, it will have a linear velocity variation from B to A. That linear velocity from zero to V as the y increases, the velocity will increase it and maximum velocity will be the V.
Detailed Explanation
The velocity profile of the fluid is described as linear between the two points (A and B) due to the no-slip condition, meaning the fluid at Point B (the stationary plate) has zero velocity, while at Point A (the moving plate), it reaches the maximum velocity 'V'. Hence, as we move from the stationary plate towards the moving plate, the velocity of the fluid increases in a linear manner.
Examples & Analogies
Imagine riding a slide. At the starting point (the top), you are at rest (zero velocity), but as you slide down (towards the bottom), you pick up speed. The increase in speed is consistent, similar to how fluid velocity increases linearly between the two plates.
Angular Deformation of Fluid Elements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After ∆t time these fluid element will be deformed as angular deformations will happen it that there will be angle θ will come it at the B and E, F and D. That is a new positions of the fluid element after ∆t time. Similar way the θ at this point. So consider a very simple geometry of these problems. I can consider these distance of AE is V into delta t divided by l will be the tan θ.
Detailed Explanation
This chunk discusses how, after a certain time (∆t), the fluid elements experience angular deformation due to the shear caused by the movement of the top plate. The deformation results in an angle (θ) at points where the fluid has been displaced. The calculation of this angle involves the fluid's velocity and the distance between the plates.
Examples & Analogies
Consider a piece of clay that you are stretching. If you pull the top of the clay in one direction while keeping the bottom stationary, the shape of the clay changes. The change in shape represents angular deformation similar to how fluid elements behave between the plates.
Viscosity and Shear Strain Rate Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear strain rate and the velocity gradient are equal for these conditions. The shear rate strain rate is defined as ∂u/∂t dy. These parallel flow conditions when you have velocity is linear distributions, the shear strain rate and the velocity gradient they are equal.
Detailed Explanation
In non-Newtonian fluid mechanics, it's essential to understand the relationship between shear strain rate and velocity gradient. Under constant conditions, when fluid flows between the plates, the rate at which the fluid deforms (shear strain rate) is equal to the rate of change of velocity across the distance (velocity gradient). This indicates how quickly the velocity is changing as you move away from the stationary plate.
Examples & Analogies
Picture spreading butter on toast. The rate at which the butter spreads (how quickly it deform) is directly related to how fast you are moving the knife (velocity gradient). As you push the knife more quickly, the butter strains and spreads more, showing a similar relationship to fluid flow.
Newton's Laws of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The stress having the proportionality with the strain. Here, we are talking about the stress is proportionality to the strain rate, indicating a basic distinction between fluid and solid mechanics.
Detailed Explanation
This part encapsulates Newton's laws of viscosity, where shear stress in fluids is directly proportional to the shear strain rate. This is a critical difference from solid mechanics, where stress is proportional to strain. In fluids, as the rate of deformation increases, so does shear stress, evidencing a dynamic relationship in non-Newtonian fluids.
Examples & Analogies
Think about a sponge versus a rock. When you press hard on a sponge (fluid), it compresses easily (strain), and if you press faster (strain rate), it also resists more (stress) compared to a rock that just fractures under pressure. This illustrates the differences in behavior under stress for fluids and solids.
Behavior of Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We define the non-Newtonian fluids based on their behavior: shear thickening fluids, which require more force as deformation rate increases, and shear thinning fluids, which become easier to deform under increasing shear.
Detailed Explanation
Non-Newtonian fluids can behave differently under stress compared to Newtonian fluids. Shear thickening fluids become more viscous when stirred or mixed faster, requiring more effort to move. Conversely, shear thinning fluids are easier to stir as you increase the flow rate or movement. Understanding these behaviors is essential in various applications where flow characteristics change with force.
Examples & Analogies
Consider cornstarch mixed with water, often referred to as oobleck. When you gently press or stir it, it flows easily (shear thinning), but if you push it hard, it becomes solid-like (shear thickening). This behavior perfectly illustrates the unique properties of non-Newtonian fluids.
Effects of Temperature on Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
How does the temperature effect on the coefficient of the viscosity? The viscosity generally decreases with increasing temperatures for liquids due to reduced intermolecular forces.
Detailed Explanation
Temperature has a significant impact on fluid viscosity. As temperature increases, the kinetic energy of fluid molecules increases, meaning they move around more and the forces holding them together weaken. For liquids, this results in decreased viscosity as they flow more easily. In contrast, gases may exhibit increased viscosity with higher temperatures due to increased molecular collisions.
Examples & Analogies
Imagine how honey behaves. When it's cold, honey flows slowly, but if you heat it up, it pours out much more readily. The decrease in viscosity with temperature makes it easier for the honey to flow, showcasing how temperature influences fluid behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Stress: The force per unit area applied parallel to the surface.
-
Viscosity: A measure of a fluid's resistance to flow.
-
Pseudoplastic Behavior: Decrease in viscosity with increased shear rate.
-
Dilatant Behavior: Increase in viscosity with increased shear rate.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Ketchup is a pseudoplastic fluid; it flows more easily when shaken.
-
Cornstarch mixed with water behaves as a dilatant fluid, thickening when rapidly stirred.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In ketchup, smoothness rules the quest, shake it up, it flows the best.
📖 Fascinating Stories
-
Imagine a painter mixing paint: With just a little force, it flows, but rapid stirring makes it thicken—a dance of viscosity!
🧠 Other Memory Gems
-
Remember PSAT for non-Newtonian fluids: Pseudoplastic, Shear thickening, Apparent viscosity, Thinning.
🎯 Super Acronyms
PNN - Pseudoplastic and Newtonian Neuroplasticity!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NonNewtonian Fluids
Definition:
Fluids whose viscosity changes with the shear rate, displaying behaviors different from Newtonian fluids.
-
Term: Pseudoplastic Fluids
Definition:
A type of non-Newtonian fluid that decreases in viscosity when shear stress is applied.
-
Term: Dilatant Fluids
Definition:
A type of non-Newtonian fluid that increases in viscosity when shear stress is applied.
-
Term: Apparent Viscosity
Definition:
The viscosity of a non-Newtonian fluid as it changes with shear rate.