Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Mechanics
Unlock Audio Lesson
Today, we are going to discuss fluid mechanics, particularly focusing on Newtonian and non-Newtonian fluids. Can anyone define what a fluid is?
I think a fluid is anything that can flow, like liquids and gases.
Exactly! Fluids are substances that can change shape easily without a fixed structure. Now, what do you think makes Newtonian fluids special?
Is it because they have a constant viscosity?
Correct! Newtonian fluids maintain constant viscosity regardless of the shear rate. A key point to remember is that shear stress is proportional to the shear strain rate. We can think of it as the equation σ = μ * (du/dy). Does anyone remember what each symbol represents?
σ is shear stress, μ is viscosity, and (du/dy) is the velocity gradient!
Great job! Let's summarize: Newtonian fluids are characterized by a linear relationship between shear stress and shear strain rate.
Exploring Non-Newtonian Fluids
Unlock Audio Lesson
Moving on, let's discuss non-Newtonian fluids. What do you think happens to their viscosity when they’re subjected to stress?
I believe it changes, right? It's not constant!
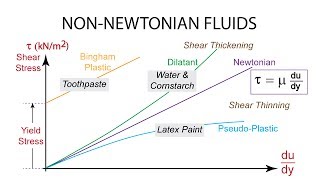
Correct! Non-Newtonian fluids exhibit changes in viscosity depending on the shear rate. Can anyone give examples of non-Newtonian fluids?
Toothpaste seems to be one. It doesn't come out unless you apply a certain amount of force.
Exactly! Toothpaste is a Bingham plastic, which requires a yield stress to start flowing. It only deforms when that stress is exceeded.
What about the shear-thinning fluids like ketchup?
Great example! Shear-thinning fluids decrease in viscosity with increased shear rate. This 'thinning' behavior is common in many everyday substances.
So, is there a relationship we can see on a graph?
Yes! The graph will show the slope representing the apparent viscosity. We will visualize this in upcoming exercises.
Effects of Temperature and Pressure
Unlock Audio Lesson
Next, let’s discuss how temperature impacts the viscosity of fluids. Who can tell me how temperature affects liquids?
I think increasing the temperature decreases the viscosity of liquids.
That's right! As the temperature rises, molecular motion increases, leading to weaker intermolecular forces and thus lower viscosity. How do you think pressure impacts viscosity?
I believe increasing pressure has a minimal effect on liquids but can slightly affect gases.
Exactly! For liquids, pressure changes have little effect on viscosity, but for gases, increased pressure can enhance molecular interactions, slightly affecting the viscosity.
So, as temperature increases, gas viscosity rises?
Correct! Gases generally show increased viscosity with rising temperature. Remember, in contrast to liquids, the molecular motion dominates here.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the principles of fluid mechanics as they relate to Newtonian and non-Newtonian fluids. Newtonian fluids maintain a constant viscosity regardless of shear rate, while non-Newtonian fluids exhibit varying viscosity under different conditions. The effects of temperature and pressure on the viscosity of fluids are also examined.
Detailed
Summary of Newtonian and Non-Newtonian Fluids
In this section, we delve into the concepts of Newtonian and non-Newtonian fluids, focusing primarily on how shear stress relates to shear strain rate. Newtonian fluids have a consistent viscosity that does not change with the rate of shear, while non-Newtonian fluids display variable viscosity that depends on how quickly they are deformed. The relationship between shear stress and shear strain is linear for Newtonian fluids, represented by the equation σ = μ * (du/dy), where σ is shear stress, μ is viscosity, and (du/dy) is the velocity gradient.
The section further discusses how temperature and pressure affect the viscosity of fluids, revealing that increasing temperature decreases viscosity in liquids due to weakened intermolecular forces, while for gases, viscosity typically increases with temperature due to enhanced molecular motion. We also explore special cases of fluids like Bingham plastics and shear-thinning/ shear-thickening fluids, emphasizing their unique behaviors under different conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Flow Between Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress. Here what we consider that fluid element.
That means, I consider some space of A, B, C, D, this is what the fluid element. That means, whatever the fluids are there that reasons, I am defined as a fluid element.
Detailed Explanation
In this chunk, we explore fluid flowing between two parallel plates. One plate is stationary (velocity = 0), while the other moves with a velocity V. This creates a scenario where the velocity of the fluid is not uniform. At point A (near the moving plate), the fluid has a high velocity, while at point B (near the stationary plate), the velocity is zero due to the no-slip condition. The flow in between results in a linear increase in fluid velocity as we move from point B to point A.
Examples & Analogies
Imagine spreading butter on a piece of bread with a knife. The knife is like the moving plate, and the butter represents the fluid. The butter close to the knife moves quickly, while the butter farther from the knife stays still until you apply more pressure. This helps visualize how fluid layers slide over each other due to different velocities.
Velocity Gradient and Shear Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So next one is the velocity lesser than that or above one will go moving with the fluid is more than that. So if as a linear velocity distribution as you assume it as we got it some of the parallel flow conditions after ∆δt time these fluid element will be deformed as a angular deformations will happen it that there will be angle δ will come it at the B and E, F and D.
Detailed Explanation
As the fluid continues to flow, after a time interval (∆t), the fluid element will deform. This deformation can result in a change in the shape of the fluid element, indicated by angular deformations at points B and D. The fluid's behavior can be analyzed using the concept of velocity gradient, which describes how velocity changes with distance across the gap between the two plates.
Examples & Analogies
Consider rolling dough with a rolling pin. As you apply pressure, the dough doesn’t just slide; it stretches and deforms. Similarly, as the fluid flows, it deforms, demonstrating how the flow of different layers interacts.
Newton's Law of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if I consider the at the y distributions and the angular velocity distributions if I consider it I will get it the u, the velocity at these points and ratio of the distance as a linear velocity distributions concept, we can get it,
√ V / y .
We remember this is what is indicating us is that the velocity gradient. If I consider this is the y directions how the velocity varies along the y directions that is the constant which is equal to the shear strain rate.
Detailed Explanation
Newton's law of viscosity relates shear stress to the shear rate (velocity gradient). It states that shear stress (τ) is proportional to the velocity gradient, represented mathematically as τ = μ (du/dy), where μ is the dynamic viscosity. This indicates that in fluids, shear stress increases with the rate at which the velocity changes from one layer of fluid to another.
Examples & Analogies
Think of honey pouring from a bottle. It flows slowly due to its high viscosity compared to water. If you were to apply a force (like shaking), the honey moves more easily. This resistance to flow at different rates illustrates how viscosity affects the behavior of fluids under stress.
Differences Between Fluid Mechanics and Solid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we are coming to the exactly the solid mechanics concept the stress having the proportionality with the strain. But here, we are talking about the stress is proportionality to the strain rate. That means the change of the shear strain rate with respect to time, not the absolute value of the shear strain.
Detailed Explanation
In solid mechanics, stress is proportional to strain (the deformation of the material). However, in fluid mechanics, stress is proportional to the rate of strain (shear strain rate). This distinction shows how fluids respond differently to stress compared to solids; fluids can flow and change shape continuously, whereas solids have fixed shapes until a certain limit.
Examples & Analogies
Imagine pushing on a rubber ball. It deforms under your pressure (strain), but if you stop pushing, it returns to its original shape. In contrast, when you apply pressure to water in a container, it simply moves and takes the shape of the container without returning to a ‘resting’ state.
The Effect of Temperature on Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us commit that how how does the temperature effect on the coefficient of the viscosity. Now we have to look at the molecular levels okay. So if you look at this molecular levels, when you talk about the liquids, they will have a molecular bonding forces between two molecules okay. But that is much weaker when talk about the gases.
Detailed Explanation
Temperature affects viscosity significantly. For liquids, as temperature rises, molecular motion increases, which reduces the cohesive forces between molecules. This decrease in interaction results in lower viscosity. Conversely, for gases, increasing temperature increases the random motion of molecules, which can lead to an increase in viscosity as the gas particles become more active.
Examples & Analogies
Consider making ice tea. When you add ice to hot tea, the sugar dissolves more slowly due to higher viscosity at lower temperatures. Yet if you were to heat the tea, the sugar dissolves rapidly, showcasing how temperature changes a liquid’s viscosity.
Types of Fluids: Newtonian vs. Non-Newtonian
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the fluids those follow this relationship, this constant the proportionality relationship between the shear stress and the velocity gradient, we call them Newtonian fluids, okay. Those fluid flow problems we call the Newtonian fluids. That means what the coefficient of viscosity which is a directly proportionality constant, that does not vary as the rate of deformations are, or the time is changing.
Detailed Explanation
Newtonian fluids are defined by their consistent viscosity that does not change, regardless of the shear rate. Common examples include water and air, where the relationship between shear stress and flow remains linear. Non-Newtonian fluids (like ketchup or toothpaste) don’t have a constant relationship; their viscosity can change with the applied stress or rate of deformation.
Examples & Analogies
Think of stirring maple syrup versus water. Maple syrup is thick (non-Newtonian) and requires more energy to stir; its flow changes under different forces, while water (Newtonian) flows smoothly, maintaining its viscosity regardless of the force applied.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Newtonian Fluid: These fluids exhibit constant viscosity regardless of shear rate.
-
Non-Newtonian Fluid: These fluids demonstrate variable viscosity depending on the shear rate.
-
Viscosity: A measure of a fluid's resistance to flow, essential in discussing fluid behavior.
-
Shear Stress and Velocity Gradient: The relationship between these two concepts defines how fluids respond to external forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water is a classic example of a Newtonian fluid because its viscosity remains constant under different flow conditions.
-
Toothpaste is a non-Newtonian fluid demonstrating Bingham plastic behavior; it requires force for flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fluid, there it flows, Newton's rules are how it goes.
📖 Fascinating Stories
-
Imagine a river (Newtonian) that flows steadily without changing its shape, while a smoothie (non-Newtonian) thickens when blended harder.
🧠 Other Memory Gems
-
Think of 'N.E. Viscous' - Newtonian Equals Viscosity Constant; Non-Newtonian Varies!
🎯 Super Acronyms
Remember 'V.S.N.' for 'Viscosity Shows Nature' to describe fluid behaviors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the shear rate applied.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity changes with different shear rates.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow.
-
Term: Shear Stress (σ)
Definition:
The force per unit area exerted by a fluid parallel to a surface.
-
Term: Velocity Gradient (du/dy)
Definition:
The rate of change in velocity across a fluid layer.
-
Term: Shear Strain Rate
Definition:
The rate of deformation of a fluid element due to shear stress.
-
Term: Bingham Plastic
Definition:
A type of non-Newtonian fluid that requires a finite yield stress to start flowing.
-
Term: Shear Thinning
Definition:
A property of non-Newtonian fluids where viscosity decreases with increasing shear rate.
-
Term: Shear Thickening
Definition:
A property of non-Newtonian fluids where viscosity increases with increasing shear rate.