Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Fluid Flow Between Parallel Plates
Unlock Audio Lesson
Today, we’re going to discuss fluid flow characteristics between two parallel plates, specifically how velocity changes across the flow area. Can anyone tell me what happens to fluid velocity when it flows past a stationary surface?
The fluid velocity is zero at the stationary surface because of the no-slip condition.
Exactly! The no-slip condition indicates that the fluid adheres to the stationary plate. If the top plate moves with velocity V, what can we infer about the velocity of the fluid in between?
The fluid velocity increases linearly from zero at the stationary plate to V at the moving plate!
Great observation! This defines the velocity gradient, which is crucial for understanding shear stress in flowing fluids.
What exactly do we mean by shear stress here?
Shear stress occurs when forces are applied parallel to the surface of an object. In our case, it results from the velocity gradient we just discussed. Remember it as 'shear stress is proportional to velocity change' — let’s call this the 'Velocity-Shear Principle'!
So it’s like the more the plates move apart in terms of speed, the more shear stress there will be?
Exactly, Student_4! In short, the amount of shear stress can be calculated as the product of viscosity and the velocity gradient. Excellent contributions today!
Newton's Law of Viscosity
Unlock Audio Lesson
Now, let’s explore Newton’s law of viscosity. What have you learned about how shear stress relates to viscosity?
I think it’s a proportional relationship — shear stress equals viscosity times the velocity gradient.
Correct! This relationship defines Newtonian fluids where the shear stress is directly proportional to the shear strain rate, contrary to non-Newtonian fluids.
What makes a fluid Newtonian versus non-Newtonian?
Good question! Newtonian fluids maintain a constant viscosity regardless of the shear rate, while non-Newtonian fluids have a viscosity that changes with the shear rate.
Can you give an example of a non-Newtonian fluid?
Certainly! Things like ketchup are examples; they become runnier when shaken, possessing a shear-thinning property. Keep in mind the term 'apparent viscosity' for such cases.
This is really fascinating! So viscosity and shear stress affect how fluids flow in different scenarios.
Exactly, understanding this principle will aid us in real-world applications and analyses. Well done, everyone!
Impact of Temperature on Viscosity
Unlock Audio Lesson
Let’s delve into how temperature variations affect viscosity. Who can explain what happens to a fluid's viscosity with temperature changes?
For liquids, increasing the temperature decreases viscosity, right?
That’s spot on! The increased kinetic energy weakens intermolecular forces, making it easier for layers to slide over one another. And for gases?
I think the viscosity increases with temperature in gases because they become more energetic and can collide more often?
Exactly! This highlights the contrasting behavior of liquids and gases. Remember: 'Liquid viscosity decreases; gas viscosity increases with temperature' as a simple mnemonic!
That is helpful! So, can we approach viscosity measurement experimentally?
Yes! Techniques like the Sutherland correlation provide experimental data to quantify changes in viscosity relative to temperature.
It all makes sense now! Thank you for clarifying!
You're all doing wonderfully. Keep these principles in mind for your lab exercises and real-world examples!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on fluid flow through parallel plates, emphasizing the velocity gradient and its relation to shear stress. It highlights Newton's laws of viscosity and discusses how temperature and pressure affect the coefficient of viscosity for liquids and gases.
Detailed
In this section, we explore the dynamic behavior of fluids between parallel plates, focusing on the velocity gradient as modeled in fluid mechanics. When considering one stationary plate and another moving plate, the fluid experiences a linear velocity variation that results in shear stress due to the no-slip condition. We derive the connection between shear strain rate and the velocity gradient, establishing that the shear stress is directly proportional to the strain rate, thus laying the groundwork for Newton's law of viscosity.
We also address how temperature affects the viscosity of fluids, noting that for liquids, increased temperature results in decreased viscosity due to weaker intermolecular bonds, while the opposite effect is seen in gases where higher temperatures increase kinetic activity and therefore viscosity. The section concludes with applications and examples, illustrating the concepts of Newtonian and non-Newtonian fluids as they apply in real-world scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Flow Through Parallel Plates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
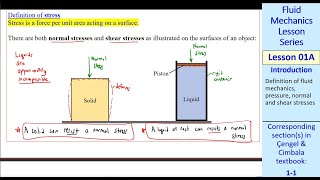
If I consider the same fluid flow through a parallel plate, okay. One of the plate the velocity is zero which is at the rest conditions and other the top plate is moving with a velocity V. So as a microscopic point of view I am not talking about the molecular motions or exchange of the molecular motions or the momentum flux that what is resulting a shear stress.
Detailed Explanation
This chunk introduces the concept of fluid flow between two parallel plates—one at rest and the top one moving with velocity V. In this scenario, we are going to analyze how the motion of the top plate affects fluid flow, particularly focusing on shear stress without concerning ourselves with molecular details of the fluid.
Examples & Analogies
Imagine you have a sandwich with peanut butter spread between it. The bottom slice of bread is stationary while you spread the top slice across the peanut butter. The way the peanut butter spreads and changes shape illustrates how fluid flows and deforms under shear stress due to the movement of the top plate.
Velocity Distribution in Fluid Elements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Here what we consider that fluid element. That means, I consider some space of A, B, C, D, this is what the fluid element. As you know, at the A point we will have velocity V as the no-slip conditions. At the B point we will have velocity zero. So velocity assuming it will have a linear velocity variation from B to A.
Detailed Explanation
In this chunk, we define what a fluid element is and how to visualize the velocity distribution across this fluid. Point A, closer to the moving plate, has a velocity V, while point B, resting against the stationary plate, has a velocity of 0. This results in a linear change in velocity from B to A, describing a smooth gradient.
Examples & Analogies
Think of a slide that is smooth at the top (high velocity) and gradually becomes rough at the bottom (low or no velocity). As you slide down, you would speed up initially, but if you were to encounter a rough patch, your speed would drop, just like how fluid velocity changes between the plates.
Angular Deformations in Fluid Elements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If as a linear velocity distribution as you assume it as we got it some of the parallel flow conditions after ∆t time these fluid element will be deformed as angular deformations will happen.
Detailed Explanation
This part discusses how, after a small time interval (∆t), the fluid element (A, B, C, D) will undergo angular deformations due to the shear stress caused by the velocity difference between the two plates. This deformation can be quantitatively analyzed to understand how the fluid behaves under shear conditions.
Examples & Analogies
Consider stretching a rubber band. If you pull on it, it undergoes deformation and changes shape. In analogy, the fluid element deforms in response to varying forces around it, just as the rubber band changes shape under tension.
Velocity Gradient and Shear Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We remember this is what is indicating us is that the velocity gradient. If I consider this is the y directions how the velocity varies along the y directions that is the constant which is equal to the shear strain rate.
Detailed Explanation
Here we focus on the concept of the velocity gradient, which is the rate of change of velocity over distance (in this case, the y-direction). The velocity gradient within the fluid corresponds to the shear strain rate, which is a valuable concept in fluid mechanics for understanding how fluids deform under stress.
Examples & Analogies
Imagine you are mixing a thick paint with a stick. The faster you stir, the more the paint changes its shape and flows. The change in the paint’s resistance to flow and its velocity with respect to your stirring speed is similar to how velocity gradients work in fluids.
Newton's Laws of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But here, we are talking about the stress is proportional to the strain rate. That means the change of the shear strain rate with respect to time, not the absolute value of the shear strain.
Detailed Explanation
This section introduces Newton's laws of viscosity, which highlight the relationship between shear stress and shear strain rate. For fluids, it is key to distinguish that shear stress is proportional to the rate of deformation (strain rate) over time, unlike in solid mechanics where it is proportional to shear strain itself.
Examples & Analogies
Think of how honey flows slowly when poured, compared to water which flows quickly. Honey exhibits a higher viscosity; thus, it has a greater resistance to flow and deformation compared to water due to how quickly their shear rates change under force.
Effects of Temperature on Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us commit that how does the temperature effect on the coefficient of the viscosity. Now we have to look at the molecular levels okay.
Detailed Explanation
In this chunk, we analyze how temperature impacts viscosity. The concept is that, as temperature increases, the kinetic energy of the molecules in a fluid increases, which affects intermolecular bonding and results in variations in viscosity.
Examples & Analogies
Imagine how syrup becomes runnier when heated. At high temperatures, molecular movements increase, causing less resistance to flow. This transformative effect is what happens to all fluids, including water or oil, as temperatures rise.
Comparison of Viscosity in Liquids and Gases
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you increase the temperature which manifests to the molecular motions to sustain that temperatures. In that conditions what it will happen it, it will reduce the binding force, the intermolecular binding force between two molecules.
Detailed Explanation
The chunk compares the behavior of liquids and gases under temperature changes. In liquids, increased temperatures generally decrease viscosity due to the reduction in intermolecular forces, while gases exhibit an opposite trend and require less force to flow as temperature increases. Understanding how viscosity varies systematically across states of matter enhances grasp on fluid dynamics.
Examples & Analogies
Consider blowing up a balloon. In warm air, the balloon expands easily, demonstrating how gas viscosity decreases as temperature increases. In contrast, liquids like oil become easier to pour when heated, showing a similar reduction in viscosity.
Viscosity and Fluids: Newtonian vs. Non-Newtonian
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Those fluid flow problems we call the Newtonian fluids, okay. That group of the fluid flow problems we call Newtonian fluids, where you have the shear stress causing by any shear forces is directly proportional to the velocity gradient or the shear strain rate.
Detailed Explanation
This last chunk distinguishes between Newtonian fluids, which obey the simple rule of viscosity (shear stress is proportional to shear rate), and non-Newtonian fluids, where this relationship can vary. Evaluating different fluid types based on their viscosity behavior is crucial in multiple engineering applications.
Examples & Analogies
Think of classic Newtonian fluids as water flowing easily and predictably down a drain. In contrast, a non-Newtonian fluid like cornstarch mixed with water (oobleck) behaves differently; it can act rigid under fast movement and liquid when moving slowly, showcasing the nature of non-Newtonian behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Gradient: The rate at which fluid velocity changes across a distance.
-
Shear Stress: The force that acts parallel to the surface of an object in motion.
-
Viscosity: The internal friction of a fluid that resists flow.
-
Newtonian Fluids: Fluids that have a constant viscosity regardless of the shear rate.
-
Non-Newtonian Fluids: Fluids whose viscosity changes with the shear rate.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing through a pipe at different temperatures to see how viscosity affects flow rate.
-
The behavior of ketchup when shaken, demonstrating non-Newtonian characteristics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Shear stress grows with the velocity's flow, a sticky struggle, slow and low.
📖 Fascinating Stories
-
Once upon a time, in a kingdom of fluids, Water swiftly flowed like a dance, while Ketchup thickened, needing more force to enhance! This tale hints at their viscosity's might!
🧠 Other Memory Gems
-
For Viscosity: 'V Flowers - Vis and Phlo' (Viscosity and Flow) to remember they're connected!
🎯 Super Acronyms
VISC - Viscosity Increases with Shear Change (reminder for non-Newtonian fluids).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Gradient
Definition:
The rate of change of velocity with respect to distance in a fluid, pivotal for determining shear stress.
-
Term: Shear Stress
Definition:
The force per unit area induced by the movement of fluid layers relative to each other.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow, which varies with temperature and pressure.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the shear rate.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity changes with the shear rate, exhibiting unique behaviors under stress.
-
Term: Shear Strain Rate
Definition:
The rate of deformation experienced by fluid layers which quantifies how quickly the deformation occurs.
-
Term: Sutherland Correlation
Definition:
An empirical relationship describing how the viscosity of gases changes with temperature.