Dimensional Analysis and Experimental Data
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Velocity Defect Concept
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will start by understanding the concept of velocity defects. Can anyone explain what we mean by a velocity defect?

Is it the difference between the average velocity and local velocity at a specific point?

Exactly! The velocity defect represents how much the local velocity deviates from the average velocity. Think of it as a measure of turbulence.

How does this relate to the energy losses in pipes?

Great question! Energy losses due to friction in pipes are closely related to velocity defects. High turbulence can lead to greater energy losses.

Are there equations to quantify these losses?

Yes! We'll cover those shortly, but first, remember the acronym 'VDF' – Velocity Defect Formula – to help recall our discussions around this concept.

So, the key takeaway here is that knowing the velocity defect helps us in dimensional analysis of flow through pipes. Let’s proceed to the relevant equations.
Dimensional Relationships in Fluid Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's explore how we can use dimensional analysis to derive relationships between different flow parameters. Can anyone share what parameters might be involved?

I think the height, pipe diameter, and velocity would be involved.

Excellent! We also often refer to shear velocity in these relationships. Remember, in turbulent flows, these parameters are interdependent.

Can you explain what shear velocity is?

Sure! Shear velocity is a measure of the velocity scale for turbulent flows and is crucial for analyzing turbulence characteristics. It might help to think of the acronym 'SV' for Shear Velocity when studying these concepts.

The relationship can be summarized as V ∝ h/W, where W represents additional factors that affect flow. Understanding these relationships allows us to predict how changes in one variable can affect others.

In summary, dimensional analysis helps us visualize and quantify our understanding of fluid flow dynamics.
Application: Pipe Flow in Series
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s talk about pipes in series. Can someone tell me how the flow behaves in such configurations?

I think the discharge is constant across all pipes, right?

Correct! Q1 = Q2 = Q3 indicates steady flow through each section. But energy losses can vary—is anyone familiar with the concept of head loss?

Isn’t it the total energy loss due to friction and other minor factors?

Absolutely! There are major losses due to friction, but we also must consider minor losses related to factors like changes in diameter. The combined total gives us the total head loss.

How do we compute those losses?

We add up individual losses from each pipe. Remember the mnemonic 'M + m = Total Loss' where M is major losses and m is minor losses. Understanding these helps in designing efficient piping systems!

In summary, energy conservation in pipes requires all losses to be accounted for, especially in series configurations.
Application: Pipe Flow in Parallel
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s shift our focus to parallel pipes. How does flow divide across multiple paths?

I think the flow divides based on the resistance in each path.

Exactly! Each path must have equal energy losses as the flow splits and combines again. Remember the key phrases 'Equal Loss, Equal Flow.'

Does that mean the head losses for each pipe are the same?

Correct! This principle of equal losses helps ensure the flow is balanced across all paths. If one path is obstructed, it directly impacts the flow rates in the others.

So, in summary, by analyzing head losses, we can efficiently manage parallel pipe flows.

Great recap! Efficient management ensures optimal performance in engineering applications.
Solving Real-world Problems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we conclude, let’s apply what we’ve learned to real-world problems. Can anyone suggest any scenarios we've discussed?

I think the example where we calculate head losses for a two-kilometer pipe is a good start.

Absolutely! We can calculate energy losses using the relevant equations. Let’s remember the formula for head loss due to friction: h = f*(L/D)*(V^2/2g).

What does each variable represent?

'f' is the friction factor, 'L' is the pipe length, 'D' is the diameter, 'V' is the velocity, and 'g' is acceleration due to gravity. Keeping them aligned helps with calculations.

How do we ensure these calculations are accurate?

By using relevant data from experiments, such as the Nikuradse examples we mentioned, we can validate our results. Keep revisiting the relationship between these variables as well!

In summary, understanding the core principles of dimensional analysis allows for effective problem-solving in hydraulic engineering!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section emphasizes the use of dimensional analysis to determine relationships between variables in fluid mechanics, especially concerning velocity defects in turbulent flow scenarios. It further explores practical applications with pipe flow systems, illustrating energy losses through examples of both series and parallel pipe configurations.
Detailed
In this section, the application of dimensional analysis to fluid flow is explored. The discussion begins with the concepts of velocity defects, which indicates the deviation of local velocities from the average velocity, a key aspect in characterizing turbulence. The section delves into the formulation of relationships between fluid parameters such as velocity (V), height (h), and the pipe radius (R), using experimental datasets, specifically the Nikuradse data. It introduces important equations related to energy losses in pipes, categorizing losses into major and minor types. The section also uses real-world examples of pipe flows in series and parallel arrangements, highlighting principles such as the conservation of mass and energy losses due to friction. Understanding these concepts is crucial for fluid mechanics applications, particularly in designing efficient piping systems.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Velocity Defect Concept
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
But if you go to the outer layers where we look at the velocity defect concept, how far the velocity is from the average velocity. The defect means how much deviations, how much difference between that.
Detailed Explanation
The velocity defect concept is important in fluid dynamics, particularly in analyzing how fluid flows near solid boundaries. It tells us how the speed of fluid at a certain point deviates from the average speed of the fluid. A significant velocity defect indicates that the fluid is moving slower than the average, which can affect overall flow behavior and energy transfer in a system.
Examples & Analogies
Think of this concept like a crowd of people walking in a straight line. If the average speed of the crowd is 3 miles per hour, but at one point someone is only walking at 2 miles per hour, that person represents a velocity defect – they are slower than the average, which could cause a ripple effect in the crowd's flow.
Dimensional Analysis between Velocity and Pipe Radius
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We again get the similar functions from the dimensional analysis between V and y and h. Now, if you put in a high turbulence flow and the velocity, this is called velocity defect law and h is replaced by the R, the pipe radius.
Detailed Explanation
Dimensional analysis helps us understand the relationship between various parameters in fluid dynamics. In this case, it allows us to relate the velocity (V) with the pipe diameter (R) and other factors which influence flow behavior, especially when turbulence is present. It indicates how these parameters interact, which is crucial in predicting flow characteristics.
Examples & Analogies
Imagine trying to squeeze different sizes of marbles through a narrow tube. The size of the marbles (representing radius) affects how fast they can move through the tube (representing velocity). Understanding this helps predict how changes in one affect the other.
Experimental Data from Nikuradse
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
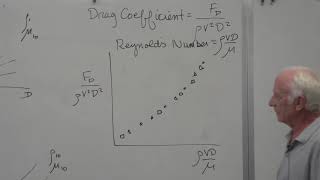
If you look at the experiment and the dimensional analysis using this Nikuradse experiment data set, it was found that the alpha value is 0.4 in the overlap zones.
Detailed Explanation
Nikuradse's experiments helped establish key relationships in fluid mechanics, particularly regarding flow in rough pipes. The alpha value of 0.4 is a significant finding that indicates how flow behaves in these zones where the characteristics change from laminar to turbulent. Understanding such values assists engineers in designing efficient piping systems.
Examples & Analogies
Think of it as testing different materials in a race. Just like how a slick surface will allow a car to go faster than a rough one, the alpha value indicates how much 'roughness' impacts the speed of fluid flow in a pipe.
Pipe Flow Examples: Series and Parallel Configurations
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at many of the times you have the pipes in series or pipes in parallel... But the total head loss is a sum of the head losses of individual pipes connected in a series.
Detailed Explanation
In plumbing or fluid systems, pipes can be arranged in series (one after another) or in parallel (side by side). In a series configuration, the total energy loss is simply the sum of the losses in each pipe. This understanding is essential for calculating system efficiency and ensuring that fluid flows correctly through a network.
Examples & Analogies
Consider a line of people passing a ball. If one person (pipe) is slow due to a poor catch, it slows down the entire line (series). In contrast, if you have multiple paths where people can pass the ball (parallel), the speed is less affected by the performance of any one person.
Energy Losses in Pipe Systems
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have a pipe in series, please remember to consider whether there are minor losses... major losses which is the frictional losses component.
Detailed Explanation
In any system of pipes, understanding both major and minor losses is essential. Major losses are typically due to friction as the fluid flows through the pipe walls, while minor losses can occur due to fittings, bends, or changes in pipe diameter. Calculating these losses is crucial in designing efficient piping systems and ensuring adequate fluid delivery.
Examples & Analogies
It's like riding your bike. The major losses can be compared to the friction between your tires and the road, while minor losses might come from the wind resistance or stops at intersections. Both need to be considered to maintain a good speed.
Key Concepts
-
Dimensional Analysis: A method to understand relationships between variables through their physical dimensions.
-
Velocity Defect: Indicates local deviations from average velocity, crucial in analyzing turbulent flows.
-
Energy Losses: Important for understanding efficiency in flow systems, involving both major and minor losses.
-
Pipe Flow: Arrangements of pipes significantly affect flow behavior and energy losses.
Examples & Applications
Example of energy loss calculations drawn from Nikuradse's experimental data, showcasing application of dimensional analysis.
Application of head loss equations in calculating energy losses for three pipes in series and parallel arrangements.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Friction's a thief, head loss in stealth, reducing flow rates, draining our wealth.
Stories
Once there was a river called Flow, who loved to speed but faced head loss woe; it learned to measure its velocity tight, through friction and turbulence, to keep it alight.
Memory Tools
Remember 'HV4E' – Head, Velocity, 4 (pipes in series), Energy losses.
Acronyms
DAVE – Dimensional Analysis for Velocity and Energy.
Flash Cards
Glossary
- Velocity Defect
The difference between the average velocity and local velocity at a specific point in the fluid flow.
- Dimensional Analysis
A method used to derive relationships between physical quantities by identifying their dimensions.
- Energy Loss
The loss of potential energy due to friction and other factors as fluid flows through a system.
- Head Loss
The reduction in total mechanical energy of the flowing fluid due to friction and other factors.
- Friction Factor
A dimensionless number used to determine the head loss due to friction in a pipe.
Reference links
Supplementary resources to enhance your learning experience.
