Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Velocity Defect Concept
Unlock Audio Lesson
Today, we will discuss the velocity defect concept in turbulent flow. Can anyone tell me what this term refers to?
Is it how much the flow velocity deviates from the average velocity?
Exactly! The velocity defect helps us understand how flow characteristics deviate from the mean, particularly in turbulence.
So, how is this measured?
Good question! It can be represented using a function of the radius of the pipe and flow characteristics. Remember, in turbulent flow, discrepancies can lead to significant energy losses.
Got it! It's essential for understanding how energy is consumed in the system.
Exactly, and understanding energy loss due to friction impacts overall efficiency in pipe systems. Let’s move on to how these losses can be calculated.
Energy Losses in Pipe Systems
Unlock Audio Lesson
When we think about energy in pipe systems, we need to consider both major and minor losses. Who can give me an example of each?
Major losses would come from friction in the pipes, right?
Yes! That’s the frictional energy loss quantified using the Darcy-Weisbach equation. And minor losses might arise from changes in pipe diameter?
Like expansion or contraction at joints!
Exactly. Both types of losses need to be factored into any flow calculations for accurate engineering analyses.
How do we combine these losses in calculations?
The total head loss in a series of pipes is the sum of all individual head losses. Always remember that!
Pipes in Series
Unlock Audio Lesson
Now, let’s apply what we learned on pipes arranged in series. What do you think happens in this configuration?
The discharge remains constant, right?
Correct! The flow rate stays constant, even though the total head loss will depend on the sum of the individual losses.
So we always need to account for both major and minor losses for each segment of the pipe?
Absolutely. Understanding this principle is critical for designing effective fluid transport systems.
And can we use similar concepts for parallel pipes?
Yes! In parallel pipes, the total head loss must be equal across all paths taken by the fluid. This is a quality we must account for in fluid dynamics!
Flow in Parallel Pipes
Unlock Audio Lesson
When we consider flow in parallel pipes, how do the flow rates distribute?
The total flow splits across the pipes, but the head losses should still equate!
Great! This split leads to a more complex calculation for individual flows. What happens when we have entry and exit losses?
We need to account for those losses in our equations. It affects the head as well.
Exactly. The concept of continuity still holds, just like in series pipes, but head loss must be solved from the perspective of each flow path.
I see, so mixing these losses while maintaining the same total discharge is key!
Perfectly put! Always remember the balance between flow and energy loss in fluid systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides insights into the velocity defect concept in turbulent flow, with a detailed look at energy losses in pipe systems due to friction. It also explores problems involving pipes in series, parallel flow configurations, and junction scenarios based on GATE 2014 questions, highlighting the application of fundamental fluid mechanics principles.
Detailed
In this section, we explore multiple aspects of pipe flow, particularly in relation to the GATE 2014 examination questions. Key points include the velocity defect and its implications for average flow speed in turbulent situations. The section emphasizes the importance of understanding both major and minor energy losses in piping systems, with distinct attention to series and parallel configurations. We elaborate on how energy is lost in frictional terms (Darcy-Weisbach friction factor) and how these losses affect flow behavior. Techniques for calculating flow rates and velocity ratios are also discussed, supported by exemplary problems reflective of academic assessments like those from GATE 2014. The practical application of these principles is crucial to ensure proper design and function of piping systems in engineering contexts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Velocity Defect Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But if you go to the outer layers where we look it that a velocity defect concept, how far the velocity from average velocity, that the defect means how much deviations how much difference between that...
Detailed Explanation
This chunk introduces the concept of velocity defect in fluid mechanics. The velocity defect refers to the difference between the average velocity of fluid flow and the local velocity at points within the flow, particularly near the boundaries like the walls of a pipe. Understanding this defect is crucial for analyzing how fluids behave under various conditions, especially in turbulent flows where velocities can fluctuate significantly.
Examples & Analogies
Think of a river. The average velocity of the river might be 2 meters per second in the center, but if you measure the velocity close to the bank, it could be much lower due to friction with the bank. The difference in speed illustrates the concept of velocity defect.
Dimensional Analysis and Experimental Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We again we get the similar functions from the dimensional analysis between V and y and h...
Detailed Explanation
This section discusses how dimensional analysis can help establish relationships between various parameters in fluid flow. It emphasizes deriving experimental correlations, particularly how velocity (V), height (h), and position (y) relate in turbulent flow. A critical factor mentioned is a constant alpha, typically denoted as 0.4, which reflects how average velocity components fluctuate, particularly during turbulent flow scenarios.
Examples & Analogies
Imagine a traffic flow where cars speed up and slow down due to traffic signals and road conditions. Dimensional analysis helps us understand how and why these speed changes occur, much like how fluid flow parameters are interconnected.
Pipe Flow and Series Connections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that, many of the times you have the pipes in series, pipes in parallel or three reservoir junction problems...
Detailed Explanation
This chunk introduces the concepts of pipes in series and parallel arrangements. When pipes are connected in series, the flow rate remains constant across all pipes, but the total head loss equals the sum of head losses in individual pipes. It's important to consider both major and minor losses due to changes in pipe diameter and fittings, which can affect overall flow efficiency.
Examples & Analogies
Consider a garden hose connected to several sprinklers in a row. The water pressure at the beginning is strong, but by the time it reaches the last sprinkler, the pressure has dropped due to friction and changing the pipe diameter—this illustrates head losses in a series configuration.
Energy Losses in Pipe Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But when you have a pipe in a series please remember it that you always should consider whether there is a minor losses...
Detailed Explanation
This section stresses the importance of accounting for both major and minor losses when calculating energy losses in pipe systems. Major losses refer to frictional losses that occur throughout the length of the pipe, while minor losses include those from fittings, valves, and diameter changes. Understanding both types of losses is essential for accurately estimating flow and pressure drop.
Examples & Analogies
Imagine riding your bike uphill. The longer and steeper the hill (analogous to major losses), the harder it is to pedal. However, if you hit bumps or potholes along the way (representing minor losses), it makes your journey even tougher, hence the different types of losses in fluid flow.
Pipes in Parallel Configuration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you have a pipe in a parallels, you can understand it see if I have the pipe in the parallels...
Detailed Explanation
In this chunk, the concept of pipes arranged in parallel is explained. When fluid flows through parallel pipes, the energy losses across all pipes must be equal, as the flow rate distributes among them. This is an essential principle when designing systems to ensure efficient fluid transport, especially in branching systems.
Examples & Analogies
Think of water flowing through multiple garden hoses laid side by side. When you turn on the faucet, the total flow is split between the hoses, but they all must deliver similar amounts of water to maintain effective watering of the plants. This concept directly mirrors the parallel flow of pipes.
Three Reservoir Junction Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we coming back to the very simple examples okay. And that is what is in your textbook...
Detailed Explanation
This section introduces the concept of a junction with three reservoirs, where fluid can flow in or out. The key focus here is the mass conservation principle, which states that the sum of inflow and outflow at the junction must equal zero. This principle is crucial for determining flow rates and pressure distributions in complex pipe systems.
Examples & Analogies
Consider a faucet with three containers (reservoirs) underneath. If the faucet is turned on, water flows into these containers. Depending on how full each container gets (the flow direction), the total water inflow will be balanced by an equivalent outflow if each container has an outlet. This illustrates how mass conservation applies in real-world scenarios.
GATE 2014 Example Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
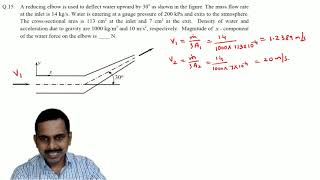
Now come back to example one which is a GATE 2014 question paper which looks like very lengthy...
Detailed Explanation
This example describes a practical problem involving two different widths of pipes leading to water flow. The problem finds the velocity ratio between the two pipe sections while considering only frictional losses, not minor losses. Key steps involve applying the Darcy-Weisbach equation to relate head losses to flow rates and velocities.
Examples & Analogies
Imagine using two different-sized straws to sip a drink. The thicker straw (larger diameter) will allow more drink to flow through it compared to a thinner straw (smaller diameter). The problem metaphorically compares pipe sizes to straw sizes and how they affect flow rates, making the mathematical relationships more relatable.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Defect: A measure of how fluid velocity deviates from the mean velocity in turbulent conditions.
-
Head Loss: Energy lost due to friction and other factors when fluid flows through a pipe.
-
Pipes in Series: Flow configuration where fluid passes through multiple segments in succession maintaining the same flow rate.
-
Pipes in Parallel: Flow configuration where fluid branches into multiple paths, requiring consideration of equal energy losses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating total head loss in a series of pipes with identified friction factors and lengths.
-
Example illustrating how energy loss calculations differ in parallel pipes with various diameters.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In pipes we see, friction is key, losses we must calculate with glee.
📖 Fascinating Stories
-
Imagine a race between two rivers—one with twists and turns, the other straight. The one with the turns loses more energy due to friction, just like water in pipes—energy loss varies!
🧠 Other Memory Gems
-
Remember 'MEP' for pipe flows: Major losses from friction, Energy losses from configurations, and Parallel systems must balance energy.
🎯 Super Acronyms
PIPE
- Piping Involves Pressure energy loss Evaluations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Defect
Definition:
The deviation of fluid velocity from its average in turbulent flow.
-
Term: Major Losses
Definition:
Energy losses primarily due to friction along the length of the pipe.
-
Term: Minor Losses
Definition:
Energy losses due to changes in pipe geometry or fittings.
-
Term: DarcyWeisbach Equation
Definition:
An equation used to calculate pressure loss due to friction in a pipe.
-
Term: Head Loss
Definition:
The loss of potential energy in a fluid system, often due to friction.
-
Term: Continuity Equation
Definition:
An expression of the principle of conservation of mass, stating that mass flow rate must remain constant.