Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Velocity Deviations
Unlock Audio Lesson
Today, we're going to talk about the Velocity Defect Concept. Can anyone tell me why understanding deviations from average velocity is important in fluid mechanics?
It's important because knowing how much the flow deviates can affect calculations for energy losses, right?
Exactly! The difference between actual and average velocity can significantly impact losses in a system, especially in turbulent flows. We call this difference the 'velocity defect.'
So, how do we measure that deviation?
Great question! We often utilize dimensional analyses that relate velocity, height, and pipe radius to quantify this. Remember, the expression for velocity defect can also help us find parameters like shear velocity.
Could you summarize the main concept about how those variables interact?
Certainly! The primary takeaway is that variations in velocity are interconnected with physical dimensions of the flow, affecting energy distribution. Thus, understanding these relationships is crucial in applications like designing piping systems.
Turbulent Flow and Velocity Defect Law
Unlock Audio Lesson
Let's delve into the velocity defect law. Who remembers the value for alpha that we derived experimentally?
Isn't it 0.4?
Correct! This alpha value represents the average velocity in turbulent flow contexts. Can anyone explain how this relates to energy losses throughout a pipe?
The energy losses will be higher with increased turbulence, right?
Exactly, and we quantify these through the Darcy-Weisbach equation. Understanding the overlap zones and logarithmic layers is key to calculating accurate energy losses!
Can you clarify what overlap zones are?
Yes! Overlap zones occur in turbulent flows where the velocity profile begins to stabilize despite fluctuating flow conditions. This zone helps define the velocity distribution more effectively.
Practical Applications in Piping
Unlock Audio Lesson
Let’s now connect our concepts to practical application. When water flows through pipes in series, what happens to the energy losses?
The total head loss is the sum of each of the pipe's head losses, right?
Spot on! This addition accounts for both major and minor losses caused by friction and changes in direction or diameter within the system. Can anyone provide a real-world example of this?
Like when water flows from tanks through pipes to a treatment facility?
Exactly! Understanding how to maintain flow despite losses is crucial in design scenarios. Driving factors include energy gradient considerations to mitigate head losses.
So we should always factor in both major and minor losses in our calculations?
Correct! Those calculations allow us to design efficient systems that can handle expected velocities and flow rates.
Analyzing Complex Flow Systems
Unlock Audio Lesson
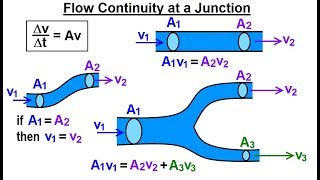
As we progress, let’s tackle flow junctions. If multiple pipes connect at a junction, how does that impact our velocity calculations?
The total discharge must equal zero at a junction, considering conservation of mass.
Excellent application of the principle! Depending on inflows and outflows, understanding energy gradients helps assess flow directions and potential loss scenarios. Why might this be pivotal in engineering?
It helps prevent issues like overflowing of tanks or inefficient systems, right?
And ensures that we meet water demands efficiently.
Exactly! The more we understand these dynamics, the more resilient our designs can be.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elaborates on the Velocity Defect Concept, explaining how the deviation of actual velocity from the average can be analyzed through dimensional analysis and defines key components in turbulent flows where experimental values determine relationships among velocity, radius, and levels of energy loss.
Detailed
Detailed Summary
The Velocity Defect Concept deals with the variations of velocity in turbulent fluid flows, particularly how actual velocities deviate from average or time-averaged velocities. This deviation is influenced by the shear velocity and the radius of the pipe through which the fluid flows. The section begins by defining the velocity defect and exploring its relationship through dimensional analysis between the velocity (V), the height (h), and the radius (r) of the pipe.
It introduces the concept of the velocity defect law and establishes how it can be experimentally derived, specifying that the parameter alpha value can be equal to 0.4 under certain flow conditions. The section also touches upon phenomena such as the logarithmic overlap layer and the effects of major and minor losses in various piping configurations, including pipes in series and pipes in parallel. To contextualize the theoretical information, practical examples are provided, illustrating how energy losses must be accounted for in fluid flow systems during calculations, especially in situations involving multiple reservoirs or junctions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Defect
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But if you go to the outer layers where we look it that a velocity defect concept, how far the velocity from average velocity, that the defect means how much deviations how much difference between that; if you look it that and looking.
Detailed Explanation
The velocity defect concept explores the difference between the instantaneous velocity of fluid particles in a flow and the average velocity of the flow. In outer layers of a flow, we observe how much the velocity deviates from this average, termed as the 'velocity defect.' This means analyzing how much individual fluid particles differ from what we define as the average behavior of the fluid.
Examples & Analogies
Imagine driving on a highway where everyone is supposed to drive at 60 mph. If one car slows down to 50 mph, that car has a velocity defect of 10 mph. Similarly, in a fluid flow, if some particles move slower or faster than the average flow speed, we can calculate their 'defect' in velocity.
Dimensional Analysis and Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We again we get the similar functions from the dimensional analysis between V and y and h.
Detailed Explanation
Dimensional analysis helps us relate different physical quantities in a fluid flow scenario. Here, we are examining how velocity (V) varies with distance (y) from the wall of the pipe and the height (h) in the flow profile. In turbulent flows, where fluid velocity fluctuates significantly, understanding these relationships aids in modeling and predicting flow behaviors.
Examples & Analogies
Think of a crowded stadium where people are moving around - how people behave (moving quickly or slowly) might depend on how close they are to the exits (h), or how much space they have (y), similar to how fluid behaves at different distances from the pipe wall.
Velocity Deflect Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it that, if you put it high turbulence flow and the velocity the reasons is very this is called velocity deflect law and h is replaced by the R the pipe radius then you can have this experimentally derived components.
Detailed Explanation
In high turbulence flows, the velocity defect law provides mathematical relationships that describe how the average velocity can be analyzed concerning turbulence intensity. The height (h) can be substituted with the pipe radius (R) in certain equations, allowing engineers to derive critical parameters for predicting flow behavior in different scenarios.
Examples & Analogies
Think of a river experiencing turbulence due to obstacles (like rocks). The 'velocity defect law' is like a rule that helps you predict how fast the water flows near the rocks compared to the calm areas, helping to understand where the fish might be hiding.
Average Velocity and Shear Velocity Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
this alpha will represent equal to the 0.4 and this is what the average velocity or time-average velocity components and this is a special average velocity component how they are fluctuating with shear velocity.
Detailed Explanation
In the context of turbulent flow, the parameter alpha represents a coefficient that quantifies the behavior of average velocity and its fluctuations in relation to shear velocity. This relationship is crucial in understanding how forces interact within the fluid layer adjacent to the pipe wall.
Examples & Analogies
Consider a special race where runners (representing average velocity) speed up and slow down due to obstacles on the track (like fluctuations caused by turbulent forces). The 'alpha' is like an average speed you calculate over several laps, accounting for those extra slow or fast moments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Defect: Indicates deviations in flow from average velocity, crucial in turbulent flow analysis.
-
Alpha Value: A unique parameter for turbulent flow indicating average velocity.
-
Dimensional Analysis: A mathematical process for comparing different physical quantities.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of head loss calculations in a series of pipes where energy loss is the sum across all pipes.
-
A practical flow scenario in a valve junction demonstrates how the total velocity and flow rates must satisfy conservation of mass.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluid flows with twists and bends, energy loss is what it spends.
📖 Fascinating Stories
-
Imagine a river flowing through rocks; sometimes it speeds up and sometimes it slows down. The spaces in between are like the velocity defects in pipes, which affect how energy is used up as it flows.
🧠 Other Memory Gems
-
V-D: Velocity Defect - Remember VO for flow velocity and DA for difference in averages.
🎯 Super Acronyms
H.E.A.D
- Head Loss
- Energy Loss
- Average Velocity
- Deviations - All important when analyzing flows.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Defect
Definition:
The difference between actual fluid velocity and average velocity in turbulent flow conditions.
-
Term: Turbulence
Definition:
A state of fluid flow characterized by chaotic changes in pressure and flow velocity.
-
Term: Dimensional Analysis
Definition:
A mathematical technique used to analyze the relationships between different physical quantities by considering their dimensions.
-
Term: Alpha Value
Definition:
A parameter that represents the average velocity in turbulent flow contexts, commonly associated with the velocity defect law.
-
Term: Logarithmic Overlap Layers
Definition:
Regions in turbulent flow where velocity profiles stabilize despite velocity fluctuations.
-
Term: Head Loss
Definition:
The loss of energy in a fluid system due to friction and other factors as it flows through pipes.
-
Term: DarcyWeisbach Equation
Definition:
An equation used to calculate head loss due to friction in a fluid flow through a pipe.
-
Term: Minor Losses
Definition:
Energy losses in fluid flow due to velocity changes or obstructions in the flow path.