Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Flexural Strength
Unlock Audio Lesson
Today, we're going to talk about flexural strength. Can anyone explain what it means?
Is it how strong the concrete is against bending?
Exactly! Flexural strength measures the ability of concrete to resist deformation under load. Now, why do you think this is important for pavements?
Because pavements need to handle heavy vehicles and pressure without cracking?
Right again! Ensuring adequate flexural strength prevents damage and prolongs pavement life. Now, the next step involves calculating the target mean flexural strength. Who wants to share how we do that?
Is it based on the characteristic flexural strength?
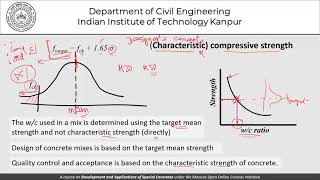
Yes! We take the characteristic flexural strength, which we denote as f_ck, and add a statistical margin. The formula is f = f_ck + k × s. Does anyone know what 'k' refers to?
Isn't it a statistical constant, like 1.65?
Good job! 'k' helps account for variability in our results. At the end of the day, why do you think this adjustment matters?
It makes sure we have a good safety margin to prevent failures?
Exactly! It’s all about ensuring the pavement can withstand real-world conditions. Let’s summarize: to find the target mean flexural strength, we use our formula with the characteristic flexural strength and the statistic constant.
Calculating Target Mean Flexural Strength
Unlock Audio Lesson
Let’s put our understanding into practice! If our f_ck is 4.5 MPa and our standard deviation is 0.6 MPa, what is our target mean flexural strength?
We plug in the numbers: f = 4.5 + 1.65 × 0.6.
Correct! What does that come out to be?
So, f = 4.5 + 0.99, which is 5.49 MPa!
Well done! That's our target mean flexural strength. Why is it important to round or consider this value carefully when designing pavement?
To ensure we meet the necessary standards for safety and durability!
Precisely! Always aim for the correct number to ensure longevity in the pavement. To conclude, the process of estimating the target mean flexural strength is vital for meeting performance expectations.
Flexural Strength’s Role in Design Criteria
Unlock Audio Lesson
Can anyone tell me how the target mean flexural strength influences other parts of our concrete mix design?
It helps determine the water-cement ratio, right?
Exactly! The right flexural strength dictates the required water-cement ratio for achieving that strength. What else may it influence?
Probably the aggregate selection and proportions dependent on that strength?
Spot on! The strength target guides us in choosing the right aggregates and ensuring their proper proportions. Does anyone have questions about why this matters in practical scenarios?
If we underestimate the strength, could the pavement fail quicker?
Absolutely! Underestimating leads to potential failures, while overestimating can cause unnecessary costs. It’s a delicate balance we must maintain.
So, verifying our calculations is super important!
Precisely! Always double-check values to ensure successful outcomes in pavement performance. Let’s summarize that flexural strength go hand-in-hand with other design criteria, reinforcing the integrity of our road systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the process of determining the target mean flexural strength required for concrete pavements. It explains how to calculate the characteristic flexural strength, incorporating statistical adjustments for variances to ensure durability and reliability in pavement applications.
Detailed
In concrete pavement design, achieving the desired flexural strength is vital for ensuring the material's performance under traffic loads and environmental factors. The section begins by discussing the calculation of the characteristic flexural strength (f_ck) and the incorporation of statistical considerations into the design process. To determine the target mean flexural strength (f), a formula is provided: f = f_ck + k × s, where 'k' is a statistical constant (typically 1.65) and 's' is the standard deviation. This method not only accounts for the inherent variability in concrete performance but also aims to meet specific design criteria ensuring that the pavement can withstand various conditions such as repeated loads and environmental stressors. The step serves as a foundational component for subsequent steps in the concrete mix design process in line with the IRC:44-2017 guidelines.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Characteristic Flexural Strength Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Determine characteristic flexural strength f ck.
Detailed Explanation
The first step in determining the mean flexural strength involves finding the characteristic flexural strength, denoted as f_ck. This value is essential as it represents the strength that the concrete is expected to achieve under standard laboratory conditions. It gives a baseline for the design, ensuring that the concrete will be strong enough for its intended use in pavement applications.
Examples & Analogies
Think of this step as setting a benchmark in sports. Just as athletes need to know their personal best (like their record time or score) to progress, engineers must know the minimum flexural strength needed to ensure that their concrete behaves as expected when put to use.
Adding a Safety Margin
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Add margin to account for variation. f = f_ck + k × s
Detailed Explanation
After determining the characteristic flexural strength, we need to account for variations in the materials and construction processes. This is done by adding a margin to the characteristic strength. The equation f = f_ck + k × s is used, where 'k' is a statistical constant (usually set at 1.65), and 's' is the standard deviation. This helps ensure that the final calculated strength (f) encompasses potential weaker sections of the concrete due to variability.
Examples & Analogies
Picture building a bridge. Engineers must account for potential unexpected stresses, much like how a bridge designer might ensure that the structure can handle heavier loads than anticipated. By using this formula, engineers create a 'buffer' to accommodate potential fluctuations in material quality and construction methods.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Flexural Strength: A crucial property that determines concrete's resistance to bending under load.
-
Characteristic Flexural Strength (f_ck): The standard measure of a concrete mix's flexural strength.
-
Target Mean Flexural Strength (f): The desired strength calculated to meet performance criteria.
-
Statistical Constant (k): A number used to adjust for variability when calculating target strength.
-
Standard Deviation (s): A statistic reflecting the variation in flexural strength measurements.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: If a concrete mix has a characteristic flexural strength of 4.5 MPa with a standard deviation of 0.6 MPa, using the formula f = f_ck + 1.65 × s results in a target mean flexural strength of 5.49 MPa.
-
Example 2: A higher target mean flexural strength indicates a potential need for a lower water-cement ratio to ensure durability and performance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flex and bend, what do we send? Ensure strength, and all will blend.
📖 Fascinating Stories
-
Imagine a bridge built on a rainy day, if the concrete lacks strength, it will surely sway!
🧠 Other Memory Gems
-
Funky Kittens Sing; for Flexural strength, k constant, and standard deviation!
🎯 Super Acronyms
FMS = Flexural Strength, Mathematical Safety!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Flexural Strength
Definition:
The ability of a material, specifically concrete, to resist deformation under load or bending.
-
Term: Characteristic Flexural Strength (f_ck)
Definition:
The standard measure that represents the flexural strength of a concrete mix.
-
Term: Target Mean Flexural Strength (f)
Definition:
The calculated flexural strength aimed for in design, considering statistical variations.
-
Term: Statistical Constant (k)
Definition:
A numerical constant (commonly 1.65) used in calculating the target mean to account for variation.
-
Term: Standard Deviation (s)
Definition:
A measure of variations or dispersion in a set of values in the context of concrete performance.