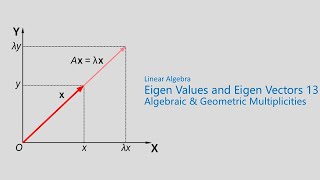
Algebraic and Geometric Multiplicities
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Algebraic and Geometric Multiplicities
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are discussing two important concepts related to eigenvalues: algebraic multiplicity and geometric multiplicity. Who can tell me what algebraic multiplicity means?

I think it’s about how many times an eigenvalue is repeated in the characteristic equation?

Exactly! Algebraic multiplicity refers to the count of how many times an eigenvalue appears as a root of the characteristic polynomial. Now, what about geometric multiplicity?

Is it the same thing?

Not quite. Geometric multiplicity refers to the dimension of the eigenspace associated with that eigenvalue, meaning the number of linearly independent eigenvectors. So, remember this relationship: the geometric multiplicity can’t exceed the algebraic multiplicity. We can think of it as 'growing roots produce only a limited number of distinct branches'.

So, if an eigenvalue has an algebraic multiplicity of 3, the geometrical multiplicity could be 1 or 2, but not more?

Precisely! That’s a great observation. The algebraic multiplicity can repeat, but the geometric multiplicity must remain less than or equal to it. Let's summarize: Algebraic multiplicity counts occurrences, whereas geometric multiplicity measures the independence of vectors. Remember this relationship as you use these concepts in real applications.
Significance of Multiplicities
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we’ve defined both types of multiplicity, let’s discuss their significance. Why do you think these multiplicities are important in engineering applications?

Maybe because they can help us understand vibration modes or structures?

Exactly! The multiplicities can characterize the behavior of systems. For example, in structural analysis, an eigenvalue with high algebraic multiplicity may indicate a critical point in a system where multiple modes could exhibit the same natural frequency.

So, does the geometric multiplicity indicate how many different ways that behavior can happen?

Correct! It tells us how many independent modes are contributing to that same frequency. The more independent modes we have, the more complex the behavior of the system can be. Can you think of a civil engineering example where these concepts apply?

In stability analysis, determining how many ways a structure can fail could relate to these multiplicities, right?

Absolutely! Different failure modes can correlate with geometric multiplicities, providing insights into the behavior of structures under different loads. A solid understanding of these terms lays the groundwork for analyzing structural integrity.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Algebraic and geometric multiplicities of eigenvalues are vital in understanding the behavior of matrices. The algebraic multiplicity refers to how many times an eigenvalue appears in the characteristic polynomial, while geometric multiplicity refers to the number of linearly independent eigenvectors associated with an eigenvalue. The relationship between the two multiplicities is a critical aspect in studying matrix properties.
Detailed
Algebraic and Geometric Multiplicities
In the context of eigenvalues, the algebraic multiplicity of an eigenvalue C6 is defined as the number of times that eigenvalue appears as a root of the characteristic polynomial of a matrix. It is an important property that helps determine the structure of the matrix. On the other hand, the geometric multiplicity measures the dimension of the eigenspace associated with that eigenvalue. This is equivalent to the number of linearly independent eigenvectors corresponding to the eigenvalue.
A crucial fact to note is the relationship between these two properties: the geometric multiplicity is always less than or equal to the algebraic multiplicity (i.e.,
1 C6 C3 Geometric Multiplicity C4 Algebraic Multiplicity). This means that while an eigenvalue can appear multiple times as a root, there may not be that many independent vectors associated with it. This section lays the foundation for exploring the properties of eigenvalues in greater depth, specifically in applications related to stability analysis and system behavior in engineering.
Youtube Videos


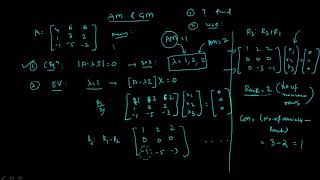



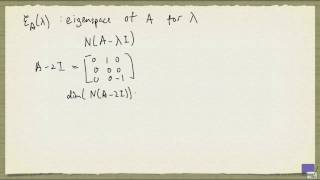

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Algebraic Multiplicity Defined
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The algebraic multiplicity of an eigenvalue λ is the number of times λ appears as a root of the characteristic polynomial.
Detailed Explanation
Algebraic multiplicity refers to how many times an eigenvalue is repeated as a solution (root) of the characteristic polynomial, which is derived from a matrix. If a specific eigenvalue appears multiple times as a root, its algebraic multiplicity is equal to that count. For instance, if the characteristic polynomial has the term (λ - 2)², then the eigenvalue λ = 2 has an algebraic multiplicity of 2.
Examples & Analogies
Think of algebraic multiplicity like the number of times a contestant wins a game show. If a contestant wins 3 times, their 'win' has an algebraic multiplicity of 3, just like an eigenvalue that appears 3 times as a root.
Geometric Multiplicity Explained
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The geometric multiplicity is the dimension of the eigenspace corresponding to λ, i.e., the number of linearly independent eigenvectors associated with λ.
Detailed Explanation
Geometric multiplicity indicates the number of linearly independent eigenvectors associated with a given eigenvalue. Each eigenvector corresponds to a direction in which the transformation detailed by the matrix can be stretched or compressed. If a specific eigenvalue has two independent eigenvectors, its geometric multiplicity is 2. This multiplicity shows how
- Chunk Title: Relationship Between Multiplicities
- Chunk Text: Important: 1 ≤ Geometric Multiplicity ≤ Algebraic Multiplicity.
- Detailed Explanation: The relationship indicates that the geometric multiplicity (the number of linearly independent eigenvectors) can never exceed the algebraic multiplicity (the total count of times an eigenvalue appears). This relationship suggests that for each eigenvalue, at least one eigenvector exists, but there could be more. Thus, the geometric multiplicity will always be at least 1 and is always less than or equal to its algebraic counterpart.
Examples & Analogies
Consider a library where one book (eigenvalue) is available in several copies (algebraic multiplicity). Each unique book layout arrangement or shelf location (geometric multiplicity) can support that book but cannot exceed the number of copies available. Hence, every book is at least one unique way to access it, but the choices can't surpass the total number of copies.
Key Concepts
-
Algebraic Multiplicity: The count of how many times an eigenvalue appears in the characteristic polynomial.
-
Geometric Multiplicity: The number of linearly independent eigenvectors associated with an eigenvalue.
Examples & Applications
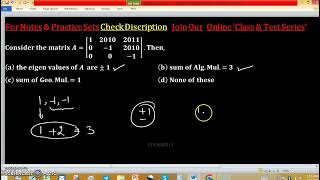
If a matrix has an eigenvalue λ = 2 with algebraic multiplicity of 3, it appears three times in the characteristic polynomial.
The corresponding geometric multiplicity might be 1 if there is only one linearly independent eigenvector associated with λ = 2.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Algebra’s count in the root parade, Geometric’s the dimension made.
Stories
Picture a garden where roots sprout higher, Algebraic counts, while Geometric inspires!
Memory Tools
For multiplicities, think 'Aunt G' and 'Uncle A'; Aunt G (geometric) is less than Uncle A (algebraic).
Acronyms
AGE
Algebraic gives the total
Geometric gives the independent.
Flash Cards
Glossary
- Algebraic multiplicity
The number of times an eigenvalue appears as a root of the characteristic polynomial.
- Geometric multiplicity
The dimension of the eigenspace corresponding to an eigenvalue, representing the number of linearly independent eigenvectors associated with that eigenvalue.
Reference links
Supplementary resources to enhance your learning experience.
