Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Complex Eigenvalues and Eigenvectors
Unlock Audio Lesson
Today, we will discuss complex eigenvalues and eigenvectors, important concepts when our matrices have complex entries. Can anyone tell me why complex numbers might be needed in our analyses?
I think it's because they can represent oscillations or waveforms that we see in dynamic systems?
Exactly, well done! Complex eigenvalues arise in systems like damped vibrations. When we have matrices with complex entries, the resulting eigenvalues can also be complex, representing these oscillatory behaviors. Now, how might this affect our computations?
Would it make our calculations more complicated?
Yes, it can. That's where understanding Hermitian matrices and unitary diagonalization comes into play. Let's dive deeper into those concepts next.
What's a Hermitian matrix?
Great question! A Hermitian matrix is similar to a symmetric matrix, but it applies to complex numbers. It has some nice properties we can utilize, such as ensuring real eigenvalues. Remember, a Hermitian matrix satisfies A = A*.
I see! So, it helps keep our eigenvalues real even though our matrix has complex parts?
Exactly! Great job summarizing that! Now let's look at the importance of unitary diagonalization.
Unitary Diagonalization
Unlock Audio Lesson
Let's discuss unitary diagonalization. Can anyone tell me what unitary matrices are?
Are they matrices that maintain orthogonality in some way?
Correct! A unitary matrix U has the property that U*U = I, where U* is the conjugate transpose, and I is the identity matrix. With unitary diagonalization, we express a complex matrix as A = UΛU*. Why do you think this is beneficial?
It sounds like it simplifies the matrix, making it easier to work with.
Exactly! This can help in things like solving systems of differential equations or analyzing complex dynamic behaviors in civil engineering applications. To summarize, can anyone recapture what we learned about complex eigenvalues and unitary diagonalization?
Complex eigenvalues are crucial for understanding oscillations, and unitary diagonalization helps us simplify computations involving complex matrices.
Great summary! This knowledge is essential for tackling more complex systems in civil engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In advanced applications like damped vibrations and electrical network modeling in civil engineering, matrices may possess complex entries. This section highlights the implications of complex eigenvalues and eigenvectors, introduces Hermitian matrices, and discusses the process of unitary diagonalization. Understanding these principles is crucial for analyzing complex systems effectively.
Detailed
Generalization to Complex Matrices and Systems
In many advanced civil engineering applications, such as damped vibration analysis and electrical network modeling, matrices can contain complex entries. This characteristic leads to the extension of the eigenvalue theory from real numbers to complex numbers.
Key Concepts
- Complex Eigenvalues: Eigenvalues can take on complex values, meaning they can be expressed in the form of a + bi, where a and b are real numbers. This situation often occurs in dynamical systems where oscillatory behavior is present, such as vibration analysis.
- Complex Eigenvectors: When eigenvalues are complex, the corresponding eigenvectors also become complex, indicating behavior that cannot be captured by real numbers alone. This is particularly important when analyzing oscillatory solutions in mechanical systems.
Important Tools in Complex Matrices
- Hermitian Matrices: These matrices serve as the complex analog of symmetric matrices in real number contexts. A Hermitian matrix satisfies the condition A = A, where A is the conjugate transpose of A. Hermitian matrices have real eigenvalues, which can be very advantageous in engineering calculations.
- Unitary Diagonalization: A complex matrix can often be diagonalized via a unitary matrix, expressed as A = UΛU*, where U is unitary and Λ is a diagonal matrix containing the eigenvalues. This diagonalization is fundamental for simplifying complex systems and making computations more tractable.
Conclusion
Understanding the implications of complex eigenvalues and eigenvectors is essential for engineering fields that deal with complex systems, enabling effective analysis and application of mathematical models.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Complex Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In some advanced civil engineering applications (e.g., damped vibrations, electrical network modeling), matrices may have complex entries. The theory of eigenvalues extends naturally to complex matrices:
- Eigenvalues can be complex.
Detailed Explanation
In certain advanced fields like civil engineering, particularly in systems dealing with damped vibrations or electrical circuit analysis, we can encounter matrices with complex numbers. Standard eigenvalue theory applies to these matrices as well. Unlike usual cases where eigenvalues are real numbers, complex matrices allow for eigenvalues to also be complex. This simply means that the eigenvalues can take on values that include imaginary parts, which is crucial for analyzing systems with oscillatory behavior.
Examples & Analogies
Think of a swing moving back and forth. In a simple scenario, we might only consider the swing's height and speed (real values). However, if we account for the forces like air resistance and how they change direction over time, we might need to describe its motion using complex numbers, capturing both the action of the swing (real parts) and the effects of damping (imaginary parts).
Complex Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Complex eigenvectors arise in oscillatory and damping solutions.
Detailed Explanation
When matrices have complex eigenvalues, their associated eigenvectors must also be complex. These complex eigenvectors are significant in scenarios where we are dealing with oscillatory systems—like electronic circuits or vibration modes of structures undergoing damping. The complex components of these eigenvectors help us understand how these systems behave over time, allowing for better modeling of their motion or energy dissipation.
Examples & Analogies
Imagine you're designing a bridge that sways slightly in the wind. The actual sway can be represented by real values—how far left or right it moves. However, if we consider how the frequency of that sway changes due to factors like wind speed or structural material, we would also consider complex numbers to accurately model that behavior. The complex eigenvectors reflect these factors as they describe how the sway evolves with time.
Hermitian Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important tools:
- Hermitian matrices (analog of symmetric matrices over complex numbers).
Detailed Explanation
Hermitian matrices are the complex counterpart to symmetric matrices, which means they possess certain properties that make them similar, though they apply in a complex number context. A matrix A is Hermitian if it is equal to its own conjugate transpose (A = A*). This property ensures that the eigenvalues of Hermitian matrices are real, making them particularly useful in physics and engineering where real-valued outcomes are essential. Thus, Hermitian matrices allow for the unfolding of complex eigenvalue phenomena while retaining the practicality of real values in solutions.
Examples & Analogies
Consider a crystal structure in materials science that can be analyzed using a specific type of matrix. If we use complex numbers to model the interactions within the crystal, we can end up with a Hermitian matrix. This matrix will let us understand how the crystal will reflect light or react to stress, while still being able to derive real outcomes about its properties from these complex representations.
Unitary Diagonalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
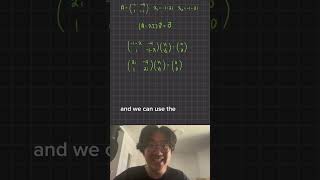
Unitary diagonalization: A=UΛU∗
Detailed Explanation
Unitary diagonalization is a technique applied to matrices with complex entries. When we have a matrix A, we can represent it as a product of a unitary matrix U, a diagonal matrix Λ containing its eigenvalues, and the conjugate transpose of U (U*). This process is analogous to diagonalization in real matrices, but it takes into account the complex nature of the entries and is an essential tool for simplifying the analysis of complex systems. This transformation makes it easier to compute functions of matrices or solve differential equations involving complex matrices.
Examples & Analogies
Imagine you're trying to solve for frequencies in a complex electrical circuit. Each component of the circuit contributes to an overall behavior represented by a complex matrix. By using unitary diagonalization, you can break down this matrix into simpler parts (like separating ingredients in a recipe) that are easier to analyze individually, but still reflect the original complex behavior when combined.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Complex Eigenvalues: Eigenvalues can take on complex values, meaning they can be expressed in the form of a + bi, where a and b are real numbers. This situation often occurs in dynamical systems where oscillatory behavior is present, such as vibration analysis.
-
Complex Eigenvectors: When eigenvalues are complex, the corresponding eigenvectors also become complex, indicating behavior that cannot be captured by real numbers alone. This is particularly important when analyzing oscillatory solutions in mechanical systems.
-
Important Tools in Complex Matrices
-
Hermitian Matrices: These matrices serve as the complex analog of symmetric matrices in real number contexts. A Hermitian matrix satisfies the condition A = A, where A is the conjugate transpose of A. Hermitian matrices have real eigenvalues, which can be very advantageous in engineering calculations.
-
Unitary Diagonalization: A complex matrix can often be diagonalized via a unitary matrix, expressed as A = UΛU*, where U is unitary and Λ is a diagonal matrix containing the eigenvalues. This diagonalization is fundamental for simplifying complex systems and making computations more tractable.
-
Conclusion
-
Understanding the implications of complex eigenvalues and eigenvectors is essential for engineering fields that deal with complex systems, enabling effective analysis and application of mathematical models.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In electrical network modeling, complex eigenvalues can represent the stability of the network when subjected to varying frequencies.
-
Damped vibrations in structures can be analyzed using complex eigenvalues and vectors to model how structures respond over time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Complex adds a twist, in vibrations it will assist.
📖 Fascinating Stories
-
Imagine a bridge swaying in the wind; the oscillations can be modeled using complex eigenvalues, turning engineering into a dance.
🧠 Other Memory Gems
-
Remember 'H-U-C' for Hermitian, Unitary, and Complex to guide you in matrix definitions.
🎯 Super Acronyms
Use 'H-CU' to remember Hermitian matrices yield real eigenvalues and Unitary diagonalization helps simplify.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Eigenvalue
Definition:
An eigenvalue that can take on complex numbers, particularly relevant in systems exhibit oscillatory behavior.
-
Term: Complex Eigenvector
Definition:
An eigenvector associated with a complex eigenvalue, demonstrating behavior involving complex solutions.
-
Term: Hermitian Matrix
Definition:
A complex matrix that is equal to its conjugate transpose, having real eigenvalues.
-
Term: Unitary Matrix
Definition:
A square matrix whose conjugate transpose is also its inverse, maintaining vector norms.
-
Term: Unitary Diagonalization
Definition:
The process of diagonalizing a complex matrix using a unitary matrix.