Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to QR Algorithm
Unlock Audio Lesson
Today, we are discussing the QR algorithm, which is a powerful numerical method for calculating eigenvalues. Can anyone tell me what eigenvalues are and why they're important?
Eigenvalues are the scalars associated with a matrix that imply how it stretches or compresses space.
Exactly! And the QR algorithm helps us find all eigenvalues of a square matrix efficiently. Does anyone know how the QR algorithm starts?
Does it involve decomposing the matrix into Q and R matrices?
Yes! The first step is to perform QR decomposition, where a matrix A is decomposed into an orthogonal matrix Q and an upper triangular matrix R.
Iterative Process of QR Algorithm
Unlock Audio Lesson
As we repeat this process, the matrix will converge to an upper triangular matrix, right?
Exactly! And the eigenvalues will be located along the diagonal of the upper triangular matrix at that point.
So this means we can directly read off the eigenvalues once the matrix is in triangular form?
Correct! This is one of the key advantages of the QR algorithm.
Applications in Civil Engineering
Unlock Audio Lesson
Can anyone think of why the QR algorithm is particularly useful in civil engineering, especially regarding vibration analysis?
It’s probably used to analyze complex structures and their modes of vibration.
Yes! The ability to find all eigenvalues means we can determine the natural frequencies of structures, which is critical for ensuring stability.
What about non-symmetric matrices? Can this algorithm still be used?
Great question! Yes, the QR algorithm can be applied to any square matrix, although it converges faster for symmetric matrices due to their inherent properties.
Advantages and Limitations of QR Algorithm
Unlock Audio Lesson
What are some advantages of using the QR algorithm compared to other eigenvalue computation methods?
It’s applicable to a wider range of matrices and converges faster for symmetric matrices.
Exactly! However, can anyone think of any limitations?
Maybe it can be computationally intensive for very large matrices?
Correct! It can be less efficient for extremely large matrices compared to methods like the power method.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the QR algorithm, a robust method for calculating eigenvalues of matrices. It involves QR decomposition, iterating the matrix until it converges to an upper triangular matrix with eigenvalues on the diagonal. This method is applicable to general square matrices and offers faster convergence for symmetric matrices, making it essential in fields such as civil engineering.
Detailed
The QR algorithm is a powerful method for computing eigenvalues (and optionally eigenvectors) of square matrices. The basic procedure starts with a square matrix A, which can be broken down into an orthogonal matrix Q and an upper triangular matrix R through QR decomposition. The algorithm iterates on the matrix such that A_k = Q_k^T * A_k-1 * Q_k, refining it over time. As the iterations progress, the resulting matrix approaches an upper triangular form with the eigenvalues appearing on the diagonal. This method is particularly advantageous in that it applies to a broad range of square matrices and has faster convergence for symmetric ones, making it especially useful in engineering applications like vibration analysis.
Youtube Videos
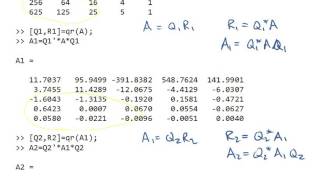
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Idea of the QR Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The QR algorithm is a robust numerical method to compute all eigenvalues (and optionally eigenvectors) of a square matrix.
If A = A₀, then:
A₀ = QR, A₁ = RQ
Where:
• Q is orthogonal, R is upper triangular (via QR decomposition),
• This process iterates: Aₖ₊₁ = QᵀAₖQ.
As k → ∞, A converges to an upper triangular matrix with eigenvalues of A on the diagonal.
Detailed Explanation
The QR algorithm aims to find the eigenvalues of a matrix through a repeated process. Initially, you take a square matrix A and decompose it into two matrices, Q (an orthogonal matrix) and R (an upper triangular matrix) such that A = QR. Next, you rearrange these matrices and construct a new matrix A₁ by calculating A₁ = RQ. This reconfiguration is iterated multiple times: A₂ = QA₁Q, and so forth. After many iterations, the matrix A converges to an upper triangular form, where the diagonal elements represent the eigenvalues of the original matrix A. Essentially, you are transforming the matrix while preserving its eigenvalues until they become apparent on the diagonal of the final result.
Examples & Analogies
Imagine you’re trying to figure out the tallest buildings in a city. Instead of measuring each building directly, you take photos from above, sort the images based on their heights in each iteration, and then refine your approach. Eventually, you’ll see the buildings organized neatly by height, similar to how the QR algorithm reveals eigenvalues one by one through refinements.
Advantages of the QR Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Advantages:
• Applicable to general square matrices.
• Works well with symmetric matrices (faster convergence).
Detailed Explanation
The QR algorithm has significant advantages in numerical computations. First, it can be applied to any square matrix, making it versatile. This broad applicability means it can handle most problems involving matrices we encounter in engineering or scientific applications. Moreover, when dealing with symmetric matrices—those equal to their transpose—the QR algorithm becomes even more efficient, ensuring faster convergence to the correct eigenvalues. This is beneficial in fields like civil engineering, where symmetric matrices often arise in analysis.
Examples & Analogies
Think of the QR algorithm like a universal tool kit—it can address a variety of tasks (general square matrices) and is a specialized tool for precise jobs (symmetric matrices) that allows you to work more efficiently.
Civil Engineering Use of the QR Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Civil Engineering Use:
Used in vibration analysis software to compute full mode shapes of complex structural systems.
Detailed Explanation
In civil engineering, the QR algorithm plays a crucial role, particularly in software used for vibration analysis of structures, such as buildings and bridges. Engineers model these structures to predict how they will respond to various forces or vibrations. To ensure safety and design efficiency, they need to compute the full mode shapes—these are essentially the patterns of vibration that can occur in the structure. The QR algorithm helps extract these mode shapes by finding the eigenvalues and eigenvectors associated with the stiffness and mass matrices, allowing engineers to ascertain critical information about the behavior of the structure.
Examples & Analogies
Imagine a bridge swaying in the wind. Just like how musicians tune instruments to find the right frequencies to play music harmoniously, engineers use the QR algorithm to find the 'frequencies' at which a bridge may vibrate during wind events or earthquakes to ensure it remains safe and stable.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
QR Algorithm: A robust numerical method to compute all eigenvalues of a matrix.
-
QR Decomposition: Process that expresses a matrix in terms of an orthogonal matrix and an upper triangular matrix.
-
Convergence: The iterative process approaches an upper triangular form with eigenvalues on the diagonal.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the QR algorithm, you can compute eigenvalues for large structural matrices in engineering applications, enhancing stability analysis.
-
If a matrix A can be decomposed into Q and R such that A = Q * R, we can iteratively refine this to find eigenvalues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When Q and R you see, eigenvalues will soon be!
📖 Fascinating Stories
-
Imagine a matrix taking a journey—first it dresses in Q (orthogonal) and then structures itself as R (upper triangular) before revealing its eigenvalues.
🧠 Other Memory Gems
-
Remember QR in the chase: Q for Quick (orthogonal) and R for Right (upper triangular).
🎯 Super Acronyms
QRE - 'Quickly Reveal Eigenvalues'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: QR Algorithm
Definition:
A numerical method used to compute all eigenvalues and eigenvectors of a square matrix.
-
Term: QR Decomposition
Definition:
The process of decomposing a matrix into an orthogonal matrix Q and an upper triangular matrix R.
-
Term: Eigenvalue
Definition:
A scalar value that characterizes the scaling factor of eigenvectors under the transformation of a matrix.
-
Term: Upper Triangular Matrix
Definition:
A matrix where all the entries below the main diagonal are zero.
-
Term: Convergence
Definition:
The process of approaching a limit or a final state as iterations increase.