Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Eigenvalues and Eigenvectors
Unlock Audio Lesson
Good morning class! Today we’re going to discuss eigenvalues and eigenvectors. To start off, can anyone tell me what they think an eigenvalue is?
Isn't it a special number associated with a matrix?
Yes, exactly! An eigenvalue is a scalar λ associated with a matrix A, which satisfies the equation Ax = λx for some non-zero vector x. What do we call this vector?
That would be the eigenvector, right?
Exactly! The eigenvector is non-zero and it gives us important insights into the matrix's properties. To remember this, think of the phrase: 'Eigen, like the eigenvalue, finds its partner.'
What happens if we rearrange the equation?
Great question! We can express it as (A - λI)x = 0. This is important because it leads us to the characteristic equation. Can anyone remind me what we do with this equation?
We calculate the determinant to find λ?
That's right! The determinant det(A - λI) must equal zero for non-trivial solutions. So, in summary, eigenvalues and eigenvectors help us transform linear systems effectively.
Characteristics of Eigenvalues
Unlock Audio Lesson
Now let’s explore how we compute eigenvalues. What’s the first step?
Start with our square matrix A.
Correct! Next, what do we subtract from A?
We subtract λI, right?
Exactly! So we have A - λI. After that, we find the determinant. What does setting this equal to zero tell us?
It tells us about the eigenvalues from the characteristic polynomial!
Exactly! And remember, the characteristic polynomial is pivotal to understanding the behavior of our matrix. What can you tell me about the solutions we find?
There are both algebraic and geometric multiplicities for the eigenvalues?
Yes! Algebraic tells us how many times a value appears as a root, whereas geometric tells us the dimension of the associated eigenspace. A quick way to recall this: Every root has a corresponding space!
What do we do after finding the eigenvalues?
We substitute each eigenvalue into the equation to solve for the corresponding eigenvectors! Together, they help us understand the matrix's properties better. Any questions before we proceed?
Applications in Engineering
Unlock Audio Lesson
Okay class, let’s discuss the applications of what we've just learned. In civil engineering, where do you think we might apply eigenvalues?
Could it be for analyzing vibrations in structures?
Correct! Eigenvalues can indicate natural frequencies in structures - higher eigenvalues correspond to stiffer modes. How about stability?
Are they used in buckling analysis too?
Yes! In such cases, we deal with problems like (K - λG)x = 0, where eigenvalues lead to critical loads. Excellent connection! Lastly, how do they help in stress analysis?
The eigenvalues indicate principal stresses in the stress tensor, right?
Exactly! Understanding these applications helps frame our analysis in real-world situations. Remember: 'Eigenvalues provide insights into vibrations, shapes, and stability in structures!'
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section defines eigenvalues and eigenvectors in the context of square matrices, explaining that an eigenvalue can be identified with a non-zero vector that transforms linearly. It lays the groundwork for understanding how these concepts are essential for applications in engineering, emphasizing the determinant's role in deriving the characteristic equation.
Detailed
Eigenvalues and Eigenvectors
Introduction
This section delves into the concepts of eigenvalues and eigenvectors, crucial tools for analyzing matrices in civil engineering applications. It begins with the definition of an eigenvalue, denoting it as a scalar λ that satisfies the equation Ax = λx, where A is an n×n matrix and x is a non-zero vector known as the eigenvector. The importance of these concepts stems from their application in structural stability, vibration analysis, and solutions to differential equations, which are often represented in matrix form.
Eigenvalue Equation
The equation can also be expressed as (A - λI)x = 0, leading us to the characteristic equation: det(A - λI) = 0. This equation is pivotal, as it helps find the eigenvalues of matrix A.
Characteristics
The ability of the matrix to have a non-trivial solution is tied to the singularity of the coefficient matrix, dictating the eigenvalues’ existence. The following sections will explore how to compute eigenvalues and eigenvectors, including methods for determining algebraic and geometric multiplicities, crucial in various engineering applications.
Youtube Videos
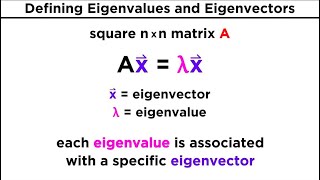
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A be an n×n square matrix. A scalar λ is called an eigenvalue of A if there exists a non-zero vector x∈Rn such that:
Ax=λx
Here:
• λ∈R (or C) is an eigenvalue,
• x is a corresponding eigenvector.
Detailed Explanation
This chunk introduces the concept of eigenvalues and eigenvectors. An eigenvalue (λ) is a special kind of scalar associated with a matrix (A). When applied to a vector (x), the matrix transforms this vector into another vector that is simply a scaled version of the original vector by λ. This relationship is expressed by the equation Ax = λx, which shows that the action of matrix A on the vector x yields a vector that retains the same direction but may change in magnitude, depending on the eigenvalue.
Examples & Analogies
Imagine you are pushing a toy car in a straight line. If you push it slightly harder, the car moves faster in the same direction (analogous to 'stretching'). If you push it less hard, it moves slower (analogous to 'compressing'). In this analogy, the direction in which the car moves is like the eigenvector, while how much faster or slower the car moves represents the eigenvalue.
Homogeneous System of Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This equation can be rearranged as:
(A−λI)x=0
This is a homogeneous system of linear equations. For a non-trivial solution (x̸=0), the coefficient matrix must be singular, i.e.,
det(A−λI)=0.
Detailed Explanation
To find the eigenvalues, we rearrange the initial equation into a form that sets up a system of linear equations: (A−λI)x = 0. This system is termed 'homogeneous' because it equals zero. For there to be a solution where x is not zero (non-trivial), the determinant of the matrix (A−λI) must equal zero, indicating that this matrix is 'singular' and lacks an inverse, which leads us to the characteristic polynomial of the matrix.
Examples & Analogies
Consider a tightrope walker trying to balance on a thin wire. If the wire is perfectly straight (analogous to the matrix being non-singular), the walker cannot find a point to position himself where he is balanced (non-zero solution). However, if the wire dips or is off-balance (the matrix becomes singular), there are multiple points where the walker can balance himself without falling, indicating multiple solutions exist.
Characteristic Equation and Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is called the characteristic equation, and the polynomial det(A−λI) is the characteristic polynomial.
Detailed Explanation
The equation det(A−λI) = 0 gives us a polynomial known as the characteristic polynomial. By solving this polynomial equation for λ, we find the eigenvalues of the matrix A. The roots of this polynomial correspond to the eigenvalues. Each eigenvalue thus gives us crucial information about how the matrix A operates on space, particularly how it stretches or compresses it in different directions.
Examples & Analogies
Imagine you have a rubber sheet that can be stretched or compressed when pulling on its corners. Each point on the surface represents a vector, and the way the sheet behaves under pressure relates to the eigenvalues. When the sheet is pulled in certain ways (the characteristic polynomial), we can understand how far and in what direction different areas of the sheet will stretch or compress.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: A scalar λ satisfying the eigenvalue equation.
-
Eigenvector: A non-zero vector associated with an eigenvalue and matrix.
-
Characteristic equation: The determinant condition used to find eigenvalues.
-
Algebraic multiplicity: Indicates how many times an eigenvalue appears as a root.
-
Geometric multiplicity: Indicates the number of linearly independent eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a 2x2 matrix where the eigenvalues and eigenvectors can be computed easily.
-
Use of eigenvalues in structural analysis to determine the natural frequencies of a building.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalue, eigenvector, partner in sync, transform with ease, don’t you think?
📖 Fascinating Stories
-
Once in Mathland, the Matrix invited Eigenvalue and Eigenvector to dance. When they did, they transformed the whole room without losing their shape, showing the power of their relationship.
🧠 Other Memory Gems
-
A quick way to remember the steps to find eigenvalues: 'A Minus Lambda I, Determine, Set to Zero.'
🎯 Super Acronyms
EVE
- Eigenvalue
- Vector
- Equation – the three elements in the eigenvalue realm.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ associated with a matrix A, satisfying the equation Ax = λx for some non-zero vector x.
-
Term: Eigenvector
Definition:
A non-zero vector x that transforms under a matrix A according to the eigenvalue equation.
-
Term: Characteristic equation
Definition:
The equation det(A - λI) = 0 whose roots are the eigenvalues of the matrix A.
-
Term: Algebraic multiplicity
Definition:
The number of times an eigenvalue appears as a root of the characteristic polynomial.
-
Term: Geometric multiplicity
Definition:
The dimension of the eigenspace associated with an eigenvalue, indicating the number of linearly independent eigenvectors.