Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Multiplicities
Unlock Audio Lesson
Today, we’ll dive into the concepts of multiplicities, specifically geometric multiplicity. First, can anyone remind me what we mean by eigenvalues and eigenvectors?
Eigenvalues are scalars that stretch vectors, and eigenvectors are the vectors that get stretched by the eigenvalue!
Exactly! Now, when we think about the multiplicity of an eigenvalue, we have two key terms: algebraic and geometric multiplicities. Let's start with algebraic multiplicity. What do you think that is?
Is it how many times an eigenvalue appears in the characteristic polynomial?
Precisely! It tells us the number of times the eigenvalue appears as a root. Now, what about geometric multiplicity? Any ideas?
I think it has to do with the number of different eigenvectors for that eigenvalue?
Spot on! Geometric multiplicity shows us the dimension of the eigenspace associated with an eigenvalue, which is the number of linearly independent eigenvectors we can have. What is the relationship between these two multiplicities?
Geometric multiplicity is always less than or equal to algebraic multiplicity!
Great summary! To visualize this, think of algebraic multiplicity as a full set of vectors, while geometric multiplicity shows how many of those vectors can be constructed independently in one direction. Let’s proceed to real-world applications next.
Applications of Multiplicities in Engineering
Unlock Audio Lesson
Multiplicities play a crucial role in fields like civil engineering, especially those involving stability analysis or vibration problems. How do you think understanding geometric multiplicity could help in these applications?
It might affect how we model structures and predict their behavior under loads.
Exactly! If the geometric multiplicity indicates there's more than one way a structure can vibrate, we need to account for those behaviors in our designs. Can anyone give me an example of where this might apply?
In the design of a bridge? It has to support multiple loads and conditions!
Yes! And the eigenvectors could represent different modes of vibration for the bridge under various conditions, which is essential for safety. How about relating this back to the conditions of multiplicity? Why is it vital that geometrical does not exceed algebraic?
If geometric is more than algebraic, it could mean that we're trying to represent more independent behaviors than the eigenvalue allows for?
Well put! Overstepping this could lead to incorrect results in engineering calculations. Remember, these multiplicities guide our understanding of how different structures will respond in defined situations.
Computational Techniques for Finding Multiplicities
Unlock Audio Lesson
Now that we understand the significance of multiplicities, let’s discuss how to calculate them. Who can tell me the first step to find the eigenvalues?
You need the characteristic polynomial, right? By calculating the determinant of A - λI.
Correct! Once we find the eigenvalues from the polynomial, how do we determine the geometric multiplicity?
By finding the null space of A - λI, right?
Right again! The dimension of that null space gives us the geometric multiplicity. It’s essential not just to find these values but also to understand their implications. Can anyone outline key points we keep in mind while solving for these?
The relationship between algebraic and geometric, and their application in engineering contexts!
Absolutely! Understanding this helps us ensure accurate modeling and analysis of structural behavior. As we continue, it’s essential to keep these ideas central to our engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Geometric multiplicity is the number of linearly independent eigenvectors for a specific eigenvalue. It is essential for understanding the behavior of matrices and how they can be diagonalized, especially in real-world applications like structural analysis. The geometric multiplicity must always be less than or equal to its algebraic multiplicity, defined as the number of times an eigenvalue appears as a root of the characteristic polynomial.
Detailed
In matrix theory, geometric multiplicity provides critical insights into the nature of eigenvalues and eigenvectors. Specifically, for a given eigenvalue λ of a matrix A, the geometric multiplicity is defined as the dimension of the eigenspace associated with λ, quantifying the degree of freedom to construct eigenvectors corresponding to that eigenvalue. This dimension is represented by the number of linearly independent eigenvectors associated with λ. Notably, it always satisfies the inequality 1 ≤ Geometric Multiplicity ≤ Algebraic Multiplicity, where algebraic multiplicity refers to the number of times λ appears as a root of the characteristic polynomial of the matrix. Understanding both geometric and algebraic multiplicities is vital, particularly in contexts such as diagonalization and stability analysis in engineering applications, where the multiplicities affect the behavior of differential systems.
Youtube Videos
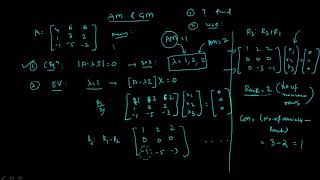
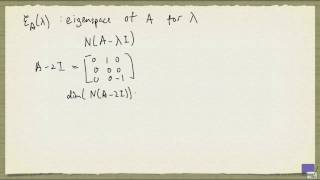
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Geometric Multiplicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The geometric multiplicity is the dimension of the eigenspace corresponding to λ, i.e., the number of linearly independent eigenvectors associated with λ.
Detailed Explanation
Geometric multiplicity measures how many unique directions (eigenvectors) exist for a specific eigenvalue (λ). Each eigenvector points in a direction where the transformation represented by the matrix only stretches or shrinks the vector, without changing its direction. The dimension of the eigenspace, associated with an eigenvalue, is defined by how many independent eigenvectors can be formed. If there are multiple eigenvectors for a single eigenvalue, it shows the complexity of the behavior of the system described by the matrix.
Examples & Analogies
Imagine a flat piece of paper (the matrix) that can stretch in multiple directions. If you have a rubber band made of the same paper that's twisted in several ways, certain points (eigenvectors) will stretch more than just one direction (eigenvalue). The number of unique ways you can stretch it without duplicating the paths gives you a sense of how many different stable positions (geometric multiplicity) the rubber band can take.
Geometric vs Algebraic Multiplicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important: 1 ≤ Geometric Multiplicity ≤ Algebraic Multiplicity.
Detailed Explanation
This important inequality means that the geometric multiplicity of an eigenvalue can never exceed its algebraic multiplicity. The algebraic multiplicity reflects how many times an eigenvalue appears in the characteristic polynomial as a root. If an eigenvalue appears several times, it could either lead to one unique eigenvector (geometric multiplicity of 1) or multiple unique eigenvectors. Thus, while we may have multiple occurrences of an eigenvalue, the actual number of independent directions it can stretch will be limited by how many unique vectors can be formed from it.
Examples & Analogies
Consider a person who can play multiple instruments but only one of them well. The total number of instruments they can play represents the algebraic multiplicity, while the one they master represents the geometric multiplicity. Hence, they may own multiple instruments, but can only showcase their 'talent' in one area.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Algebraic Multiplicity: Refers to the number of times an eigenvalue appears as a root in the characteristic polynomial.
-
Geometric Multiplicity: The number of linearly independent eigenvectors corresponding to an eigenvalue, indicating its dimensionality in eigenspace.
-
Eigenvalue Relationship: Geometric multiplicity is always less than or equal to algebraic multiplicity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: For a matrix A, if λ = 3 is an eigenvalue with algebraic multiplicity 3, and there are 2 linearly independent eigenvectors, the geometric multiplicity is 2.
-
Example 2: In a 2x2 matrix with eigenvalues λ1 = 2 and λ2 = 2, if both eigenvalues share one eigenvector, the algebraic multiplicity is 2, but the geometric multiplicity is 1.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the space where vectors thrive, geometric multiplicity keeps them alive.
📖 Fascinating Stories
-
Imagine a town where each house can only fit a certain number of cars. The algebraic multiplicity is the total number of cars (roots), while geometric multiplicity is the number of separate garages (dimensions) available.
🧠 Other Memory Gems
-
A for Algebraic, G for Geometric, and D for Dimension — remember AGD if you need multiplication.
🎯 Super Acronyms
GAM
- Geometric represents Algebric Multiplicity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ such that Ax = λx for a non-zero vector x, where A is a matrix.
-
Term: Eigenvector
Definition:
A non-zero vector x that satisfies the equation Ax = λx.
-
Term: Algebraic Multiplicity
Definition:
The number of times an eigenvalue appears as a root of the characteristic polynomial.
-
Term: Geometric Multiplicity
Definition:
The dimension of the eigenspace associated with an eigenvalue, representing the number of linearly independent eigenvectors.
-
Term: Characteristic Polynomial
Definition:
A polynomial whose roots are the eigenvalues of a matrix.
-
Term: Eigenspace
Definition:
The set of all eigenvectors corresponding to an eigenvalue, including the zero vector.