Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Concept of Eigenvalues
Unlock Audio Lesson
Today, we are going to explore how to find the eigenvalues of a square matrix. Who can remind me what an eigenvalue is?
An eigenvalue is a scalar that describes how a linear transformation changes the vectors in a vector space!
Exactly! Eigenvalues help us understand types of transformations. Now, why are we interested in finding them?
I think they're important in stability analysis in engineering!
Correct! Now let's discuss our first step in finding eigenvalues.
Start with the Square Matrix
Unlock Audio Lesson
To begin, we need a square matrix \(A\). Can someone explain why we specifically need a square matrix?
Because only square matrices have eigenvalues! Non-square matrices do not have a well-defined eigenvector equation.
Right! Now, let's move to our next step, which requires subtracting \(\lambda I\) from \(A\). What does this mean?
We use the identity matrix \(I\) multiplied by the scalar eigenvalue \(\lambda\) to establish a system!
Computing the Determinant and Characteristic Polynomial
Unlock Audio Lesson
After forming the expression \(A - \lambda I\), we compute the determinant. Can anyone tell me why computing the determinant is crucial?
The determinant tells us if the matrix is singular or non-singular, and we need it to form the characteristic polynomial.
Exactly! The result gives us a polynomial we can set to zero, which leads us directly to our eigenvalues. How do we find the roots of this polynomial?
By solving the equation \(p(\lambda) = 0\)!
Final Steps to Identify Eigenvalues
Unlock Audio Lesson
Now let's summarize our final step. Once we have the characteristic polynomial, we need to find its roots to identify the eigenvalues. Who can summarize our process?
We start with a matrix, subtract the identity times \(\lambda\), find the determinant, and then solve for the eigenvalues!
Perfect summary! Keep practicing this process because it is crucial in applications, especially in engineering!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section presents a systematic approach to computing eigenvalues from a square matrix by utilizing the characteristic polynomial. Key steps include determining the matrix, subtracting a scalar multiple of the identity matrix, solving the resulting determinant equation, and identifying the eigenvalues.
Detailed
Steps to Find Eigenvalues
In this section, we delve into a systematic approach to derive the eigenvalues of a square matrix, which plays a pivotal role in various applications of linear algebra, particularly in the fields of civil engineering and applied mathematics. The steps to compute eigenvalues from a given square matrix \(A\) are as follows:
- Start with the square matrix \(A\): Begin with the matrix whose eigenvalues you wish to compute.
- Subtract \(\lambda I\) from \(A\): Formulate the expression \(A - \lambda I\), where \(I\) is the identity matrix of the same dimension as \(A\) and \(\lambda\) is a scalar.
- Compute the determinant \(det(A - \lambda I)\): This step involves calculating the determinant of the matrix \(A - \lambda I\). The result gives rise to a polynomial equation known as the characteristic polynomial.
- Solve the characteristic polynomial \(p(\lambda) = 0\): By finding the roots of the characteristic polynomial, you obtain the eigenvalues of the matrix. These eigenvalues are critical in assessing the properties and behaviors of the linear transformations represented by the matrix \(A\).
Youtube Videos
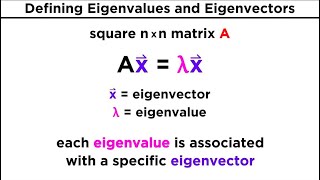
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Starting Point
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Start with the square matrix A.
Detailed Explanation
This step requires you to have a square matrix, which means that the number of rows is equal to the number of columns. Eigenvalue calculations apply specifically to square matrices, as they preserve the dimensional properties necessary for analysis. To find eigenvalues, you must begin with a clearly defined square matrix, denoted here as A.
Examples & Analogies
Think of a square matrix like a building with a specific structure, where each story (row) has the same number of rooms (columns). To understand the building's design better (the mathematics), you need to clearly define its layout (the square matrix).
Subtracting λI
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Subtract λI from A to get A−λI.
Detailed Explanation
In this step, 'λ' represents a scalar, which is treated as a variable during calculations. 'I' is the identity matrix, which has ones on the diagonal and zeros elsewhere. When you subtract λI from A, you essentially create a new matrix (A−λI) that helps to determine the eigenvalues. This operation aligns the dimensions of A and λI, ensuring they can be subtracted correctly.
Examples & Analogies
Imagine adjusting the height of each floor in our building by a specific amount (λ) that is constant. What we're doing is modifying the original dimensions to see how these changes affect the overall structure when analyzing stability or design.
Calculating the Determinant
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Compute the determinant det(A−λI).
Detailed Explanation
The determinant of the matrix (A−λI) is a scalar value that provides critical information regarding the properties of that matrix. Specifically, if the determinant equals zero, it indicates that the matrix is singular, which implies there are non-trivial solutions (non-zero vectors). This is essential for finding eigenvalues, as they are solutions to the characteristic polynomial derived from this determinant.
Examples & Analogies
Consider the determinant as a measure of how well the structure can support weight. A determinant of zero suggests that the building is unstable and cannot hold any load without collapsing, similar to how eigenvalues represent points of instability in a mathematical model.
Solving the Characteristic Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Solve the resulting characteristic polynomial p(λ)=0 for λ. These are the eigenvalues.
Detailed Explanation
After calculating the determinant, you'll arrive at a polynomial equation in terms of λ, known as the characteristic polynomial. To find the eigenvalues, you set this polynomial equal to zero (p(λ)=0) and solve for λ. The solutions to this equation provide the eigenvalues of the original matrix A.
Examples & Analogies
This step can be likened to solving a puzzle where you have to find specific pieces (the eigenvalues) that fit into the overall picture of your structure (the matrix). Each eigenvalue helps in understanding how the system behaves under certain conditions, just like each puzzle piece contributes to the final image.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Square Matrix: A matrix with an equal number of rows and columns necessary for the existence of eigenvalues.
-
Characteristic Polynomial: The polynomial derived from the determinant \(det(A - \lambda I) = 0\).
-
Eigenvalues: Solutions to the characteristic polynomial equation that represent scalar transformations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given a matrix \(A = \begin{bmatrix} 4 & 1 \ 1 & 4 \end{bmatrix}\), the eigenvalues can be found by calculating \(det(A - \lambda I) = 0\) where \(I\) is the identity matrix.
-
For the matrix \(B = \begin{bmatrix} 1 & 2 \ 0 & 1 \end{bmatrix}\), find eigenvalues through the determinant calculation of \(det(B - \lambda I) = 0\) leading to its characteristic equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find lambda, don't forget, subtract identity, stay on set!
📖 Fascinating Stories
-
Once there was a matrix, strong and square. To find its magical lambda, we had to pair it with an identity, take a step, find its determinant’s fate!
🧠 Other Memory Gems
-
Silly Cats Dance: Steps to remember: Start with the matrix ➔ Subtract \(\lambda I\) ➔ Determine ➔ Set to zero.
🎯 Super Acronyms
E.V.D.P
- Eigenvalues - Find the Determinant - Polynomial = zero.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar \(\lambda\) for which there exists a non-zero vector \(x\) such that \(Ax = \lambda x\).
-
Term: Eigenvector
Definition:
A non-zero vector that satisfies the equation \(Ax = \lambda x\) for a given eigenvalue \(\lambda\).
-
Term: Determinant
Definition:
A scalar value that is a function of a square matrix, providing a measure of the matrix's singularity.
-
Term: Characteristic Polynomial
Definition:
A polynomial obtained from the determinant equation \(det(A - \lambda I) = 0\).