Eigenvalues
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues and Eigenvectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll discuss eigenvalues and eigenvectors, which are crucial in analyzing matrices related to structural engineering. Can anyone explain what an eigenvalue is?

An eigenvalue is a scalar value that indicates how much the eigenvector is stretched or shrunk when transformed by the matrix.

Exactly! An eigenvalue λ has a corresponding eigenvector x, satisfying the equation Ax = λx. This relationship is key for understanding transformations.

And how do we find these eigenvalues?

Great question! We can find eigenvalues using the characteristic equation, which stems from det(A - λI) = 0. Remember, 'det' refers to the determinant.

So we rearrange the matrix A with λI, and solve for λ?

Correct! And once we find λ, we can substitute it back to find the corresponding eigenvectors. Have you all heard of these concepts before?

Yes, but I didn’t know how they were applied in engineering!

These concepts have vital applications in stability analysis of structures and understanding vibrations. Let's summarize: eigenvalues help tell us how matrices function under certain transformations.
Computing Eigenvalues and Eigenvectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's delve into how we can compute eigenvalues and eigenvectors. What are the first steps?

We start with the matrix A and subtract λI to form A - λI.

Great! Then what do we do with that?

Next, we calculate the determinant of A - λI and set it to zero.

Right! If we find the roots of the resulting polynomial, we get the eigenvalues. What's next after that?

We take each eigenvalue and substitute it back into the equation to solve for the corresponding eigenvector!

Exactly! Let’s summarize today's key point: finding eigenvalues involves working with determinants forming characteristic polynomials, followed by substituting back to determine eigenvectors.
Properties of Eigenvalues
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss some properties of eigenvalues. Can anyone share how eigenvalues relate to the trace and determinant of a matrix?

The sum of the eigenvalues equals the trace of the matrix, and the product equals the determinant!

Correct! This is a powerful tool for understanding matrix characteristics. What about the properties of triangular matrices?

Their eigenvalues are the entries on the diagonal!

Absolutely! Now, let's discuss symmetric matrices. What notable feature do they possess regarding eigenvalues?

They have real eigenvalues and are orthogonally diagonalizable!

Great summary! Understanding these properties allows us to analyze matrices more effectively in engineering applications like structural stability.
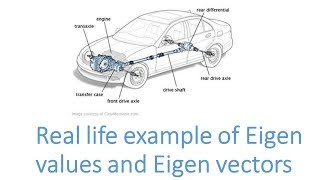
Applications of Eigenvalues in Civil Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's transition to practical applications. How are eigenvalues used in structural analysis?

They represent the natural frequencies of structures.

Exactly! A large eigenvalue indicates a stiff mode, while a small one indicates flexibility. Can anyone give an example?

In stability analysis, eigenvalues can help predict buckling behavior.

Correct! The equation (K - λG)x = 0 is often used here. What else can you think of?

Eigenvalues also help in modal analysis of buildings and bridges during vibrations.

Great point! So, we see that applying theoretical knowledge to real-world problems enhances our ability to design safe structures. Let’s summarize: eigenvalues are pivotal in structural analysis, stability, and damage assessment.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Eigenvalues and eigenvectors play crucial roles in various civil engineering applications, such as stability analysis and modal analysis. The underlying concepts are explored, including definitions, methods for computation, and key properties. These tools are vital for understanding linear transformations applied to engineering scenarios.
Detailed
Eigenvalues in Context
Eigenvalues and eigenvectors are essential mathematical tools in civil engineering, primarily dealing with matrices that relate to structural stability and vibration analysis. In this section, we define eigenvalues and eigenvectors, illustrating their importance to linear transformations where vectors are stretched, compressed, or rotated.
Definitions and Concepts
The section begins by defining eigenvalues (λ) and eigenvectors (x) in relation to a square matrix (A). It also introduces the characteristic equation, emphasizing the significance of determinants in determining eigenvalues.
Computing Eigenvalues and Eigenvectors
We detail the steps for computing eigenvalues and corresponding eigenvectors, providing structured guidance on solving the characteristic polynomial. Understanding both algebraic and geometric multiplicities of eigenvalues further aids in grasping the behavior of matrices.
Properties of Eigenvalues
This portion elucidates important properties such as the relationship between trace, determinant, and eigenvalues, and highlights characteristics unique to symmetric matrices. Each property has practical implications for civil engineering applications, where analyzation of structures is prevalent.
Applications
Lastly, the applications of eigenvalues in civil engineering are explored, including structural analysis, modal analysis of dynamic systems, and principal stress analysis. The significance of eigenvalues in fundamental engineering scenarios enhances the understanding of stability and response to loads.
Youtube Videos




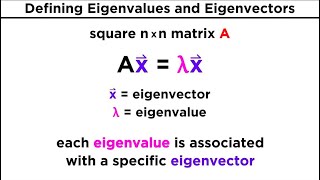

![Eigenvalues, Eigenvectors & Matrix Powers [IB Math AI HL]](https://img.youtube.com/vi/jGvJNHbwseg/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eigenvalues
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In civil engineering, many problems related to structural stability, vibration analysis, and systems of differential equations involve matrices. Among the most powerful tools for analyzing matrices are eigenvalues and eigenvectors. These concepts help us understand linear transformations, especially those that involve stretching, compressing, or rotating vectors. The knowledge of eigenvalues is essential for applications such as stability analysis of structures, principal stress analysis, and modal analysis in vibration problems. This chapter explores the theoretical foundations and computational techniques of eigenvalues, especially as they apply to real symmetric matrices, which often arise in civil engineering contexts.
Detailed Explanation
Eigenvalues are important in civil engineering fields because they provide insights into how structures respond under different conditions. They help engineers determine how materials will behave when forces are applied to them. For instance, when analyzing vibrations in a bridge, knowing the eigenvalues can tell us the natural frequencies at which the bridge will oscillate. Understanding these concepts allows engineers to design structures that will not only be safe but also effective at dissipating energy from forces such as wind or earthquakes.
Examples & Analogies
Imagine a guitar string. When you pluck the string, it vibrates at certain frequencies. The eigenvalues are similar to these frequencies: they tell us how the string (or in this case, a structure) will respond to being disturbed. If we know the eigenvalues (the natural frequencies), we can design the guitar (or bridge) to ensure it sounds good and can withstand strong vibrations without breaking.
Eigenvalues and Eigenvectors
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let A be an n×n square matrix. A scalar λ is called an eigenvalue of A if there exists a non-zero vector x∈Rn such that:
Ax=λx
Here:
• λ∈R (or C) is an eigenvalue,
• x is a corresponding eigenvector.
This equation can be rearranged as:
(A−λI)x=0
This is a homogeneous system of linear equations. For a non-trivial solution (x̸=0), the coefficient matrix must be singular, i.e.,
det(A−λI)=0
This is called the characteristic equation, and the polynomial det(A−λI) is the characteristic polynomial.
Detailed Explanation
In simpler terms, an eigenvalue is a special number associated with a matrix that shows how the matrix behaves when it transforms its vectors. The equation Ax = λx means that when you apply the matrix A to the vector x, the result is just a scaled version of x, where the scaling factor is the eigenvalue λ. To find these eigenvalues, we rearrange the equation to find the determinant of (A - λI) and set it to zero, which leads us to the characteristic polynomial that helps us identify the eigenvalues.
Examples & Analogies
Consider a rubber band. When you stretch it, you push it out from its rest position. The rubber band behaves in specific ways each time you let go; it will return to its original shape or vibrate. Similarly, when you apply transformations on vectors using a matrix, the eigenvalue helps you understand the scaling or change in direction of these vectors, akin to stretching and compressing that rubber band.
Characteristic Equation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is a homogeneous system of linear equations. For a non-trivial solution (x̸=0), the coefficient matrix must be singular, i.e.,
det(A−λI)=0
This is called the characteristic equation, and the polynomial det(A−λI) is the characteristic polynomial.
Detailed Explanation
The characteristic equation is crucial because it allows us to find eigenvalues. When we set up the equation det(A - λI) = 0, we are effectively finding cases where the transformation described by matrix A doesn't change the direction of some vector x, only its magnitude by a factor of λ. This leads us to the roots of the polynomial known as eigenvalues.
Examples & Analogies
Think of throwing a ball directly upward. It follows a parabolic path and eventually returns back to your hand. The characteristic equation helps to find the specific heights at which the ball reaches its apex before falling back down, similar to finding eigenvalues which indicate the special scaling factors in our transformations.
Computing Eigenvalues
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Steps to Find Eigenvalues
1. Start with the square matrix A.
2. Subtract λI from A to get A−λI.
3. Compute the determinant det(A−λI).
4. Solve the resulting characteristic polynomial p(λ)=0 for λ. These are the eigenvalues.
Detailed Explanation
Finding eigenvalues involves a straightforward set of steps. We begin with our matrix A, then create a new matrix by subtracting λ times the identity matrix I from A. By calculating the determinant of this new matrix and setting it to zero, we derive the characteristic polynomial, which offers a way to solve for our eigenvalues. Each root of this polynomial corresponds to an eigenvalue.
Examples & Analogies
Imagine baking a cake. You start with your ingredients (the matrix A), and then you add sugar and flour (the λI). Mixing them thoroughly (calculating the determinant) allows you to see how well the ingredients blend (the characteristic polynomial), ultimately letting you know how sweet or flavorful the cake (the eigenvalues) will be. Each unique flavor could represent a different eigenvalue.
Finding Eigenvectors
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For each eigenvalue λ:
1. Substitute λ into A−λI.
2. Solve (A−λI)x=0 to find the null space (eigenvectors).
Detailed Explanation
Once we have our eigenvalues, we can find the corresponding eigenvectors. For each eigenvalue we substitute back into our modified matrix (A−λI) and solve the resulting equation (A−λI)x=0. This allows us to determine the null space, which contains the eigenvectors that correspond to each eigenvalue. Essentially, these vectors signify the directions in which the transformation acts merely by scaling.
Examples & Analogies
Think of a road map. Each eigenvalue predicts how far you will go, while eigenvectors show you the specific routes you can take to reach your destination. If one road leads you to a park (an eigenvalue), the paths to that park from various starting points (the eigenvectors) give you the complete travel guide for those directions.
Key Concepts
-
Eigenvalues: Scalars that indicate how vectors are transformed by a matrix.
-
Eigenvectors: Vectors that remain in the same direction after a transformation, scaled by their eigenvalue.
-
Characteristic Polynomial: Used to derive eigenvalues from a square matrix.
-
Algebraic and Geometric Multiplicity: Key properties that describe the roots of a characteristic polynomial and corresponding vectors.
-
Diagonalization: A process of expressing a matrix as a product of its eigenvectors and eigenvalues.
Examples & Applications
In a stiffness matrix analysis for a structure, the eigenvalues reveal critical natural frequencies, indicating how the structure will respond to dynamic loads.
For a 2x2 matrix A = [[2, 1], [1, 2]], the eigenvalues can be calculated, helping to describe the behavior of the system the matrix represents.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Eigenvalue, eigenvector, stretching in a game, matrix's magic; you're never quite the same.
Stories
Imagine a glass stretching as you pour water in, that’s how eigenvalues show how much a vector can stretch in a transformation.
Memory Tools
Remember 'EVE' for eigenvalue, eigenvector, and eigenfunction to keep concepts straight in your mind!
Acronyms
Use 'MADE' for remembering
Matrix
Algebraic Multiplicity
Determinants
Eigenvalues.
Flash Cards
Glossary
- Eigenvalue
A scalar λ that indicates how a corresponding eigenvector changes when a linear transformation is applied to it.
- Eigenvector
A non-zero vector x that satisfies the equation Ax = λx, indicating a unique direction in a matrix transformation.
- Characteristic Polynomial
The polynomial obtained from det(A−λI)=0, used to find eigenvalues of a square matrix A.
- Algebraic Multiplicity
The number of times an eigenvalue appears as a root of the characteristic polynomial.
- Geometric Multiplicity
The number of linearly independent eigenvectors associated with a given eigenvalue.
- Diagonalizable
A property of a matrix that can be expressed as A = PDP⁻¹, where P contains eigenvectors and D contains eigenvalues.
- Real Symmetric Matrix
A matrix that is equal to its transpose and possesses real eigenvalues and orthogonal eigenvectors.
- Trace
The sum of the diagonal elements of a matrix, equal to the sum of its eigenvalues.
- Determinant
A scalar value that can be computed from the elements of a square matrix that provides information about the matrix, including eigenvalues.
Reference links
Supplementary resources to enhance your learning experience.
