Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Symmetric Matrices
Unlock Audio Lesson
Today we're going to discuss symmetric matrices. Can anyone tell me what a symmetric matrix is?
Isn't it a matrix that is equal to its transpose?
Correct! A matrix A is symmetric if A = A^T. This characteristic leads to some interesting properties regarding its eigenvalues and eigenvectors.
What are those properties?
Let's discuss eigenvalues first. All eigenvalues of a symmetric matrix are real. Can anyone guess why that might be useful?
Maybe because real numbers are easier to work with in engineering calculations?
Exactly! Working with real eigenvalues simplifies many applications. Now, let’s talk about orthogonality of eigenvectors.
What does orthogonality mean in this context?
Orthogonality means that the eigenvectors corresponding to distinct eigenvalues are perpendicular to each other. This is a powerful property since it helps in diagonalization.
How is diagonalization related to engineering?
Great question! Diagonalization helps simplify matrices, making it easier to solve systems of equations that arise in structural analysis. To summarize, symmetric matrices have real eigenvalues and orthogonal eigenvectors, making them particularly advantageous in applications like finite element methods.
Diagonalization of Symmetric Matrices
Unlock Audio Lesson
Now, let's dive deeper into the diagonalization of symmetric matrices. How is it carried out?
Do we need the eigenvectors for diagonalization?
Yes! A symmetric matrix can be diagonalized as A = QDQT, where Q is the orthogonal matrix of eigenvectors, and D is the diagonal matrix of eigenvalues. Why do you think using an orthogonal matrix is beneficial?
Because orthogonal matrices preserve lengths and angles, right?
Exactly! This characteristic is significant in engineering to ensure that the analysis of structures remains accurate. Can anyone share how we would apply this in civil engineering?
In stress analysis, for example, we can represent the stress tensor using symmetric matrices to simplify calculations.
Perfect! Always remember, symmetric matrices are crucial in structural analysis due to the simplicity they provide in calculations and in ensuring stability in modeling.
Applications of Symmetric Matrices in Engineering
Unlock Audio Lesson
Let’s talk about where symmetric matrices are applied in civil engineering. Who can give me an example?
I think they are used in structural analysis for determining stress.
Absolutely! The stress tensor in mechanics is a symmetric matrix, which means we can leverage all the properties we've discussed. Why do you think this is advantageous?
Because it allows us to simplify complex calculations about stress distribution in materials.
Correct! Even more, having real eigenvalues means we can directly interpret them as principal stresses. What about the interpretation of eigenvectors?
They represent the principal directions of the stresses, right?
That's right! So, to recap, symmetric matrices are integral in modeling stresses in civil engineering and ensure that we can perform accurate and stable analyses of structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
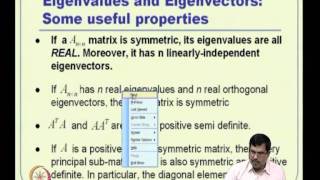
In the context of symmetric matrices, all eigenvalues are real, and the eigenvectors corresponding to distinct eigenvalues are orthogonal. Symmetric matrices can be diagonalized using an orthogonal matrix, which is vital in certain applications like stress analysis and finite element methods.
Detailed
In this section, we delve into the special case of symmetric matrices, defined as matrices where A = A^T. Key properties include that all eigenvalues are real, and eigenvectors associated with distinct eigenvalues are orthogonal to each other. This orthogonality and the reality of eigenvalues make symmetric matrices uniquely advantageous, especially when it comes to diagonalization. A symmetric matrix A can be represented as A = QDQT, where Q is an orthogonal matrix and D is a diagonal matrix. This property is particularly significant in civil engineering applications, including stress analysis and finite element methods, where the stability and behavior of structures are of utmost importance. Understanding these properties allows engineers to effectively analyze and predict the response of structures subjected to various forces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Real Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A∈Rn×n be symmetric (A=AT). Then:
• All eigenvalues are real.
Detailed Explanation
When we have a symmetric matrix, which means the matrix is equal to its transpose (A = AT), a significant property arises: all of its eigenvalues are real numbers. This stands in contrast to non-symmetric matrices, which can have complex eigenvalues. This property of symmetric matrices is crucial because real eigenvalues indicate that the transformations represented by these matrices maintain certain geometric interpretations.
Examples & Analogies
Imagine a perfectly balanced seesaw. Just like how one person’s weight on one side needs to be balanced by another's weight on the other side for it to stay horizontal, symmetric matrices ensure that their eigenvalues, which embody various properties, are balanced in the real number system. This means that the transformations involving these matrices maintain stability, much like balance on a seesaw.
Orthogonal Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Eigenvectors corresponding to distinct eigenvalues are orthogonal.
Detailed Explanation
This property states that if two eigenvalues of a symmetric matrix are different, then the corresponding eigenvectors associated with those eigenvalues are orthogonal to each other. Orthogonality here means that the dot product of those eigenvectors is zero, which geometrically implies that they are at right angles to each other in the vector space. This characteristic is vital in various applications, as it simplifies computations and allows for the construction of orthogonal bases.
Examples & Analogies
Consider the concept of two distinct hiking trails leading in different directions; if one trail goes due north and the other goes due east, they are 'orthogonal' paths. Similarly, in a symmetric matrix, distinct eigenvectors represent directions where their combined transformations do not interfere, just as the two trails remain independent of one another, providing clear paths without overlap.
Diagonalization by an Orthogonal Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• A can be diagonalized by an orthogonal matrix: A=QDQT.
Detailed Explanation
The property of symmetric matrices allows them to be diagonalized using an orthogonal matrix, expressed as A = QDQT, where Q is the orthogonal matrix containing the eigenvectors and D is a diagonal matrix with the corresponding eigenvalues. Diagonalization is an efficient way to simplify matrix operations, as it transforms complex matrix computations into simple multiplication involving diagonal matrices, which are much easier to handle.
Examples & Analogies
Imagine sorting books on a shelf. If you have a messy shelf (the original matrix A), and you take out the books and line them up in a neat order (the diagonal matrix D), you simplify identifying and accessing each book. The orthogonal matrix Q represents how you positioned them back in line on the shelf, allowing for easy reach and retrieval. Just like the sorted shelf reduces chaos, diagonalization streamlines calculations involving symmetric matrices.
Applications in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is especially relevant in stress analysis and finite element methods (FEM).
Detailed Explanation
The properties of symmetric matrices play a crucial role in engineering fields, particularly in stress analysis and finite element methods (FEM). In stress analysis, the stress tensors are symmetric, facilitating the calculation of principal stresses and directions in structural engineering. Finite element methods use these properties to analyze complex structures, making computations more efficient and reliable due to the diagonalization of stiffness matrices.
Examples & Analogies
Think of an architect designing a bridge. The architect must understand how different forces (like weight and wind) will affect the structure. Symmetric matrices help the architect calculate stresses and strains inside the bridge components, ensuring the design can withstand these forces—much like an artist measures exact angles to ensure their sculpture stands upright without toppling over.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Symmetric Matrices: Matrices that are equal to their transpose, possessing properties such as real eigenvalues.
-
Diagonalization: Process of converting a matrix into a diagonal form, useful for simplifying matrix operations.
-
Orthogonality of Eigenvectors: Distinct eigenvectors of symmetric matrices are perpendicular, enhancing analysis and calculations in engineering.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A matrix A = [[2, 1], [1, 2]] is symmetric and can be analyzed for its eigenvalues and eigenvectors.
-
In stress analysis, the stress tensor, which is symmetric, allows engineers to find principal stresses and directions using properties of eigenvalues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Symmetric matrices, oh so fair, Real eigenvalues, they're always there.
📖 Fascinating Stories
-
Imagine a wise engineer named Symon who could always find his true eigenvalues, never complex, and with his orthogonal friends, the eigenvectors, he ensured every structure stood strong and true.
🧠 Other Memory Gems
-
Remember 'S.O.R.E': Symmetric means real eigenvalues, Orthogonal eigenvectors, and Easy diagonalization.
🎯 Super Acronyms
S.O.L
- Symmetric for real
- Orthogonal for unique vectors
- and Linear diagonalization.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Symmetric Matrix
Definition:
A matrix that is equal to its transpose.
-
Term: Eigenvalue
Definition:
A scalar λ such that there exists a non-zero vector x where Ax = λx.
-
Term: Eigenvector
Definition:
A vector associated with an eigenvalue representing a direction of transformation.
-
Term: Orthogonal Matrix
Definition:
A square matrix whose columns and rows are orthogonal unit vectors.