Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Power Method
Unlock Audio Lesson
Today we're going to cover the Power Method, an essential numerical technique for finding the dominant eigenvalue of a matrix. Does anyone know what we mean by 'dominant eigenvalue'?
Is that the eigenvalue with the largest magnitude?
Exactly! The dominant eigenvalue is indeed the one with the highest magnitude. This method is particularly useful for large matrices that we see in structural engineering contexts. What do we mean by large matrices?
Matrices that have many rows and columns, right?
Correct! So, in civil engineering, we often deal with large and complex matrices when modeling structures. Let's break down the steps of the Power Method.
Steps of the Power Method
Unlock Audio Lesson
The Power Method consists of a series of steps. First, we start with a square matrix A and an initial guess vector x₀. Can anyone tell me what we do first?
We normalize the initial vector x₀?
Correct! Normalizing ensures that the vector has a magnitude of 1. Then, we proceed to calculate y = Ax<sub>k-1</sub>. Why do you think we need to compute y?
To figure out how the matrix A transforms our vector?
Precisely! And then we find the norm of y to estimate the next vector. This process continues iteratively until we converge on our dominant eigenvalue. It's like zooming in on the most significant direction in our transformations.
Convergence Conditions
Unlock Audio Lesson
Now that we understand the steps, let's talk about convergence. What conditions must be met for the Power Method to work effectively?
The matrix has to have a unique dominant eigenvalue?
That's right! The uniqueness ensures that our iterations will actually converge. And what about our initial vector x₀?
It should be in the direction of the dominant eigenvector?
Exactly! If it doesn't have a component in that direction, we might not converge to the right eigenvalue. Understanding this is key to successful application in civil engineering scenarios.
Applications in Civil Engineering
Unlock Audio Lesson
Let's connect the Power Method with civil engineering applications. Where do you think this method could be particularly useful?
Maybe in analyzing the vibrations of buildings?
Exactly! It can help estimate the fundamental natural frequencies of tall buildings. Can anyone think of how that would assist in structural design?
It ensures the building can withstand different forces without collapsing!
Right again! The Power Method aids engineers in making informed decisions about structural integrity.
Conclusion and Summary
Unlock Audio Lesson
To summarize, we learned that the Power Method is a practical tool for finding the dominant eigenvalue and its corresponding eigenvector of large matrices, particularly useful in civil engineering. What are the key points we've discussed?
It has steps that involve normalizing the initial vector and iterating until convergence.
And we need certain conditions to ensure it works!
It's used in structural analysis for things like vibrations!
Perfect! You've all grasped the critical concepts of the Power Method.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section details the Power Method, which is an iterative numerical approach designed to compute the dominant eigenvalue and its eigenvector. The method is categorized under numerical methods for eigenvalue computation, making it particularly applicable in civil engineering for analyzing structural dynamics and stability.
Detailed
Power Method for Dominant Eigenvalue
The Power Method is an iterative numerical algorithm used for finding the dominant eigenvalue (the eigenvalue of largest magnitude) of a matrix, as well as its corresponding eigenvector. It is particularly effective for large and sparse matrices, characteristics often found in finite element models of civil engineering structures.
Key Points:
- Algorithm Steps:
- Start with a square matrix A and an initial guess vector x₀.
- Normalize x₀.
- For each iteration k, calculate:
- y = Axk-1
- µ = ||y|| (the norm of y)
- Update xk = yk / ||yk||.
- As k approaches infinity, this process converges to the dominant eigenvector, with µ converging to the dominant eigenvalue.
- Convergence Conditions:
- The matrix must have a unique dominant eigenvalue, and the initial vector should have a component in the direction of the dominant eigenvector.
- Application in Civil Engineering:
- The Power Method is significant for estimating the fundamental natural frequency and mode shapes of tall buildings and long bridges, crucial for ensuring structural stability.
Youtube Videos
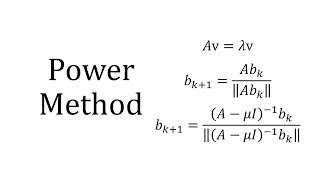
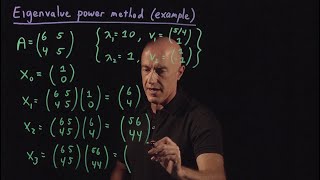
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Power Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Power Method is a numerical iterative algorithm for finding the dominant eigenvalue (i.e., the eigenvalue of largest magnitude) and its corresponding eigenvector of a matrix. This is especially useful when the matrix is large and sparse, which is often the case in finite element models of civil structures.
Detailed Explanation
The Power Method is designed to find the largest eigenvalue of a matrix, which is important in various applications, such as structural engineering. If you have a large matrix, it can be challenging to compute its eigenvalues directly, and the Power Method offers a systematic way to approximate the dominant eigenvalue and its associated eigenvector using iterative calculations.
Examples & Analogies
Consider a tall building swaying in the wind. The dominant eigenvalue corresponds to the building's fundamental natural frequency, which determines how it will respond to environmental forces. Just like measuring how high a swing goes can help us understand how it moves, the Power Method helps engineers predict structural responses reliably.
Algorithm Steps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Algorithm Steps:
Given a matrix A∈Rn×n, and an initial guess vector x0, perform the following:
1. Normalize x0, i.e., x0 := ∥x0∥
2. For k = 1, 2,...:
• y = Axk−1
• µ = ∥yk∥
• x = yk/∥yk∥
As k → ∞, xk → x (an eigenvector), and µ → λ (the dominant eigenvalue).
Detailed Explanation
The algorithm consists of the following steps: First, you start with a matrix A and an initial guess for an eigenvector. The first step is to normalize this guess, ensuring its length is equal to one. Then, in a loop, you repeatedly multiply the matrix A by your current vector, yielding a new vector y. The dominant eigenvalue is approximated using the norm (length) of this new vector. Finally, the algorithm updates your guess for the eigenvector, continuing until the result stabilizes.
Examples & Analogies
Imagine you’re trying to find the fastest runner in a race. You start with a guess of who might be the fastest (your initial vector). As the race progresses (iterations), you keep updating your estimate based on who crosses the finish line first (multiplying by the matrix). Eventually, you’ll have a clear winner (the dominant eigenvector), who you can identify with confidence.
Convergence Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Convergence Conditions:
• The matrix must have a unique eigenvalue λ such that |λ| > |λ1| ≥ ... ≥ |λn|.
• The initial vector x0 must have a component in the direction of the dominant eigenvector.
Detailed Explanation
For the Power Method to work effectively, two conditions must be met. First, there needs to be a dominant unique eigenvalue that is larger in magnitude than all other eigenvalues of the matrix. Second, the initial guess for the eigenvector must not be completely orthogonal (i.e., at a 90-degree angle) to the direction of that dominant eigenvector, as that would prevent the algorithm from accurately converging toward the desired solution.
Examples & Analogies
Think of tuning a musical instrument like a guitar. If your starting note (initial vector) is too far from the actual note (dominant eigenvalue), it will take longer to tune it right. Likewise, if you’re specifically trying to find a high note in a song (dominant eigenvalue), starting close to that note helps you identify it faster.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Use in Civil Engineering:
Used for estimating the fundamental natural frequency (first mode shape) of tall buildings and long bridges modeled by stiffness and mass matrices.
Detailed Explanation
In civil engineering, the Power Method is commonly used to estimate the fundamental natural frequency of structures. This frequency is crucial because it indicates how a structure will respond to dynamic loads, such as wind or seismic activities. Accurately estimating this frequency helps engineers design safer structures by ensuring they can withstand environmental forces without undergoing excessive movement or failure.
Examples & Analogies
Imagine a tightrope walker on a high wire. Just as the walker sways back and forth at a particular frequency based on their movements and the wire's tension, engineers need to know that frequency for buildings and bridges to ensure they remain stable during events like earthquakes. The Power Method helps them find that frequency quickly and efficiently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Iterative Algorithm: The Power Method is an iterative approach to approximate eigenvalues.
-
Dominant Eigenvalue: The eigenvalue with the highest magnitude critical for applications in engineering.
-
Normalization: The process of transforming the initial vector to unit length for effective iterations.
-
Convergence Conditions: Specific requirements that need to be fulfilled for the method to produce reliable results.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider a large stiffness matrix from a three-dimensional model of a building; using the Power Method, the dominant eigenvalue can indicate the fundamental frequency of vibrations.
-
In structural analysis, applying the Power Method can reveal the dominant mode shapes when analyzing the response of tall structures under various loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the eigenvalue that's supreme, use Power Method, it's a dream.
📖 Fascinating Stories
-
Imagine a tall building where engineers use the Power Method, climbing higher and higher to find the strongest support, just like climbing to the roof to see the whole city!
🧠 Other Memory Gems
-
N → Normalize; A → Apply matrix; N → Normalize again; D → Determine next vector (NAND).
🎯 Super Acronyms
P.A.N.D
- Power
- A
- Next
- Determine - to remember the steps.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Power Method
Definition:
An iterative algorithm for finding the dominant eigenvalue of a matrix.
-
Term: Dominant Eigenvalue
Definition:
The eigenvalue of a matrix with the largest magnitude.
-
Term: Eigenvector
Definition:
A vector that, when multiplied by the matrix, results in a scaled version of itself.
-
Term: Convergence
Definition:
The process of approaching a limit or the dominant eigenvalue through iterations.
-
Term: Normalization
Definition:
The process of adjusting a vector to have a magnitude of one.