Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvalues
Unlock Audio Lesson
Today, we will explore eigenvalues. An eigenvalue is a special scalar related to a square matrix. Can anyone define it in their own words?
Isn’t it like a number that describes how a matrix transforms a vector?
Exactly! When a matrix transforms a vector, it can stretch or compress it. This scalar λ is significant in many applications. What do you think is needed to find λ?
I believe we need to create the characteristic polynomial, right?
Yes! We compute the determinant of (A−λI). This is crucial. Can someone remind me what the characteristic polynomial represents?
It shows where the matrix is singular?
Exactly! Where the determinant equals zero leads us to eigenvalues. Well done, everyone.
Finding Eigenvalues
Unlock Audio Lesson
Let's discuss how to compute eigenvalues step by step. Starting with matrix A, what’s the first action?
We subtract λI from A.
Correct! After that, we move on to compute the determinant. What comes next once we have the determinant?
We need to solve p(λ) = 0?
Correct again! This gives us the eigenvalues. Now, who can tell me how we identify the corresponding eigenvectors?
By plugging the eigenvalue back into the equation (A-λI)x=0!
Well done! You’ve summarized the process. Let's summarize: First we get eigenvalues, then solve for eigenvectors.
Finding Eigenvectors
Unlock Audio Lesson
Now that we understand eigenvalues, let’s focus on finding their corresponding eigenvectors. What steps do we take?
We substitute the eigenvalue into the matrix equation.
Exactly! And what does it mean to solve the equation (A-λI)x=0?
We find the null space and the eigenvectors!
Correct! Finding eigenvectors is about determining the vectors that correspond to each eigenvalue by solving for the null space. Great teamwork!
Applications of Eigenvalues and Eigenvectors
Unlock Audio Lesson
Finally, let’s discuss why eigenvalues and eigenvectors matter, especially in civil engineering. How do they apply?
They help us analyze stability and vibrations in structures?
Absolutely! Eigenvalues relate to natural frequencies and stability criteria in structures. Can anyone give me a specific example?
In buckling analysis, right? We deal with eigenvalue problems to determine failure modes.
Exactly! Understanding eigenvalues helps engineers design safer buildings. Final thoughts on why they are so important?
They simplify complex systems and help predict structural behavior.
Well said! They are critical tools in both analysis and design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the steps to find eigenvalues and corresponding eigenvectors of square matrices. It explains how to derive the characteristic polynomial and solve for both eigenvalues and eigenvectors, highlighting their importance in structural analysis and other applications.
Detailed
Detailed Summary
This section elaborates on the methodology for computing eigenvalues and eigenvectors, critical concepts in linear algebra with profound implications in civil engineering. Steps for finding eigenvalues involve starting from a square matrix A, subtracting λI, computing the determinant, and solving the characteristic polynomial p(λ)=0, which reveals the eigenvalues.
To find corresponding eigenvectors for each derived eigenvalue, one substitutes λ back into the modified matrix (A−λI) and solves the equation (A−λI)x=0. This process leads to the identification of the null space of the matrix corresponding to each eigenvalue. The section emphasizes the significance of these concepts in analyzing structural stability, vibration behavior, and other engineering systems.
Youtube Videos
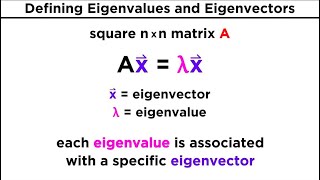
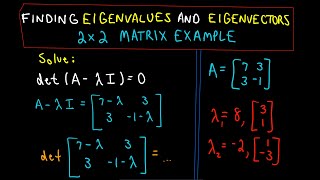
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Steps to Find Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Start with the square matrix A.
- Subtract λI from A to get A−λI.
- Compute the determinant det(A−λI).
- Solve the resulting characteristic polynomial p(λ)=0 for λ. These are the eigenvalues.
Detailed Explanation
To find eigenvalues of a given square matrix A, you need to follow several systematic steps. First, identify the matrix A you are working with. Next, you subtract the product of the eigenvalue (denoted as λ) and the identity matrix I from A. This operation gives you a new matrix labeled A−λI. The next step involves computing the determinant of this new matrix. The determinant is a scalar value that can tell us about the invertibility and properties of the matrix. Finally, to find the eigenvalues, solve the equation formed by setting the determinant to zero. The solutions to this equation give you the eigenvalues of the matrix.
Examples & Analogies
Think of this process as trying to find the roots of a polynomial, similar to how you’d find the points where a curve crosses the x-axis. In this analogy, the square matrix A represents the shape of the curve, and λ values that satisfy the characteristic polynomial (the points where the determinant is zero) represent the points where that curve crosses. Just like different roads can lead you to a destination, different methods (determinants, matrices) help you find eigenvalues.
Steps to Find Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For each eigenvalue λ:
1. Substitute λ into A−λI.
2. Solve (A−λI)x=0 to find the null space (eigenvectors).
Detailed Explanation
Once you have the eigenvalues, the next task is to compute the corresponding eigenvectors. For each eigenvalue λ that you found earlier, you substitute it back into the matrix equation A−λI that you derived. This gives you a new matrix. The next step is to solve the system of linear equations represented by (A−λI)x=0. The solutions to this equation are known as the eigenvectors. Essentially, they describe the directions in which the transformation associated with the matrix A acts by stretching or compressing vectors.
Examples & Analogies
You can think of eigenvectors as specific directions in which something moves or operates, like a wind blowing in different directions. Just as a wind gauge detects where the wind is blowing strongest (its direction), the process of solving (A−λI)x=0 helps us discover the vectors (directions) that 'survive' the transformation defined by A without changing their direction, hence revealing the underlying structure of the matrix.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: A scalar indicating the factor by which a corresponding eigenvector is scaled during transformation.
-
Eigenvector: A vector that remains in the same direction after a transformation by a matrix A.
-
Characteristic Polynomial: A polynomial derived from the determinant that helps identify eigenvalues.
-
Null Space: The collection of vectors that satisfy the equation (A-λI)x=0.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For matrix A = [[2, 1], [1, 2]], the eigenvalues are found by solving det(A-λI)=0, leading to λ=1, 3.
-
If λ=3 is an eigenvalue for matrix A, the corresponding eigenvector x can be found by solving (A-3I)x=0.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues help us see, how matrix turns a vector free.
📖 Fascinating Stories
-
Imagine a stretching spring; the eigenvalue tells how far it’ll spring.
🧠 Other Memory Gems
-
A-E-I-O-U: A for Apply, E for Eigenvalue, I for Identify, O for Obtain, U for Understand.
🎯 Super Acronyms
EVE
- Eigenvalues
- Vectors
- Eigenvalue equation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ that satisfies the equation Ax = λx for a square matrix A and a non-zero vector x.
-
Term: Eigenvector
Definition:
A non-zero vector x that, when multiplied by a square matrix A, results in a scalar multiple of itself (Ax = λx).
-
Term: Characteristic Polynomial
Definition:
A polynomial obtained by calculating the determinant of (A−λI), which is used to find eigenvalues.
-
Term: Null Space
Definition:
The set of all vectors x that satisfy the equation (A-λI)x=0, containing the eigenvectors corresponding to eigenvalue λ.