Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues in Stability
Unlock Audio Lesson
Today, we begin by exploring how eigenvalues help us understand the stability of structures. Can anyone explain what an eigenvalue is in a nutshell?
I think an eigenvalue is a scalar that helps in solving matrix equations?
That's correct! Eigenvalues are indeed scalars that relate to linear transformations of vectors. Specifically, in structural analysis, they help analyze stability. Can anyone tell me what happens when a structure reaches a critical load?
It can buckle or become unstable.
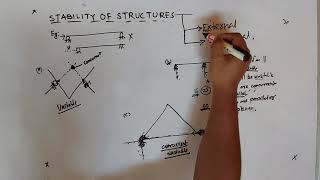
Exactly! When we analyze structures for stability, we focus on the eigenvalues derived from the equation (K - λG)x = 0. Here, K is the stiffness matrix and G represents the geometric stiffness matrix.
So, larger eigenvalues would mean the structure is stiffer?
Yes! Larger eigenvalues indicate stiffer modes that resist buckling. Let’s summarize: Eigenvalues help us predict critical loads, ensuring the structural integrity of designs.
Buckling Analysis
Unlock Audio Lesson
Now, let's focus on buckling, which is a primary concern in structural design. When do we say a structure is experiencing buckling?
Isn’t buckling when a structure deforms under load and loses stability?
Correct! We can analyze buckling using eigenvalue methods. Can someone explain how we derive the characteristic equation for buckling analysis?
I think it comes from setting the determinant of the matrix to zero, right?
Exactly! The characteristic equation helps us find the eigenvalues. These eigenvalues correspond to the critical loads at which buckling occurs. Remember, smaller eigenvalues tend to signify more flexibility and a higher risk of buckling.
So, if we have multiple eigenvalues, we can analyze different modes of buckling?
Absolutely! Each eigenvalue can represent a different mode of failure or instability. Let's summarize key points: eigenvalues relate directly to stability and buckling analysis.
Practical Applications
Unlock Audio Lesson
In our final session, let's discuss how these concepts apply in real-world scenarios. Can you think of scenarios in civil engineering where stability is a key concern?
Maybe in tall buildings during high winds or earthquakes?
Exactly! The stability of high-rise buildings is critical, especially under dynamic loads. Eigenvalue analysis helps determine the natural frequencies and mode shapes, which are crucial for maintaining stability during such events.
Does this mean that every structure has specific eigenvalues that engineer need to calculate?
Yes, each structure will have unique eigenvalues that must be calculated to ensure safety and effectiveness. Understanding these values helps engineers design safer structures, ensuring they can withstand various loads without buckling.
This is all making sense now! It’s amazing how math relates to building safety.
Great! Recap: Eigenvalues are vital in predicting structural stability and buckling. They empower engineers to create safe, resilient designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvalues are crucial for stability analysis in civil engineering, particularly in determining structural behavior under load. The relation of eigenvalues to the buckling of structures highlights their application in predicting critical loads and modes of instability.
Detailed
Stability of Structures
In civil engineering, the stability of structures is a fundamental concern, especially under various loading conditions. Eigenvalues play a critical role in assessing the stability of structural systems through buckling analysis. The equation derived from the stiffness and geometric stiffness properties of a structure,
(K - λG)x = 0,
provides insight into the critical load at which a structure may become unstable. Large eigenvalues indicate stiff modes that resist deformation, while small eigenvalues correspond to flexible modes that are more susceptible to buckling. By solving eigenvalue problems, engineers can identify critical modes and assess the load-carrying capacity of various structural configurations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Buckling Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Buckling analysis involves eigenvalue problems:
(K−λG)x=0
Where K is the stiffness matrix and G is the geometric stiffness matrix.
Detailed Explanation
Buckling analysis is a critical aspect of understanding when and how structures can fail under certain loads. This analysis can be modeled using an eigenvalue problem presented in the form (K - λG)x = 0. Here, K is known as the stiffness matrix, which represents how a structure deforms under load, while G is the geometric stiffness matrix, which accounts for the effects of the structure's geometry on its stability. The variable λ represents the eigenvalue that indicates the critical load point at which buckling occurs.
Examples & Analogies
Think of a long, slender column that you might see in a building. If the column is pushed too hard, it can buckle. Imagine a pencil that you try to bend between your fingers. If you push too hard and it bends suddenly, that’s akin to reaching the critical load. The analysis helps engineers determine how much load that column can handle before it buckles.
Dynamic Behavior Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The dynamic behavior of buildings, bridges, and other structures is analyzed using eigenvalue problems. The eigenvectors represent mode shapes and the eigenvalues represent natural frequencies.
Detailed Explanation
In structural engineering, understanding how structures respond to dynamic loads—such as wind, earthquakes, or impacts—is crucial. Eigenvalue problems help analyze this response by determining the natural frequencies at which structures vibrate. The associated eigenvectors describe the 'mode shapes,' indicating how different parts of the structure move relative to each other. Identifying these frequencies is crucial for designing structures that can withstand dynamic forces without resonating or failing.
Examples & Analogies
Imagine a swing on a playground; it has a natural rhythm when you push it. If you push it at just the right moment, you can make it go higher—this is like finding the natural frequency of the swing. Now, picture a large bridge swaying in the wind, needing to avoid resonating to ensure safety. Engineers have to calculate its modes of vibration to ensure it is designed safely.
Stress Analysis Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In stress analysis, the stress tensor is symmetric. The eigenvalues of the stress matrix are the principal stresses, and the eigenvectors indicate the principal directions.
Detailed Explanation
In the context of stress analysis, particularly in materials and structures, the stress tensor represents internal forces. Since this tensor is symmetric, it has real eigenvalues, which are interpreted as principal stresses—the maximum and minimum normal stresses occurring at a point in a material. The corresponding eigenvectors indicate the principal directions in which these stresses act—essentially telling engineers the most critical angles at which to analyze material failure.
Examples & Analogies
Consider a rubber band. When you pull on it, different parts of the band experience different amounts of stress. The points where the rubber band is most likely to break can be thought of as principal stresses. Knowing where these stresses are can help you reinforce the rubber band at those points to prevent it from breaking.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues predict the critical loads at which buckling occurs in structures.
-
Stability is determined through eigenvalue analysis in structural contexts.
-
The relationship between eigenvalues and stiffness matrices is fundamental for stability assessments.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A tall building undergoing wind loading may experience specific eigenvalues that can be calculated to analyze its stability under lateral forces.
-
In bridge designs, eigenvalue analysis helps ensure that critical loads do not lead to buckling or structural failure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When structures strain and start to sway, eigenvalues help show the way.
📖 Fascinating Stories
-
Imagine a tall tower standing still; it wobbles when loads apply force or thrill. Eigenvalues whisper secrets in the mix—their values, the load, the balance fix.
🧠 Other Memory Gems
-
When analyzing structures, remember 'EBS': Evaluate Buckling Stability using eigenvalue insights.
🎯 Super Acronyms
Buckling's analysis focuses on '**B.E.S.T.**'
- Buckling Eigenvalues Stability Testing.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar associated with a linear transformation represented by a matrix, reflecting the factor by which an eigenvector is scaled.
-
Term: Stability
Definition:
The capability of a structure to maintain its position and not deform under loading.
-
Term: Buckling
Definition:
A sudden failure mode of a structural member subjected to high compressive stress, leading to a large deformation.
-
Term: Stiffness Matrix (K)
Definition:
A matrix representing the stiffness properties of a structure used in structural analysis.
-
Term: Geometric Stiffness Matrix (G)
Definition:
A matrix that represents the geometric contributions to the stiffness of a structure due to loads and deflections.