Cayley-Hamilton Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cayley-Hamilton Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will talk about the Cayley-Hamilton Theorem. Can anyone tell me what it is?

Is it related to matrices?

Exactly! The Cayley-Hamilton Theorem states that every square matrix satisfies its own characteristic equation. What do you think this implies?

Maybe it helps in solving matrix equations?

Correct! This theorem allows us to express higher powers of a matrix in terms of lower powers. We can write its characteristic polynomial as p(λ) = det(A - λI), and then substituting A into this gives us a polynomial that equals zero.
Significance of the Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss why this theorem is important. Can someone think of applications?

It could help in manipulating matrices for solving equations!

Absolutely! In civil engineering, it simplifies complex calculations involving dynamic simulations. Can you name any specific applications?

What about computing powers of a matrix?

Yes! This theorem is crucial for efficient computation of matrix powers. It also helps in reducing high-order differential systems by expressing higher-order terms via lower-order ones.
Practical Calculations with the Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at practical calculations using the Cayley-Hamilton Theorem. How would you start if asked to find M^2 if M satisfies its characteristic equation?

I would identify the characteristic polynomial and substitute the matrix into it, right?

Precisely! By using p(M) = 0, we simplify M^2 or higher powers effectively. What advantage does this give us in terms of computational work?

It reduces computational time because we rely on the lower powers instead of calculating it directly.

Exactly! This theorem is a powerful tool in our toolkit.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The theorem is significant in various applications such as matrix functions, computation of matrix powers, and reduction of high-order differential systems. It simplifies calculations in engineering problems involving matrices.
Detailed
Cayley-Hamilton Theorem
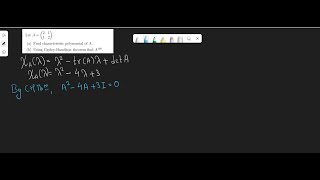
The Cayley-Hamilton Theorem posits that any square matrix, denoted as A ∈ R^n×n, satisfies its own characteristic equation. This characteristic equation can be derived from the matrix's determinant, formulated as:
$$p(λ) = det(A−λI) = λ^n + a_n λ^{n−1} + ... + a_1 λ + a_0$$
Substituting the matrix A into this polynomial gives:
$$p(A) = A^n + a_n A^{n−1} + ... + a_1 A + a_0 I = 0$$
Applications:
- Matrix Functions and Inversion: Simplifies the process for higher-order matrix operations.
- Efficient Computation of Matrix Powers: Essential for reducing computational effort.
- Reduction of High-Order Differential Systems: Helps manage complex systems encountered in engineering analysis.
The theorem finds particular significance in fields like civil engineering, streamlining repeated matrix multiplications in dynamic simulations of structures.
Youtube Videos

![Cayley-Hamilton Theorem [Control Bootcamp]](https://img.youtube.com/vi/PrfxmkBsYKE/mqdefault.jpg)







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Statement of the Cayley-Hamilton Theorem
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Cayley-Hamilton Theorem states that every square matrix satisfies its own characteristic equation.
Detailed Explanation
The Cayley-Hamilton Theorem is a fundamental result in linear algebra that applies to square matrices. It states that if we have a square matrix A and its characteristic polynomial, p(λ), then if we replace λ with the matrix A in that equation, the result is the zero matrix. This means that A behaves in some ways as if it were a number when substituted into its own polynomial equation.
Examples & Analogies
Imagine a famous recipe that is so detailed, it even lists the exact dosages of all ingredients. When you make the dish according to the recipe and taste it, it perfectly embodies the essence of the recipe. Similarly, in the Cayley-Hamilton theorem, the matrix A reflects its 'recipe' in its own characteristic polynomial.
Characteristic Polynomial
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let A∈Rn×n and its characteristic polynomial be:
p(λ)=det(A−λI)=λn+a λn−1+···+a λ+a
1 n−1 n
Detailed Explanation
The characteristic polynomial of a matrix A is formed by taking the determinant of the matrix (A - λI), where I is the identity matrix and λ is a scalar. The polynomial has a degree equal to the size of the matrix (n). It is structured in such a way that when you solve the characteristic polynomial set to zero, you find the eigenvalues of the matrix A.
Examples & Analogies
Think of the characteristic polynomial as a treasure map where x marks the spot. The journey defined by the polynomial leads us to the eigenvalues, which are like hidden treasures within the matrix. Each eigenvalue corresponds to a special ‘treasure’ that holds important properties of the matrix.
Applying the Cayley-Hamilton Theorem
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Then:
p(A)=An+a An−1+···+a A+a I =0
1 n−1 n
Detailed Explanation
When we apply the Cayley-Hamilton theorem to a matrix A, we plug A back into its own characteristic polynomial instead of λ. The result states that the combination of powers of A (like A raised to various powers) has a special relationship that ultimately sums to the zero matrix. This is particularly useful for computing functions of matrices and simplifying calculations involving powers of matrices.
Examples & Analogies
Consider an artist who, after creating a masterpiece, decides to paint a sequel that reflects the themes and styles of the original painting. Just as the sequel can be derived from the original, substituting the matrix A into its own polynomial allows us to work with it in more complex scenarios, such as matrix powers or exponential functions, while keeping in mind its inherent properties.
Applications of the Cayley-Hamilton Theorem
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applications:
- Matrix functions and inversion.
- Efficient computation of matrix powers.
- Reduction of high-order differential systems.
Detailed Explanation
The Cayley-Hamilton theorem has several practical applications in engineering and applied mathematics. It allows for the evaluation of matrix functions such as exponential and logarithmic functions of matrices. It helps compute matrix powers efficiently without directly multiplying the matrix many times over. Furthermore, it can also be used to reduce higher-order differential equations to first-order systems, making them simpler to solve.
Examples & Analogies
Imagine trying to compute the growth of a complex tree (a high-order problem). Instead of fighting to manage every branch (power) directly, you can use the Cayley-Hamilton theorem to understand the fundamental patterns in the tree's growth, making it easier to analyze and predict its expansion more efficiently, akin to managing simpler linear growths.
Cayley-Hamilton Theorem in Civil Engineering
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Civil Engineering Use: Simplifies calculations involving repeated matrix multiplications in dynamic simulations of structures.
Detailed Explanation
In civil engineering, dynamic simulations often require modeling structures under various loads and conditions. The Cayley-Hamilton theorem simplifies the computational processes by allowing engineers to use matrix exponentiation and manipulate these matrices efficiently, significantly speeding up simulations, especially when dealing with repeated calculations in larger models.
Examples & Analogies
Think of an architect designing a large complex structure like a bridge. Instead of recalculating each stress point every time a load changes, the Cayley-Hamilton theorem lets them streamline their calculations, similar to having an advanced calculator that swiftly churns out numbers, freeing the architect to focus on the design's creativity and safety.
Key Concepts
-
Characteristic equation: The equation that a square matrix satisfies, derived from its determinant.
-
Applications: The theorem’s use in simplifying calculations for matrix powers and differential equations.
Examples & Applications
If a matrix A satisfies p(A) = 0, then this implies that A can be manipulated using its characteristic polynomial.
Using the Cayley-Hamilton theorem, if A is a 2x2 matrix with determinant given, one could find A^2 using characteristics rather than direct computation.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Cayley and Hamilton, matrix in fate, satisfies its own equation, isn’t that great?
Stories
Once upon a time, there was a matrix that wanted to know about its roots. It discovered it could speak to its own polynomial – it was always satisfied by its own equation!
Memory Tools
Remember ‘C-H-C’ for Cayley-Hamilton-Theorem, where each letter relates to characteristic polynomial and matrix powers.
Acronyms
CHT
for Cayley
for Hamilton
for Theorem knowing their relationship simplifies matrix equations!
Flash Cards
Glossary
- CayleyHamilton Theorem
States that every square matrix satisfies its own characteristic equation.
- Characteristic Polynomial
Polynomial defined as p(λ) = det(A − λI).
Reference links
Supplementary resources to enhance your learning experience.
