Steps to Find Eigenvectors
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvalues and Eigenvectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start by reviewing what eigenvalues are. An eigenvalue is a scalar λ of matrix A where Av = λv for some non-zero vector v. Does that make sense?

Yes, so it represents how a matrix transforms a vector?

Exactly! Now, for each eigenvalue, we can find associated eigenvectors that point in the same direction after transformation. What do you think we need to do first to find an eigenvector?

We should substitute the eigenvalue into the equation?

Great! We substitute λ into the equation (A - λI)x = 0. Can anyone tell me why we do this?

To find where the matrix transformation is non-invertible, right?

Correct! This is how we find the null space of the matrix, which gives us the eigenvectors. Let's summarize: First, substitute, then solve.
Finding Null Space
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

After substituting, what comes next?

We have to solve (A - λI)x = 0 to find the eigenvectors, right?

Exactly! This equation is a homogeneous system, and the solutions we get are the eigenvectors. How do we solve this equation?

By row-reducing the matrix or using other methods like finding the kernel?

Very well! Row reduction will help us find the relationships between the variables in x. Remember, we are looking for non-trivial solutions.

So all the solutions together give us the eigenspace corresponding to λ.

That's right! Let's summarize: Substitute the eigenvalue, create the equation, then solve for the null space. Any clarifications needed?
Example Walkthrough
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s work through an example. If we have a matrix A and find eigenvalue λ = 3, what should we do next?

We substitute it into (A - 3I)?

Exactly! Let’s look at a specific example. Suppose A is the matrix we have: [2 1; 1 2]. What do we get when we compute (A - 3I)?

It would be [-1 1; 1 -1].

Right! Now, if we solve that matrix for (A - 3I)x = 0, can you tell me what we might find?

We will find the eigenvectors associated with λ = 3!

Exactly! And as we discussed, these eigenvectors indicate the ways in which the system changes. Remember, finding the null space allows us to see the space of solutions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section details the process for finding eigenvectors after obtaining eigenvalues, emphasizing the use of linear combinations and null space methods to derive the respective eigenvectors from the matrix's transformation properties.
Detailed
Steps to Find Eigenvectors
In this section, we explore the systematic approach to ascertain the eigenvectors corresponding to eigenvalues of a square matrix A.
Key Points:
- Substituting Eigenvalues: For each identified eigenvalue λ, we substitute λ back into the adjusted matrix equation, represented as (A − λI).
- Solving for Eigenvectors: The next step involves solving the linear homogeneous system of equations (A − λI)x = 0. The solutions to this equation yield the eigenvectors, which represent the directions in which the transformation by matrix A acts only by scaling and not by rotation.
Significance:
Understanding how to find eigenvectors is crucial in fields like civil engineering where eigenvalues can denote system responses, and eigenvectors indicate stability and mode shapes. This section builds on the foundational concepts from the previous sections and is applied in numerous structural analysis tasks.
Youtube Videos

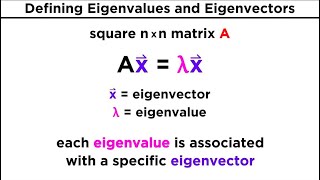


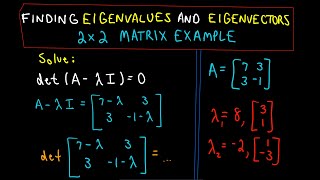





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eigenvectors
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For each eigenvalue λ:
1. Substitute λ into A−λI.
2. Solve (A−λI)x=0 to find the null space (eigenvectors).
Detailed Explanation
This section describes the steps needed to find eigenvectors associated with given eigenvalues. Once you have calculated the eigenvalue (denoted as λ), the first step is to create a new matrix by subtracting λ times the identity matrix (I) from the original matrix (A). This results in a new matrix (A−λI). Next, you set up the equation (A−λI)x=0, which is essentially looking for vectors (x) that satisfy this equation. These vectors are the eigenvectors. The equation represents a homogeneous system of equations, and the solution will give you the null space of the matrix, which consists of eigenvectors corresponding to the eigenvalue λ.
Examples & Analogies
Think of eigenvectors like your specific dance moves corresponding to unique songs (eigenvalues). Once you identify the song (eigenvalue), you need to find which specific moves (eigenvectors) fit perfectly with it. The process of finding those moves involves listening to the music (constructing (A−λI)) and figuring out what works (solving for x in (A−λI)x=0). Just like certain moves will only work for the specific rhythm and tunes of a song, certain eigenvectors correspond only to specific eigenvalues.
Substituting λ into the Matrix
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Substitute λ into A−λI.
Detailed Explanation
To find the eigenvectors, the first step is to replace λ in the equation A−λI. This means taking the computed eigenvalue and using it in the equation by subtracting λ times the identity matrix from A. By substituting λ, we're transforming the original matrix into a new matrix that contains the relationship defined by that eigenvalue. This step is crucial because it directs us towards finding the vectors that are stretched or scaled by this eigenvalue.
Examples & Analogies
Imagine you’re adjusting a recipe (matrix A) by taking out a certain ingredient that represents the eigenvalue (λ). When you remove that ingredient (substitute λ), you end up with a new version of the dish (A−λI) that you are trying to refine. You then see how the changes to your ingredients affect the final outcome, which parallels how substituting λ into the matrix shapes the solutions we seek (the eigenvectors).
Solving for Eigenvectors
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Solve (A−λI)x=0 to find the null space (eigenvectors).
Detailed Explanation
After substituting λ into A−λI, the next step is to solve the equation (A−λI)x=0. This equation is a homogeneous system of linear equations where we seek non-zero solutions for the vector x. The solutions to this equation form the null space of the matrix (A−λI). The null space is significant because it contains all the eigenvectors corresponding to the eigenvalue λ. In linear algebra, the nontrivial solutions represent the directions in which the original space (transformed by A) does not change under the transformation represented by λ.
Examples & Analogies
Think of this process like finding the right key (eigenvector) that opens a specific lock (the transformation defined by A). Once you've created the lock (A−λI) by substituting your key code (λ), you will test various keys (solving for x) until you find the one that actually opens it (solves the equation). This represents the specific vectors that maintain their direction when plugged into the transformation process defined by the eigenvalue.
Key Concepts
-
Eigenvalue: A scalar that signifies the scaling factor of the eigenvector during matrix transformation.
-
Eigenvector: A vector whose direction remains unchanged under transformation, only scaled by the eigenvalue.
-
Substitution Step: The process of plugging in the eigenvalue into (A - λI) to form a new matrix.
-
Finding Null Space: The method used to determine the set of eigenvectors corresponding to a given eigenvalue.
Examples & Applications
For matrix A = [2 1; 1 2], the eigenvalues found are λ = 1 and λ = 3. Substituting λ = 1 gives us (A - λI) resulting in a system we solve for eigenvectors.
For λ = 3, we similarly find eigenvectors associated, which leads to the description of the system's transformation.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find vectors of eigen, substitute first; then solve for the null, let solutions burst.
Stories
Imagine a traveler (the eigenvector) who multiplies their speed (the eigenvalue) when passing through a tunnel (the matrix), but their path stays the same; they only fast-track through.
Memory Tools
S-N-S: Substitute - Nullspace - Solve for eigenvalues and their vectors.
Acronyms
SVE
Substitute
Vectorize
and Eigen-finding to remember the process.
Flash Cards
Glossary
- Eigenvalue
A scalar λ such that there exists a non-zero vector x satisfying the equation Ax = λx.
- Eigenvector
A non-zero vector that only changes by a scalar factor when a linear transformation is applied.
- Null Space
The set of all vectors x such that Ax = 0; used to find eigenvectors.
- Homogeneous System
A system of linear equations that is set equal to zero.
Reference links
Supplementary resources to enhance your learning experience.
